

From the Privacy experts corner. Intelligence Collective. Podcast science 126 – L’Impensable Hasard: la téléportation quantique avec Nicolas Gisin. Rating: 4.8/5 (5 votes cast) L’intro de Nicotupe Nicolas Gisin présente dans son livre un concept que je ne connaissais personnellement pas : l’intrication quantique. Bien comprendre ce que c’est et pourquoi c’est révolutionnaire (oui, vous m’avez convaincu M. Gisin) n’est pas chose facile et je vais tenter ici une brève explication. “Intrication” “quantique”, deux mots peu simples. Commençons par quantique : on en a déjà parlé ici. Le concept d’intrication seul va vous paraître simpliste. On en arrive alors au sujet de ce livre, l’intrication quantique.
Nicolas Gisin. Le livre de Nicolas Gisin prend un long moment à expliquer ce nouveau concept par le biais d’un jeu, le jeu de Bell, où l’on ne peut pas gagner sans intrication. Intrication quantique. Thèmes - Physique quantique. How to Fall in Love With Math. Rectangle World – HTML5 Canvas and JavaScript: Tutorials and Experiments. Making the Paper Snowflake Web App, Part 1 – Layering canvases Published on December 31, 2013 My first blog post explaining some of the code behind my Paper Snowflake web app.
In this installment, we look at how multiple canvases are used together to handle drawing and interactivity tasks. Read more… Paper Snowflake Maker – Create, save, and share snowflakes with this HTML5 Canvas app. Published on December 12, 2013 Create virtual paper snowflakes with this web app built around the HTML5 canvas. Read more… N-body planar choreographies: illustrating mathematics in HTML5 canvas Published on August 20, 2013 An application built in HTML5 and canvas is used to illustrate some intriguing mathematics. Read more… Dithered gradients for Processing. Published on July 29, 2013 I share some code that you can use in Processing applications to create linear and radial gradients.
Figures for "Impossible fractals" Figures for "Impossible fractals" Cameron Browne.

Archery. Symétries et morphogenèse. Fractales sur Google Earth. Written by Paul Bourke Started: October 2010.

Last updated: October 2012 Introduction The following is a "photographic" gallery of fractal patterns found while exploring the planet with Google Earth. Each is provided with a KMZ file so the reader can explore the region for themselves. Readers are encouraged to submit their own discoveries for inclusion, credits will be included. Self Similarity Fractals are usually associated with self similarity across scales. An example of this for a river system is illustrated below [KMZ file], clicking on an image will give the high resolution version of the image without the markings.
Another way to think about whether something exhibits self similarity is if it can be interpreted to exist at different scales. Système d'unités pifométriques. Beauté et esthétique mathématique. Simon Diner Il faut se garder du hasard comme du calcul Peter MONDRIAN Deux choses menacent le monde, l’ordre et le désordre.

Ce que je cherche avant tout est l’expression Henri MATISSE Le problème des rapports entre beauté, harmonie et propriétés mathématiques a été largement posé et illustré dans l'Antiquité. Le rôle, contesté ou non, du nombre d'or, l'utilisation des tracés régulateurs par les peintres, les problèmes de la perspective, et la pratique et la théorie de l'architecture sont les manifestations les plus connues de recettes mathématiques pour l'obtention de la beauté. Il y a là un immense domaine où l'art et la mathématique se côtoient, s'observent, se fécondent mutuellement. Brillamment illustrée par Albrecht Dürer et Leonardo da Vinci cette synergie entre art et science va souffrir de l'isolement progressif des deux domaines, au point de ne pas constituer aujourd'hui une zone bien explorée et bien intégrée de la culture. L’esthétique n’est pas seulement l’étude de la beauté.
L'esthétique en mathématiques. Wiki : Beauté mathématique. Un article de Wikipédia, l'encyclopédie libre.
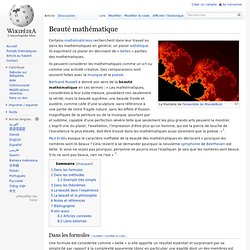
Certains mathématiciens recherchent dans leur travail ou dans les mathématiques en général, un plaisir esthétique. Ils expriment ce plaisir en décrivant de « belles » parties des mathématiques. Ils peuvent considérer les mathématiques comme un art ou comme une activité créative. Des comparaisons sont souvent faites avec la musique et la poésie. Bertrand Russell a donné son sens de la beauté mathématique en ces termes : « Les mathématiques, considérées à leur juste mesure, possèdent non seulement la vérité, mais la beauté suprême, une beauté froide et austère, comme celle d'une sculpture, sans référence à une partie de notre fragile nature, sans les effets d'illusion magnifiques de la peinture ou de la musique, pourtant pur et sublime, capable d'une perfection sévère telle que seulement les plus grands arts peuvent la montrer.
Dans les formules[modifier | modifier le code] Un exemple de belle formule est celle de Leonhard Euler.