

Table de constantes mathématiques. Un article de Wikipédia, l'encyclopédie libre.
Cet article donne une liste de certaines constantes mathématiques. Typiquement, une constante en mathématique est un nombre réel ou complexe. À la différence des constantes physiques, les constantes mathématiques sont définies indépendamment de toute mesure physique et apparaissent dans divers contextes. Liste[modifier | modifier le code] Notes[modifier | modifier le code] Intervalle [0,1][modifier | modifier le code] Constantes réelles comprises entre 0 et 1.
Constantes mathématiques (représentées en fraction continuée) E (nombre) Un article de Wikipédia, l'encyclopédie libre.
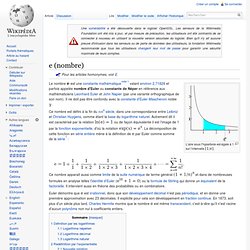
Pour les articles homonymes, voir E. L’aire sous l’hyperbole est égale à 1 sur l’intervalle [1;e]. Euler démontre que e est irrationnel, donc que son développement décimal n'est pas périodique, et en donne une première approximation avec 23 décimales. Il explicite pour cela son développement en fraction continue.
Pi. Un article de Wikipédia, l'encyclopédie libre.
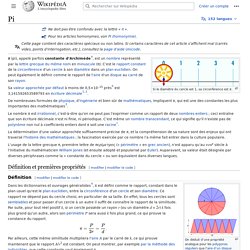
Cette page contient des caractères spéciaux. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode. Si le diamètre du cercle est 1, sa circonférence est π. Sa valeur approchée par défaut à moins de 0,5×10–15 près[2] est 3,141 592 653 589 793 en écriture décimale[3],[4]. De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques[5]. Le nombre π est irrationnel, c’est-à-dire qu’on ne peut pas l’exprimer comme un rapport de deux nombres entiers ; ceci entraîne que son écriture décimale n’est ni finie, ni périodique. La détermination d’une valeur approchée suffisamment précise de π, et la compréhension de sa nature sont des enjeux qui ont traversé l’histoire des mathématiques ; la fascination exercée par ce nombre l’a même fait entrer dans la culture populaire.
Nombre d'or. La proportion définie par a et b est dite d'« extrême et moyenne raison » lorsque a est à b ce que a + b est à a, soit : lorsque (a + b)/a = a/b. Le rapport a/b est alors égal au nombre d'or. Le nombre d'or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l'unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b), ce qui s'écrit : Le découpage d'un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en « extrême et moyenne raison ».
Constante de Gauss. Un article de Wikipédia, l'encyclopédie libre.
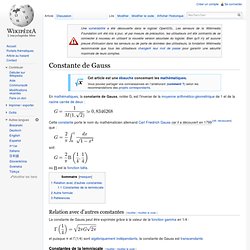
Cette constante porte le nom du mathématicien allemand Carl Friedrich Gauss car il a découvert en 1799[réf. nécessaire] que : Constante de Khintchine. Un article de Wikipédia, l'encyclopédie libre. En théorie des nombres, la constante de Khintchine est la valeur de la moyenne géométrique que prennent l'infinité des dénominateurs du développement de la fraction continue d'un nombre réel, qui est identique pour presque tous les nombres réels. C'est un résultat démontré par Alexandre Khintchine[1]. Il est donc presque toujours vrai que, pour on a[2] : Parmi les nombres x dont le développement n'a pas cette propriété se trouvent les nombres rationnels, les solutions des équations quadratiques à coefficients rationnels (incluant le nombre d'or), et le nombre e. Parmi les nombres dont le développement en fraction continue semble avoir cette propriété (d'après des études numériques), figurent les nombres π, γ, et la constante de Khintchine elle-même.
Nombres de Feigenbaum. Un article de Wikipédia, l'encyclopédie libre. En mathématiques, les nombres de Feigenbaum ou constantes de Feigenbaum sont deux nombres réels découverts par le mathématicien Mitchell Feigenbaum en 1975. Tous deux expriment des rapports apparaissant dans les diagrammes de bifurcation de la théorie du chaos. Exemple de diagramme de bifurcation. La première constante de Feigenbaum est définie comme la limite du rapport entre deux intervalles successifs de la bifurcation : Elle est apparue d'abord dans le cadre de la suite logistique où , initialement étudiée par Feigenbaum ; mais il découvrit très vite que la même constante était obtenue par exemple pour la suite ; des méthodes de calcul plus élaborées permettent d'obtenir En conséquence, tout système chaotique qui obéit à cette description bifurquera à la même vitesse.
Auto-similarité de l'ensemble de Mandelbrot près du point de Feigenbaum -1,401155 ; le facteur d'agrandissement d'un cycle au suivant est la constante ou (en) Eric W. Constante d'Euler-Mascheroni. Un article de Wikipédia, l'encyclopédie libre. Définition[modifier | modifier le code] La constante d'Euler-Mascheroni est définie comme étant : ou, de façon condensée : Constante de Brun. Un article de Wikipédia, l'encyclopédie libre. Cette constante tire son nom du mathématicien Viggo Brun qui démontra en 1919 que cette série est convergente[1]. Définition[modifier | modifier le code] Soit , etc. la suite des sommes partielles des inverses des premiers termes de la suite précédente : À la différence de la série des inverses de tous les nombres premiers qui, elle, diverge, cette série est convergente.