

Systèmes logiques formels) Dernière mise à jour de ce chapitre: 2014-04-06 20:43:38 | {oUUID 1.794} Version: 2.2 Révision 4 | Rédacteur: Vincent ISOZ | Avancement: ~80% vues depuis le 2012-01-01: 0 Le lecteur connaissant bien l'objectif de ce site ne doit pas s'attendre à voir ici de quelconques schémas de boutons poussoirs, interrupteurs, chronogrammes ou encore de schémas électriques de norme MIL ou autres.
Nous resterons donc dans un cadre purement formel des systèmes logiques et de leurs outils. Définitions: D1. D2. Remarque: Nous différencions la "logique stricte" de la "logique floue" qui seront toutes deux définies dans les détails plus loin. Considérons dans un premier temps un ensemble que nous noterons B à deux éléments (plus formellement notés D1.
D2. Dans B. Une valeur D3. Cet énoncé prend généralement la forme d'un tableau à n+1 colonnes et au plus lignes, chaque ligne exposant une combinaison des variables et la valeur correspondante de la fonction. Vers la logique de Boole. Leibniz, comme beaucoup de savants de son époque, était à la recherche d'une manière infaillible de raisonner.
Qu'est-ce qui fausse notre raisonnement, qu'est-ce qui nous éloigne de la vérité? À l'époque de Leibniz, on répondait spontanément à cette question en accusant les sens. «Ce sont les sens qui nous trompent», avait écrit Descartes. Voilà pourquoi Leibniz, en cherchant une manière infaillible de raisonner, a été amené à s'élever dans l'abstraction jusqu'à une altitude telle que la perturbation venue des sens ne soit plus perceptible. Ce haut niveau d'abstraction est celui de la logique dite formelle. À la vérité, c'est au philosophe espagnol Raymond Lulle (1235-1315) qu'il faut remonter pour discerner l'origine d'une telle logique formelle en Occident. 1 (x) + 0 (y) = 1 (s) A l'entrée les impulsions fortes et faibles correspondent aux touches 1 et 0 que l'on frappe sur le clavier avant d'appuyer sur la fonction addition +.
Introduction à la logique mathématique. Lexique de résolution de problèmes Faire une supposition. Supposition u Faire une fausse supposition. – Stratégie de résolution de problème qui consiste à faire une hypothèse de réponse, de traiter les données en fonction de l’hypothèse et de comparer le résultat en rapport avec les données conditionnelles.

Lorsque les conditions ne sont pas vérifiées, on transforme, par exemple, le nombre par une simple proportion comme dans la règle de trois ou par d'autres opérations adéquates. Cette stratégie en est une d’enchaînement logique. Problème 1. Trouvez quatre nombres dont la somme est 194 et qui diffèrent de 5 d’un nombre voisin à l’autre. Démarche. Les nombres cherchés sont : 41, 46, 51 et 56. Nombres entiers. Nous allons commencer par parler des nombres entiers.
Dans notre système de représentation décimal, nous utilisons dix chiffres pour écrire nos nombres entiers positifs : 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Prenons le nombre 1337. Le chiffre le plus à droite est le chiffre des unités, celui à côté est pour les dizaines, suivi du chiffre des centaines... Cela nous donne : Jusque là vous devez vous ennuyer, non (Enfin j'espère ! Systèmes logiques formels) Vers la logique de Boole. Eléments de logique pour l'informatique (Info 315) 1 Objectifs L’objectif du cours est de se familiariser avec un formalisme logique, la notion de démonstration, de validité, le lien entre syntaxe et sémantique.

Ce cours met en pratique un minimum d’objets mathématiques utilisés en informatique. 2 Organisation Evaluation Cours (10 séances 1h45) + TD (11 séances de 3h00) Partiel + CC + Examen final (seule une feuille A4 manuscripte recto-verso sera autorisée aux examens) Planning Cours (grand amphi) : vendredi 13 septembre 8h45-10h30 et 14h-15h45 puis vendredi 8h45-10h30 TD début semaine du 16 septembre Mardi 13h30-16h30 : Groupe 2, Alexandre Chotard, salle D201 Jeudi 13h30-16h30 : Groupe 1, Sylvain Legay, salle D201 Vendredi 13h30-16h30 : MIAGE, Véronique Ventos, salle D201 Début semaine du 9 septembre 2012 (2 cours, pas de TD) Partiel vendredi 25 octobre 2013 (bat 337 - salle 3 - places 631-720 : Examen session 1 : semaine du 16 décembre (feuille manuscripte recto-verso autorisée) Examen 2012 avec corrigéExamen session 2 : Examen 2012.
Introduction à la logique mathématique. Problème des sept ponts de Königsberg. « Problème des sept ponts de Königsberg » expliqué aux enfants par Vikidia, l’encyclopédie junior Les sept ponts de Königsberg Le problème des sept ponts de Königsberg est un problème mathématique historique résolu par Leonhard Euler grâce à sa théorie des graphes.
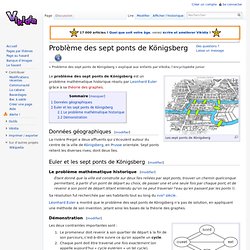
Données géographiques[modifier] La rivière Pregel a deux affluents qui s’écoulent autour du centre de la ville de Königsberg, en Prusse orientale. Sept ponts relient les diverses rives, dont deux îles. Euler et les sept ponts de Königsberg[modifier] Le problème mathématique historique[modifier] Étant donné que la ville est construite sur deux îles reliées par sept ponts, trouver un chemin quelconque permettant, à partir d'un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ (étant entendu qu'on ne peut traverser l'eau qu'en passant par les ponts !). Sa résolution fut recherchée par ses habitants tout au long du XVIIIe siècle. Démonstration[modifier]