

String Interpolation in Clojure - Chas Emerick - Muck and Brass. Patricia Tries. Longest common substring problem - Wikipedia, the free encyclope. Example[edit] The longest common substring of the strings "ABABC", "BABCA" and "ABCBA" is string "ABC" of length 3.
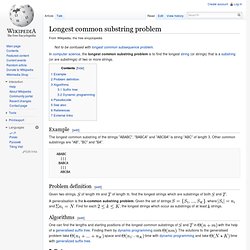
Other common substrings are "AB", "BC" and "BA". Problem definition[edit] Given two strings, of length and , find the longest strings which are substrings of both A generalisation is the k-common substring problem. , where . , the longest strings which occur as substrings of at least strings. Algorithms[edit] One can find the lengths and starting positions of the longest common substrings of in with the help of a generalised suffix tree. .
Space and time with dynamic programming and take time with generalized suffix tree. Generalised suffix tree. Suffix tree for the strings ABAB and BABA.
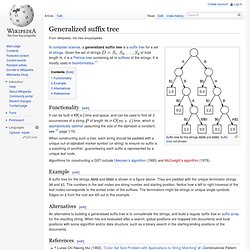
Suffix links not shown. Radix tree. In computer science, a radix tree (also patricia trie or radix trie or compact prefix tree) is a space-optimized trie data structure where each node with only one child is merged with its child.
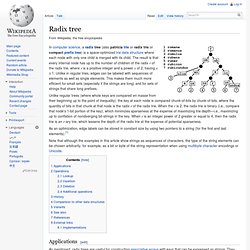
The result is that every internal node has up to the number of children of the radix r of the radix trie, where r is a positive integer and a power x of 2, having x ≥ 1. Unlike in regular tries, edges can be labeled with sequences of elements as well as single elements. This makes them much more efficient for small sets (especially if the strings are long) and for sets of strings that share long prefixes.
Ternary Search Trees. Spellchecking by computer. Roger Mitton is a lecturer in Computer Science at Birkbeck College, University of London.

His research interest is the development of a computer spellchecker for people whose spelling is poor. This article, which is a review of the methods that have been applied in computer spellchecking, is based on a chapter from his book English Spelling and the Computer, published by Longman, 1996, and now available online at Birkbeck ePrints. The article was first published in the Journal of the Simplified Spelling Society, Vol 20, No 1, 1996, pp 4-11. It is reproduced here by kind permission of the editor. By the standards of the computer industry, spelling correction has a long history; people have been writing programs to detect and correct spelling errors for over thirty years. 1. The most popular method of detecting errors in a text is simply to look up every word in a dictionary; any words that are not there are taken to be errors. 1.1 Spellcheckers without dictionaries 1.2 Saving space. Boyer-Moore-Horspool string searching.
Levenshtein distance. In information theory and computer science, the Levenshtein distance is a string metric for measuring the difference between two sequences.
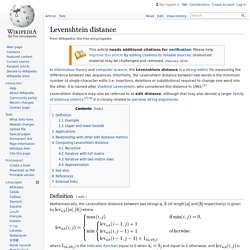
Informally, the Levenshtein distance between two words is the minimum number of single-character edits (i.e. insertions, deletions or substitutions) required to change one word into the other. It is named after Vladimir Levenshtein, who considered this distance in 1965.[1] Levenshtein distance may also be referred to as edit distance, although that may also denote a larger family of distance metrics.:32 It is closely related to pairwise string alignments. Definition[edit] Mathematically, the Levenshtein distance between two strings (of length and respectively) is given by where is the indicator function equal to 0 when and equal to 1 otherwise, and.
Knuth–Morris–Pratt algorithm. Boyer–Moore string search algorithm - Wikipedia, the free encycl. Definitions[edit] Alignments of pattern PAN to text ANPANMAN, from k=3 to k=8.
A match occurs at k=5. S[i] refers to the character at index i of string S, counting from 1.S[i..j] refers to the substring of string S starting at index i and ending at j, inclusive.A prefix of S is a substring S[1..i] for some i in range [1, n], where n is the length of S.A suffix of S is a substring S[i..n] for some i in range [1, n], where n is the length of S.The string to be searched for is called the pattern and is referred to with symbol P.The string being searched in is called the text and is referred to with symbol T.The length of P is n.The length of T is m.An alignment of P to T is an index k in T such that the last character of P is aligned with index k of T.A match or occurrence of P occurs at an alignment if P is equivalent to T[(k-n+1)..k].
Description[edit] The Boyer-Moore algorithm searches for occurrences of P in T by performing explicit character comparisons at different alignments.