

Dr. Lubov Vassilevskaya, Home Page. 8 Bundeskanzler in 3 Minuten lernen. Körperliste - Hans Dieter Hörtrich. Denkfallen und Paradoxa. Simpsons Paradoxon (Simpson’s Paradox) In der Tabelle der Sterblichkeit aufgrund von Tuberkulose in New York und Richmond aus dem Jahre 1910 begegnet uns das Simpsonsche Paradoxon (Székely, 1990, S. 63, 75 u. 133): Widerspruch.

Bist du weiß, gehe nach Richmond. Bist du farbig, gehe ebenfalls nach Richmond. Bist du weiß oder farbig, dann bleibe in New York. Analyse. Zurück zur Übersicht Benford's Law Der Mathematiker Mark Nigrini hat ein Programm geschrieben, mit dessen Hilfe gefälschte Steuererklärungen ausfindig zu machen sind. Täglich treffen wir auf Zahlen: Zahlen, die auf der ersten Seite einer Tageszeitung stehen, Zahlen über die Größe der Binnengewässer Deutschlands, die Einwohnerzahlen der Städte oder die Familieneinkommen, die Guthaben auf den Konten einer Bank und die Zahlen in einer Steuererklärung.
Widerspruch. Das Benfordsche Gesetz. Analyse. Wer weitere Erklärungen sucht, kann beispielsweise bei Kevin Brown und Eric Weisstein nachsehen. Weitere Modelle. Da jedes Projekt ein Unikat ist, werden auch die Projektphasen individuell ausfallen.
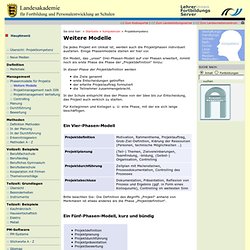
Einige Phasenmodelle stellen wir hier vor. Ein Modell, das „unser“ Drei-Phasen-Modell auf vier Phasen erweitert, nimmt noch als erste Phase die Phase der „Projektdefinition“ hinzu: In dieser Phase der Projektdefinition werden die Ziele genannt erste Entscheidungen getroffen der erteilte Projektauftrag formuliert die Teilnehmer zusammengebracht. In der Schule entspricht dies der Phase von der Idee bis zur Entscheidung, das Projekt auch wirklich zu starten. Für Kolleginnen und Kollegen u. Ein Vier-Phasen-Modell Bitte beachten Sie: Die Definition des Begriffs „Projekt“ anhand von Merkmalen ist etwas anderes als die Phase „Projektdefinition“. Ein Fünf-Phasen-Modell, kurz und bündig Quelle: MKS (Hrsg.) (1999): TO-Lehrplan Computertechnik. Dragon Dreaming. Dragon Dreaming wurde vom Australier John Croft entwickelt und ist ein effektiver Weg, um Träume oder konkrete Projektziele zu verwirklichen und gleichzeitig den Gruppengeist zu stärken.

Dragon Dreaming nutzt Wissen aus der Systemtheorie, der Organisationsentwicklung und den Weisheiten der australischen Aborigines. Die Methode unterstützt sowohl kognitives als auch intuitives Erfassen und ermöglicht dadurch eine ganzheitliche Perspektive. Die Phase der Projektentwicklung wird von einer Gruppe gemeinsam durchlaufen. Durch diesen gemeinsamen Prozess entsteht wie von selbst ein tieferes Verständnis füreinander und damit wird die kollektive Weisheit einer Gruppe zur Projektumsetzung voll nutzbar. Damit bietet Dragon Dreaming ein Werkzeug für integrales Projektmanagement. Geeignet Ablauf Der Ablauf eines Dragon Dreaming-Prozesses hängt sehr von den Wünschen des/der AuftraggeberIn sowie von den Bedürfnissen den Gruppe ab.
Einstieg Visionsfindung „Spielplan-Erstellung“ Rollen-Angebote „fast budget“ Basic Probability. Die Seite der Sprüche. Sprüchesammlung Alle Sprüche in der Reihenfolge ihres Eingangs: Sollte bei einem Spruch der Autor fehlen, dann bitte ergänzen, falls ihn jemand weiß.
Alle neu eingehenden Sprüche werden ab sofort an den Anfang der Liste gestellt. Sprüche: Sprüche, die man sich immer schon mal aufschreiben wollte. OMEGA - Schule.Medien.Materialien. Frauchavanon. Die Lernplattform. Lernpfade/Quadratische Funktionen/Die Scheitelpunkts- und Normalform und der Parameter a – DMUW. Aus den vorherigen Lerneinheiten kennst du die Eigenschaften der einzelnen Parameter.
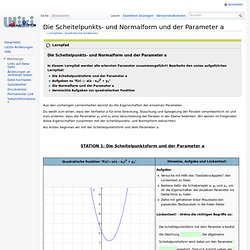
Du weißt zum einen, dass der Vorfaktor a für eine Streckung, Stauchung und Spiegelung der Parabel verantwortlich ist und zum anderen, dass die Parameter ys und xs eine Verschiebung der Parabel in der Ebene bewirken. Wir wollen im Folgenden diese Eigenschaften zusammen mit der Scheitelpunkts- und Normalform betrachten. Als erstes beginnen wir mit der Scheitelpunktsform und dem Parameter a. STATION 1: Die Scheitelpunktsform und der Parameter a Um die wichtigsten Eigenschaften aller Parameter zu wiederholen, lies das folgende Merke und überprüfe, ob dir alle Eigenschaften klar sind. Nachdem du nun dein Wissen aufgefrischt hast, kann auch gleich geübt werden! STATION 2: Aufgaben zu "f(x) a(x - xs)2 + ys" 1. Du siehst hier sowohl ein paar Graphen, als auch ein paar Funktionsvorschriften der Form "f(x) a(x - xs)2 + ys". Y = -4[x + 2]2 + 1y = [x - 2,5]2 - 1,5y = 2[x - 4]2 - 3y = [x + 3,5]2y = 5[x + 2,5]2 + 2.
Unterricht.educa.ch. Praktischer Blog zu Computereinsatz Zuletzt geändert: 25.03.2014 - 18:06 / Kommentare () Diskussions-Blog / Informatikunterricht ePilot ist der praxisbezogene Blog für Themen zum Computereinsatz im Unterricht.

Jede Woche werden auf diesem Blog hilfreiche Tipps zum Thema eLearning veröffentlicht. Halluzinogene Zuletzt geändert: 20.03.2014 - 19:26 / Kommentare () Lehrmittel / Gesundheit / Prävention / Rauschgift Informationsmaterial für Jugendliche, Lehrpersonen und Eltern, welches über Halluzinogene, deren Wirkungen und Risiken informiert. Mineralstoffe. Apps. Moodle. Materialien zum Selbstständigen Arbeiten.
Mekorlp. Deutsch.