


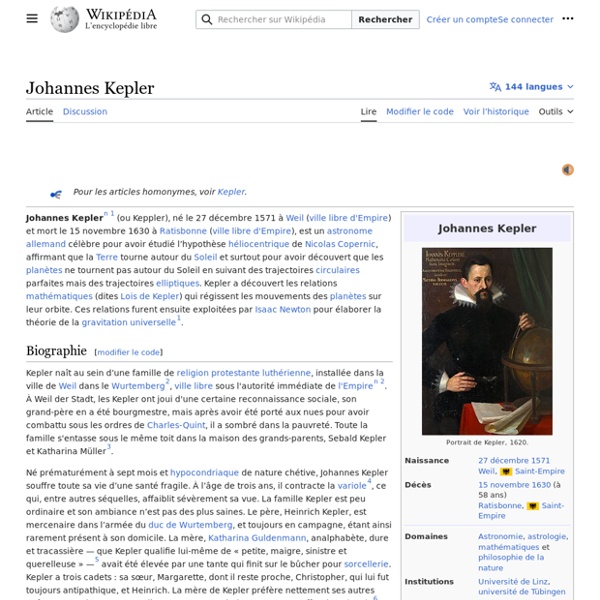
Le Songe ou l'Astronomie lunaire Le Songe ou l'Astronomie lunaire (en latin Somnium, seu opus posthumum de astronomia lunari) est un roman écrit en 1608 par Johannes Kepler et publié de manière posthume par son fils Ludwig en 1634. Le livre, écrit en latin, raconte l’histoire d’un jeune Islandais féru d’astronomie, Duracotus, dont la mère, magicienne, lui fait connaître les démons : l’un d’eux leur apprend l’existence d’une île, difficile d’accès, Levania (la Lune)… Souvent considéré comme l’un des premiers ouvrages de science-fiction, Le Songe est aussi un prétexte à une présentation des connaissances de Kepler sur l’astre lunaire. Si le Songe ne paraît que quatre ans après la mort de Kepler, en 1634, il faut cependant noter que son idée est née assez tôt dans l’esprit de l'auteur. Il est probable[P 2] que c’est aussi à cette époque que Kepler envisage de changer le genre de son récit, celui-ci étant devenu fictionnel. On peut ainsi noter que Kepler s’est refusé à écrire une utopie, malgré la mode de l’époque[P 3].
Robert Boyle Un article de Wikipédia, l'encyclopédie libre. Portrait de Robert Boyle. Robert Boyle peut être considéré comme le père de la philosophie naturelle moderne. Biographie[modifier | modifier le code] À partir de 1645, il participe à une société savante et bienfaisante qu'il appelle dans ses lettres le « collège invisible », mais dont il n'indique ni le noms des membres, ni les activités, et qui a donné lieu à diverses spéculations (en particulier comme groupe précurseur de la Royal Society). C'est à lui qu'on doit l'établissement de la Royal Society en 1663. Un legs de Robert Boyle permet la fondation en 1700, de la Boyle School, dans l'enceinte du Prieuré de Bolton, Yorkshire du Nord[2]. Travaux[modifier | modifier le code] Théologie[modifier | modifier le code] Il donna durant sa vie 300 £ par an pour la propagation de la foi en Amérique et 100 £ pour les Indes[1]. Science[modifier | modifier le code] Œuvres[modifier | modifier le code] The Sceptical Chymist (1661). Principaux ouvrages :
Biographie | Johannes Kepler - Astronome | Futura Sciences Universellement connu pour les trois lois planétaires qui portent son nom, Kepler a aussi marqué l'optique. On peut donc le considérer comme fondateur de deux branches de la science. Fils d'un bourgmestre ayant des prétentions à la noblesse, Johannes Kepler naît en 1571 à Weil der Stadt. Son père, ruiné à la suite d'une banqueroute, le retire de l'école et l'oblige à travailler dans un cabaret. Mais l'affaire ne prospère pas. Après sa formation, Kepler souhaite devenir pasteur protestant. Pendant son séjour à Graz, Kepler écrit le Mysterium Cosmographicum, mélange de copernicanisme et de mysticisme, où il postule que les dimensions du système solairesystème solaire sont parfaites. Une fois qu'il établit cette théorie, Kepler a besoin d'au moins une distance, par exemple celle de la Terre au Soleil ou de la Terre à Mars, pour calculer les autres dimensions du système solaire et obtenir ainsi le « secret du monde ». Il y a de très nombreux ouvrages, signalons uniquement ces trois :
Un voyage dans la lune au XVIIe siècle : « Le songe » de Kepler - Persée 64 UN VOYAGE DANS LA LUNE AU XVIIe SIÈCLE : Au moment où l'astronome écrit cet ouvrage, il possédait des observations précises sur la position des planètes et les mouvements de la Lune. Ue plus, ce satellite devient l'objet d'une curiosité nouvelle à partir de 1610. Jusqu'alors, on observait les astres à l'œil nu : en 1609, Galilée construisit une lunette astronomique fort puissante et fort précise pour l'époque ; elle permit au savant italien de découvrir les montagnes et les cratères de la Lune. Une ère nouvelle s'ouvrait pour l'astronomie : les savants se mirent à observer les astres avec attention. Dès 1610, au moment où Galilée publie le résultat de ses observations, Kepler en comprend toute l'importance1. Il se compose, en effet, de trois parties : un récit suivi d'une série impressionnante de notes et d'un appendice sélénogra- phique. Le Songe n'est pas différent : nous pénétrons dans un monde mystérieux. 1. 2.
Pierre Paul Rubens Signature Aidé par un atelier important, Rubens produit une œuvre considérable dans des genres divers. Il accepte de peindre un grand nombre de portraits mais, « d'instinct plus porté aux grands travaux qu'aux petites curiosités » comme il l'écrivait lui-même, il prête peu d'attention aux détails, qu'il ne peint pas en profondeur et dessine de quelques traits. Après sa naissance à Siegen, la famille s'installe à Cologne en 1578, où elle vit jusqu'à ce que Pierre Paul ait 11 ans. Beaucoup de ses tableaux représentent des sujets religieux et Rubens est d'ailleurs devenu plus tard l'une des principales voix du style pictural de la Contre-Réforme catholique[10]. En 1603, Rubens voyage en Espagne pour une mission diplomatique, apportant avec lui des cadeaux du duc de Gonzague à la Cour du roi Philippe III d'Espagne. Le sujet en est le pape Grégoire le Grand ainsi que des saints locaux majeurs adorant l'icône de la Vierge et l'Enfant. Rubens passa les dix dernières années de sa vie à Anvers.
Andreï Kolmogorov, l’Euclide du XXème siècle (Turbulence) Lorsque l’eau d’un robinet coule selon un débit parfaitement régulier, on parle d’un écoulement « laminaire ». Si le débit augmente beaucoup on voit subitement apparaître un flot turbulent. Ce phénomène de « Turbulence » produit, alors, d’innombrables tourbillons. Dans le cadre de notre partenariat avec la BNF et la Société mathématique de France, nous abordons l’extraordinaire carrière mathématique de Kolmogorov. Musique : "Concierto Fantastico" (allegro ma non troppo ) d'Isaac Albeniz"How deep is the ocean ?"
Histoire du mouvement képlérien Environ cinquante ans plus tard, la théorie sera écrite dans les Principia par Isaac Newton de fin 1684 à 1687, sous l'impulsion de son commanditaire et ami Edmond Halley. Ainsi naquit la mécanique céleste, ainsi que la mécanique rationnelle. Durant le siècle suivant, le XVIIIe, les mathématiciens ont travaillé à éclaircir cette théorie. Avant Kepler[modifier | modifier le code] Dans l'Antiquité[modifier | modifier le code] Ptolémée (90 - 168): ses travaux sur l'équant Au XVIe siècle[modifier | modifier le code] Au XVIe siècle, les scientifiques principaux qui ont étudié le mouvement des planètes sont Copernic (1543) et la "révolution copernicienne"[3]Tycho Brahe (1546 - 1601) et son "équivalence des systèmes" Les lois de Kepler, puis les lois du mouvement de Newton[modifier | modifier le code] Les autres précurseurs de Kepler de cette époque sont Les lois de Kepler (1609 - 1618) décrivent les propriétés principales du mouvement des planètes autour du Soleil. 1/. 2/. et idem en y. 3/. 4/. ). 5/.
Louis XII Louis XII, né le 27 juin 1462 au château de Blois et mort le 1er janvier 1515 à Paris, surnommé le « Père du peuple » par les états généraux de 1506, est roi de France de 1498 à 1515. Au moment du mariage de sa fille et du futur Louis XII, Louis XI aurait cyniquement glissé à l'un de ses confidents « […] pour ce qu'il me semble que les enfants qu'ils auront ensemble ne leur coûteront point cher à nourrir […] ». Ce mariage est vécu par Louis d'Orléans comme un affront. À la mort de Louis XI, il échoue à obtenir la régence aux états généraux de Tours, confiée à Anne de Beaujeu. À cette occasion, se référant aux droits hérités de sa grand-mère Valentina Visconti, il tenta de conquérir le duché de Milan, affaibli par une crise économique, et le 11 juin 1495, il occupa avec ses troupes la ville de Novare, qui lui fut donnée pour trahison. Le 7 avril 1498, Charles VIII meurt accidentellement, sans enfant survivant. Aile Louis XII du château de Blois (1498-1503).
Andreï Kolmogorov Andreï Nikolaïevitch Kolmogorov Andreï Nikolaïevitch Kolmogorov (en russe : Андрей Николаевич Колмогоров Écouter ; 25 avril 1903 à Tambov – 20 octobre 1987 à Moscou) est un mathématicien russe et soviétique qui a apporté des contributions significatives en mathématiques, notamment en théorie des probabilités, topologie, turbulence, mécanique classique, logique intuitionniste, théorie algorithmique de l'information et en analyse de la complexité des algorithmes[1],[2],[3]. Biographie[modifier | modifier le code] Enfance[modifier | modifier le code] Kolmogorov est né à Tambov en 1903. Sa mère Maria Iakovlevna Kolmogorova (1871-1903), célibataire, meurt en accouchant. Sa tante Vera Yakovlevna Kolmogorova[n 1] l'adopte et déménage en 1910 avec lui à Moscou, où il commence à étudier à l'institut privé Repman[n 2]. Études et premiers résultats[modifier | modifier le code] Carrière[modifier | modifier le code] En 1931, il reçoit une chaire de professeur à l'université de Moscou[11].
Jacques Rueff Jacques Rueff en 1938. signature Vue de la sépulture. Jacques Léon Rueff, né le 23 août 1896 à Paris et mort le 23 avril 1978 dans la même ville, est un haut fonctionnaire et économiste français, qui a joué un rôle majeur dans les politiques économiques menées dans les années 1930 et surtout à partir de 1958. Il participe à plusieurs réformes économiques en France : en 1926-1928 auprès de Raymond Poincaré pour rétablir le franc, en 1938 auprès de Paul Reynaud, et surtout auprès du général de Gaulle en 1958-1960, où il joue un rôle majeur dans la conception d'un plan d'assainissement financier, qui sera mis en œuvre par Antoine Pinay : le plan Pinay-Rueff, puis en concevant un plan de « suppression des obstacles à l'expansion économique » au sein du comité Rueff-Armand. Libéral, proche des idées de l'École autrichienne, il s'est fermement opposé aux idées keynésiennes, qui sont remises en cause avec la crise et la stagflation des années 1970. Biographie[modifier | modifier le code]
Jovan Karamata Un article de Wikipédia, l'encyclopédie libre. Biographie[modifier | modifier le code] Plaque commémorative, à Zemun. Jovan Karamata est né à Zagreb le 1er février 1902. Ses ascendants sont des Aroumains. Il séjourné à Paris en 1927-1928 comme boursier de la fondation Rockefeller, et en 1928 devient assistant de mathématiques à la faculté de philosophie de l'université de Belgrade. Il devient membre de l'Académie croate des sciences et des arts en 1933, de la Société royale des sciences de Bohême en 1936, et de l’Académie royale de Serbie en 1939 et membre de l'Académie serbe des sciences et des arts en 1948. Karamata était membre des sociétés mathématiques suisse, française et allemande et a été, en 1954, secrétaire du journal L'Enseignement mathématique à Genève. Karamata meurt à Genève le 14 août 1967. Travaux[modifier | modifier le code] Karamata a publié 122 articles scientifiques, 15 monographies et manuels, et 7 articles pédagogiques[3]. Bibliographie[modifier | modifier le code]
Dragonnades Le « dragon missionnaire » : « Qui peut me résister est bien fort ». Dans les faits, ce ne sont pas toujours des dragons qui effectuèrent les dragonnades antiprotestantes. Chronologie des dragonnades[modifier | modifier le code] 1681-1686[modifier | modifier le code] 1744-1759[modifier | modifier le code] du 20 décembre 1744 au 1er mai 1745 : dragonnades à Millau et dans le Rouergue.1758 : dragonnades en Béarn (Orthez, Salies et Bellocq) et en Guyenne (Sainte-Foy, Bregerac, Tonneins et Clairac), à Jonzac, le Louis, Segonzac.1759 : dragonnades à Chez-Piet. Nombre de conversions obtenues (années 1680)[modifier | modifier le code] Histoire[modifier | modifier le code] Les « missions bottées » de Louvois (1681)[modifier | modifier le code] René de Marillac, l'intendant du Poitou, ordonna de contrôler le rôle des tailles et de marquer les réformés dans la marge afin de les « grever », tant pour l'impôt que pour le logement des gens de guerre. Les dragonnades de Louis XV[modifier | modifier le code]
Kronecker, entre innovation et refus des nouveautés Leopold Kronecker naît le 7 décembre 1823 en Pologne, à Legnica (qui s'appelait à l'époque Liegnitz). Issu d'une famille aisée (son père Isidor Kronecker est un homme d'affaires et sa mère Johanna Prausnitzer est également riche), il entre au lycée où il est élève de Kümmer qui le forme aux sciences. Kronecker poursuit des études d'astronomie, de chimie, de météorologie et de philosophie dans plusieurs universités : Berlin (1841) puis Bonn (été 1843), Breslau (hiver 1843-1844, Kümmer avait été nommé dans cette ville en 1842) et à nouveau Berlin. Il soutient une thèse le 14 août 1845 sous la direction de Dirichlet. Mais il arrête ici ses études pour se consacrer aux affaires familiales. Il rentre à Legnica et se marie avec Fanny Prausnitzer, une de ses cousines. Malgré son refus de certaines idées, comme l'existence des nombres transcendants, la théorie des ordinaux transfinis (Cantor) ou la construction des réels de Weierstrass, il fut l'un des premiers à comprendre Galois.