http://www.numberspiral.com/index.html
Frequency of Primes Frequency of Primes Tags: prime , primes , visualization Categories: Color Theory , Data Visualization , Education , Featured , Programming Project Summary How often do prime numbers occur within a list of integers? How Mathematics Can Make Smart People Dumb - Ben O'Neill Mathematics can sometimes make smart people dumb. Let me explain what I mean by this. I don't mean that it is dumb not to be good at mathematics. After all, mathematics is a highly abstract and challenging discipline requiring many years (decades even) of study, and there are plenty of very smart people who have little understanding of it, and little ability to use it.
Excel, a Presentation Platform? - Excel Hero Blog Presentation authoring is dead simple in PowerPoint. It definitely has its merits. But have you ever noticed that most presentations are similar, and frankly boring. Prime Integer Observatory This application illustrates the notion of an integer?s factors, and of the related property of integers called primeness, or primality. An integer is called prime if it is the product of only one distinct pair of integers. Hammack Home This book is an introduction to the standard methods of proving mathematical theorems. It has been approved by the American Institute of Mathematics' Open Textbook Initiative. Also see the Mathematical Association of America Math DL review (of the 1st edition), and the Amazon reviews. The second edition is identical to the first edition, except some mistakes have been corrected, new exercises have been added, and Chapter 13 has been extended. (The Cantor-Bernstein-Schröeder theorem has been added.) The two editions can be used interchangeably, except for the last few pages of Chapter 13.
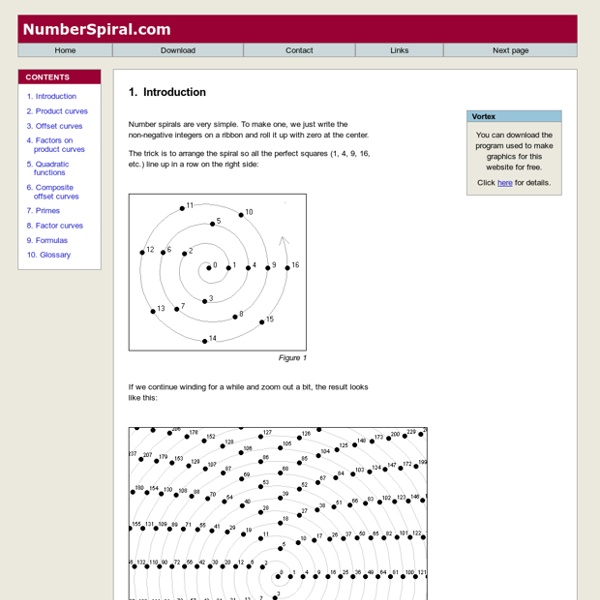
Ulam spiral Do you see any pattern in this graph? You will not believe at first glance that it is generated using prime numbers. In order to generate it, the numbers are arranged in a spiral, as follows: Mathematical Sculptures Made Out Of Office Supplies (PHOTOS) "I think about math constantly and I see and look for math in everything around me." Zachary Abel is a second year Ph.D student in the MIT Mathematics department, but he also creates sculptures out of everyday objects. "By transforming often-overlooked household items into elaborate, mathematical sculptures, I hope to share this sense of excitement, curiosity, and beauty that a mathematical outlook has instilled in me." Zachary Abel, "Impenetraball", 2011. The "Impenetraball" protects its hollow interior with a dense, chainmail-like mesh made from 132 binder clips (and pliers).
Curtis Macdonald Here are the template files I use in order to create the experimental tonal system using the 3-digit Lo Shu or “solfeggio” number series as illustrated in the above image (courtesy of Bob Philips). For all related posts, click here. These numbers are interpreted as frequencies in Hz, and are inspired by the following threads. Although these numeric concepts are rather ancient, the frequencies themselves are not. The 81 Lo Shu Tones within the 729 Fabric I used the software Custom Scale Editor (CSE) for creating these scales.
Primal Chaos The image shows a random multiple of 6 at "6k". In order to have twin primes we cannot have any circle intersecting adjacently to 6k (obviously). Let's see how this happens: Please note that the reason I'm only using prime numbers for this is because we only need prime numbers. For example, the 9 is not needed because it is a multiple of 3 (3 is prime and can only fall on 6k). Same with 15, 21, 27 and so on (which are also multiples of 3). Euler's identity The exponential functionez can be defined as the limit of (1 + z/N)N, as N approaches infinity, and thus eiπ is the limit of (1 +iπ/N)N. In this animation N takes various increasing values from 1 to 100. The computation of (1 + iπ/N)N is displayed as the combined effect of N repeated multiplications in the complex plane, with the final point being the actual value of (1 +iπ/N)N. It can be seen that as N gets larger (1 +iπ/N)N approaches a limit of −1. where i is the imaginary unit, which satisfies i2 = −1, and
American Five-Sided Pyramid 3 (David’s Key) « Sacred geometry As I already mentioned, „Behind the hill is even higher second hill. “ Going through this geometric way and superficially observing, occures a situation that I could call „confusion“. Nobody likes that condition, and the only solution is to analyze mysteries (hills) more closely. Sometimes, the cause oft hat condition is the haste. In that way theories, or you can call them stories, occures. Uncertainties that may lead to resignation, which should notbe a placeat this stage of technological development of the human race. Technology- helps in resolving issues which we are and why we are.
That is all I require: Building Numbers Caution: Distraction ahead. Summary: Visualizations of Ulam Spirals. Recently a brief discussion evolved into an hour of visualizations of the compositeness of numbers. A number that is the power of a prime seems to be closer to a prime than a number that has lots of prime factors. ω(n) is the number of distinct prime factors of n, a notion which is used here and there. How to visualize the compositeness of a number? Augustin-Louis Cauchy Baron Augustin-Louis Cauchy (French: [oɡystɛ̃ lwi koʃi]; 21 August 1789 – 23 May 1857) was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors. He defined continuity in terms of infinitesimals, almost singlehandedly founded complex analysis and initiated the study of permutation groups in abstract algebra. A profound mathematician, Cauchy exercised a great influence over his contemporaries and successors.
GEOMETRIC DESIGNS OF THE GRANITE The following is my proposal to demonstrate that the granite leaf slabs and its carved boss over the north side of the upper section, are a result of the same type of geometric pattern configuration, and that this configuration corresponds to the configuration I suggested for the solution of the Great Pyramid's geometry in my previous posts, and to design, build, and seal the antechamber. The shape and dimensions of the boss are shown below: The boss was defined by Sir W. Petrie to be a rough carving over the side of the granite leaf stone, as other similar carvings over the sides of the stone blocks, used to handle and manipulate these stones blocks for the building of pyramids, tombs and temples. My idea, for many years, is that this particular object do not represents a working boss. To apply a label of a working boss, because all bosses are carved over the stone surfaces in a similar way, is not enough for me to conclude that this is a working boss.