Electromagnetic induction Electromagnetic induction is the production of a potential difference (voltage) across a conductor when it is exposed to a varying magnetic field. It is described mathematically by Faraday's law of induction, named after Michael Faraday who is generally credited with the discovery of induction in 1831. History[edit] A diagram of Faraday's iron ring apparatus. Electromagnetic induction was discovered independently by Michael Faraday and Joseph Henry in 1831; however, Faraday was the first to publish the results of his experiments.[2][3] In Faraday's first experimental demonstration of electromagnetic induction (August 29, 1831[4]), he wrapped two wires around opposite sides of an iron ring or "torus" (an arrangement similar to a modern toroidal transformer). Faraday explained electromagnetic induction using a concept he called lines of force. Faraday's law and the Maxwell–Faraday equation[edit] where is the electromotive force (EMF) and ΦB is the magnetic flux. the EMF on a wire loop is:
Diffraction Diffraction pattern of red laser beam made on a plate after passing a small circular hole in another plate Diffraction refers to various phenomena which occur when a wave encounters an obstacle or a slit. In classical physics, the diffraction phenomenon is described as the apparent bending of waves around small obstacles and the spreading out of waves past small openings. These characteristic behaviors are exhibited when a wave encounters an obstacle or a slit that is comparable in size to its wavelength. Similar effects occur when a light wave travels through a medium with a varying refractive index, or when a sound wave travels through a medium with varying acoustic impedance. Diffraction occurs with all waves, including sound waves, water waves, and electromagnetic waves such as visible light, X-rays and radio waves. Richard Feynman[3] wrote: The formalism of diffraction can also describe the way in which waves of finite extent propagate in free space. Examples[edit] History[edit] where
Observable universe The surface of last scattering is the collection of points in space at the exact distance that photons from the time of photon decoupling just reach us today. These are the photons we detect today as cosmic microwave background radiation (CMBR). However, with future technology, it may be possible to observe the still older relic neutrino background, or even more distant events via gravitational waves (which also should move at the speed of light). Sometimes astrophysicists distinguish between the visible universe, which includes only signals emitted since recombination—and the observable universe, which includes signals since the beginning of the cosmological expansion (the Big Bang in traditional cosmology, the end of the inflationary epoch in modern cosmology). The Universe versus the observable universe[edit] If the Universe is finite but unbounded, it is also possible that the Universe is smaller than the observable universe. Size[edit] Misconceptions on its size[edit] Horizons[edit]
Electromagnetic field The field can be viewed as the combination of an electric field and a magnetic field. The electric field is produced by stationary charges, and the magnetic field by moving charges (currents); these two are often described as the sources of the field. The way in which charges and currents interact with the electromagnetic field is described by Maxwell's equations and the Lorentz force law. From a classical perspective in the history of electromagnetism, the electromagnetic field can be regarded as a smooth, continuous field, propagated in a wavelike manner; whereas from the perspective of quantum field theory, the field is seen as quantized, being composed of individual particles.[citation needed] Structure of the electromagnetic field[edit] The electromagnetic field may be viewed in two distinct ways: a continuous structure or a discrete structure. Continuous structure[edit] Classically, electric and magnetic fields are thought of as being produced by smooth motions of charged objects.
Laser Red (660 & 635 nm), green (532 & 520 nm) and blue-violet (445 & 405 nm) lasers Among their many applications, lasers are used in optical disk drives, laser printers, and barcode scanners; fiber-optic and free-space optical communication; laser surgery and skin treatments; cutting and welding materials; military and law enforcement devices for marking targets and measuring range and speed; and laser lighting displays in entertainment. Fundamentals Lasers are characterized according to their wavelength in a vacuum. Terminology Laser beams in fog, reflected on a car windshield The word laser started as an acronym for "light amplification by stimulated emission of radiation". A laser that produces light by itself is technically an optical oscillator rather than an optical amplifier as suggested by the acronym. Design Components of a typical laser: 1. Animation explaining the stimulated emission and the laser principle Laser physics Stimulated emission Gain medium and cavity The light emitted History
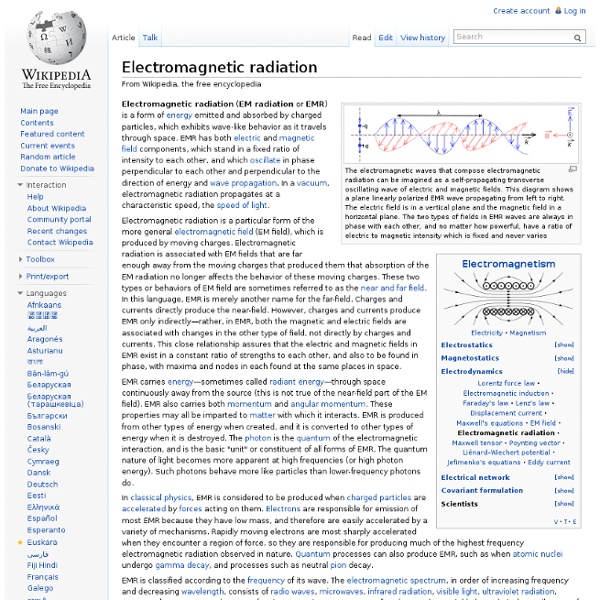
Electromagnetic field Electric and magnetic fields produced by moving charged objects The field can be viewed as the combination of an electric field and a magnetic field. The electric field is produced by stationary charges, and the magnetic field by moving charges (currents); these two are often described as the sources of the field. The way in which charges and currents interact with the electromagnetic field is described by Maxwell's equations and the Lorentz force law.[2] A sinusoidal electromagnetic wave propagating along the positive z-axis, showing the electric field (blue) and magnetic field (red) vectors. Structure[edit] The electromagnetic field may be viewed in two distinct ways: a continuous structure or a discrete structure. Continuous structure[edit] Classically, electric and magnetic fields are thought of as being produced by smooth motions of charged objects. Discrete structure[edit] The electromagnetic field may be thought of in a more 'coarse' way. Dynamics[edit] Feedback loop[edit] Gauss's law
Electrical resistance An object of uniform cross section has a resistance proportional to its resistivity and length and inversely proportional to its cross-sectional area. All materials show some resistance, except for superconductors, which have a resistance of zero. The resistance (R) of an object is defined as the ratio of voltage across it (V) to current through it (I), while the conductance (G) is the inverse: may be most useful; this is called the "differential resistance". Introduction[edit] The hydraulic analogy compares electric current flowing through circuits to water flowing through pipes. In the hydraulic analogy, current flowing through a wire (or resistor) is like water flowing through a pipe, and the voltage drop across the wire is like the pressure drop that pushes water through the pipe. The voltage drop (i.e., difference in voltage between one side of the resistor and the other), not the voltage itself, provides the driving force pushing current through a resistor. Ohm's law[edit] where .
Polarization (waves) Circular polarization on rubber thread, converted to linear polarization Polarization (also polarisation) is a property of waves that can oscillate with more than one orientation. Electromagnetic waves such as light exhibit polarization, as do some other types of wave, such as gravitational waves. Sound waves in a gas or liquid do not exhibit polarization, since the oscillation is always in the direction the wave travels. The most common optical materials (such as glass) are isotropic and simply preserve the polarization of a wave but do not differentiate between polarization states. Polarization is an important parameter in areas of science dealing with transverse wave propagation, such as optics, seismology, radio, and microwaves. Most sources of light are classified as incoherent and unpolarized (or only "partially polarized") because they consist of a random mixture of waves having different spatial characteristics, frequencies (wavelengths), phases, and polarization states. and . ).
Energy Property that makes changes possible Common forms of energy include the kinetic energy of a moving object, the potential energy stored by an object (for instance due to its position in a field), the elastic energy stored in a solid object, chemical energy associated with chemical reactions, the radiant energy carried by electromagnetic radiation, and the internal energy contained within a thermodynamic system. All living organisms constantly take in and release energy. Due to mass–energy equivalence, any object that has mass when stationary (called rest mass) also has an equivalent amount of energy whose form is called rest energy, and any additional energy (of any form) acquired by the object above that rest energy will increase the object's total mass just as it increases its total energy. Human civilization requires energy to function, which it gets from energy resources such as fossil fuels, nuclear fuel, or renewable energy. Forms History Units of measure Scientific use Chemistry Biology
Permittivity A dielectric medium showing orientation of charged particles creating polarization effects. Such a medium can have a higher ratio of electric flux to charge (permittivity) than empty space In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how much electric field (more correctly, flux) is 'generated' per unit charge in that medium. More electric flux exists in a medium with a high permittivity (per unit charge) because of polarization effects. In SI units, permittivity ε is measured in farads per meter (F/m); electric susceptibility χ is dimensionless. where εr is the relative permittivity of the material, and ε0 = 8.8541878176.. × 10−12 F/m is the vacuum permittivity. Explanation[edit] Vacuum permittivity[edit] Its value is[1] where If
Spectral line Continuous spectrum Absorption lines for air, under indirect illumination, with the direct light source not visible, so that the gas is not directly between source and detector. Here, Fraunhofer lines in sunlight and Rayleigh scattering of this sunlight is the "source." This is the spectrum of a blue sky somewhat close to the horizon, pointing east at around 3 or 4 pm (i.e., Sun in the West) on a clear day. A spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies. Types of line spectra[edit] Spectral lines are the result of interaction between a quantum system (usually atoms, but sometimes molecules or atomic nuclei) and a single photon. Depending on the type of gas, the photon source and what reaches the detector of the instrument, either an emission line or an absorption line will be produced. Nomenclature[edit] Natural broadening[edit]
Gravity Attraction of masses and energy In physics, gravity (from Latin gravitas 'weight'[1]) is a fundamental interaction which causes mutual attraction between all things that have mass. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the strong interaction, 1036 times weaker than the electromagnetic force and 1029 times weaker than the weak interaction. As a result, it has no significant influence at the level of subatomic particles.[2] However, gravity is the most significant interaction between objects at the macroscopic scale, and it determines the motion of planets, stars, galaxies, and even light. On Earth, gravity gives weight to physical objects, and the Moon's gravity is responsible for sublunar tides in the oceans (the corresponding antipodal tide is caused by the inertia of the Earth and Moon orbiting one another). Definitions History Ancient world In the ancient Middle East, gravity was a topic of fierce debate. Specifics