


TPE : Le nombre d'or dans la nature, ou et pourquoi ? A.Croissance des plantes et Fibonacci - B. Phyllotaxie - C. Quelques exemples de plantes C).Quelques exemples de plantes ou l'on retrouver phi On retrouve un peu partout j dans la nature, grâce au nombres de la suite de Fibonacci. L’ananas. On le retrouve ainsi dans l’ananas. forment des spirales qui comportent un nombre précis de ces même écailles Un Ananas… 5 écailles… 8 écailles… Et 13 écailles 5,8,13.. encore des termes successifs de la suite de Fibonacci. Le chou-fleur. De même, on trouve des spirales dans le chou-fleur : en observant ce légume, on peut voir que l’on peut former une spirale en rejoignant les petits espaces formés entre deux petits morceaux.. Un chou-fleur et ses spirales tracées en bleu et en rouge. Dans le schéma ci-dessus, on voit bien qu’on peut faire ressortir deux types de spirale : · celles orientées dans le sens direct (rouge) : 5 spirales · celles orientées dans le sens indirect (bleu) : 8 spirales 5…8… encore deux termes qui nous amènent vers j. La pomme de pin. 4).
Le nombre d'or L' histoire ... Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos . Il utilise également la racine carrée de 5 comme rapport. IIIè siècle avant J-C. : Euclide évoque le partage d'un segment en "extrême et moyenne raison" dans le livre VI des Eléments. 1498 : Fra Luca Pacioli, un moine professeur de mathématiques, écrit De divina proportione ("La divine proportion"). Au cours du XXème siècle : des peintres tels Dali et Picasso, ainsi que des architectes comme Le Corbusier, eurent recours au nombre d'or.
nombre d’or Définition, traduction, prononciation, anagramme et synonyme sur le dictionnaire libre Wiktionnaire. Français[modifier] Étymologie[modifier] (Mathématiques) Calque de l’allemand goldener Schnitt, lui-même utilisé par Martin Ohm en 1835. (Astronomie) Calque du latin numerus aureus. Locution nominale [modifier] nombre d’or \nɔ̃.bʁə d‿ɔʁ\ masculin singulier (Mathématiques) Nombre irrationnel qui définit des proportions agréables aux sens humains, fondé sur le fait que le rapport d’une partie à une autre soit identique au rapport de cette dernière au tout. Apparentés étymologiques[modifier] → voir nombre et or Vocabulaire apparenté par le sens[modifier] Traductions[modifier] Voir aussi[modifier] Nombre d’or sur Wikipédia
Nombre d'or Un article de Wikipédia, l'encyclopédie libre. La proportion définie par et est dite d'« extrême et moyenne raison » lorsque est à ce que , soit : lorsque . est alors égal au nombre d'or. Le nombre d'or est une proportion, définie initialement en géométrie comme l'unique rapport entre deux longueurs telles que le rapport de la somme des deux longueurs ( ) sur la plus grande ( ) soit égal à celui de la plus grande ( ) sur la plus petite ( ) c'est-à-dire lorsque . Ce nombre irrationnel est l'unique solution positive de l'équation . soit approximativement[1] 1,6180339887. Il est érigé en théorie esthétique et justifié par des arguments d'ordre mystique, comme une clé importante, voire explicative, dans la compréhension des structures du monde physique, particulièrement pour les critères de beauté et surtout d'harmonie ; sa présence est alors revendiquée dans les sciences de la nature et de la vie, proportions du corps humain ou dans les arts comme la peinture, l'architecture ou la musique. , où
Nombre d'or et art : mythe ou réalité ? Juin 2006 Depuis l'Antiquité, artistes et philosophes croient à l'existence d'une proportion privilégiée permettant d'obtenir harmonie et beauté. C'est à Euclide que l'on doit les premières traces écrites du fameux nombre d'or. Pourquoi nombre d'or ? L'esthétique du rectangle d'or Pour en avoir le cur net, Fechner un philosophe allemand (1801-1887) soumet à quelques centaines de personnes plusieurs rectangles, chaque personne devant designer le rectangle le plus "attrayant". Seulement plusieurs points viennent mettre en doute ces résultats. Vers 1930, le Roumain Matila Ghyka voit du nombre d'or partout, dans la nature comme dans l'architecture et la peinture. Mais ses mesures sont contestables, approximatives. Par la suite, de nombreux scientifiques ont essayé de valider ou non, cette théorie du nombre d'or. De son côté, George Markowsky propose un test avec 48 rectangles de proportions différentes (entre 0.4 et 2.5), à hauteur fixe, et à largeur variable. Les secrets du "beau"
Redresser l’horizon C’est l’un des premiers trucs qu’on vous dira sur tous les forums photos : « c’est pas droit », et c’est aussi quelque chose qui se corrige facilement et fait toute la différence. De quoi parle-t-on exactement ? De cette impression de penché. On visualise la ligne d’horizon, et celle-ci, même si la terre est ronde, se doit de rester droite (nous évoquerons les exceptions dans quelques lignes). C’est particulièrement visible sur les paysages avec de l’eau. Si vous penchez un verre, le niveau de l’eau reste parallèle à la table. Si vous êtes normalement constitués, vous devriez préférer la deuxième version. En faisant attention à la prise de vue, c’est facile de faire une photo droite, et pas besoin d’acheter les niveaux à bulles qu’on peut essayer de vous vendre dans certains magasins. Il arrive parfois qu’on bouge un peu, ou que l’on se plante, tout simplement. Cette règle sera utile dans beaucoup de situations. Il y a des cas plus compliqués : les déformations.
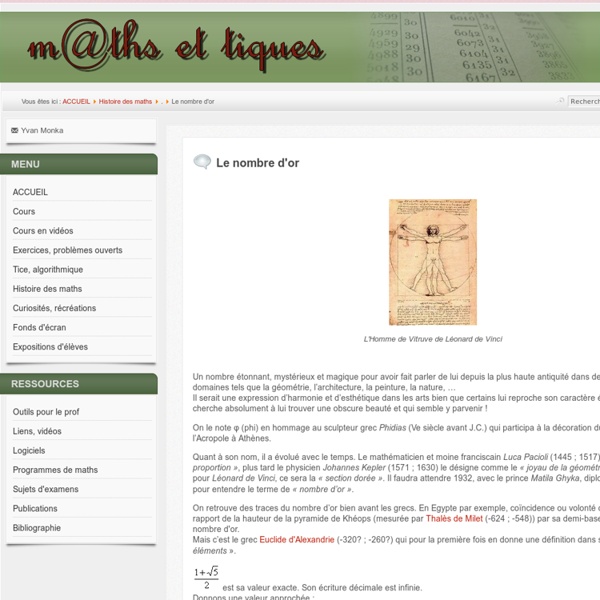
Le nombre d'or L'Homme de Vitruve de Léonard de Vinci Un nombre étonnant, mystérieux et magique pour avoir fait parler de lui depuis la plus haute antiquité dans de nombreux domaines tels que la géométrie, l’architecture, la peinture, la nature, … Il serait une expression d’harmonie et d’esthétique dans les arts bien que certains lui reproche son caractère ésotérique qui cherche absolument à lui trouver une obscure beauté et qui semble y parvenir ! On le note φ (phi) en hommage au sculpteur grec Phidias (Ve siècle avant J.C.) qui participa à la décoration du Parthénon sur l’Acropole à Athènes. Quant à son nom, il a évolué avec le temps. Le mathématicien et moine franciscain Luca Pacioli (1445 ; 1517) parle de « Divine proportion », plus tard le physicien Johannes Kepler (1571 ; 1630) le désigne comme le « joyau de la géométrie ». On retrouve des traces du nombre d’or bien avant les grecs. est sa valeur exacte. Le rectangle d'or .Lien externe vers une animation. La spirale d'or Le triangle d'or En algèbre
règle tiers Comment composer une photographie ? Il n’y a heureusement pas de réponse définie à cette question, laissant aux photographes une grande liberté de création. Mais un certain nombre de règles de composition sont établies et facilitent la création d’images. Nous allons voir dans cet article quelques éléments basiques de composition. 1. La règle d’or La règle d’or a été définie par un architecte romain, Marcus Vitruvius Pollio. Voici un rectangle ayant les dimensions préconisées par la règle d’or. Les lignes de forces En définissant des points à chaque intersection des rectangles dans l’image ci-dessus, on définit des lignes de forces horizontales, verticales et obliques. Si l’on entrecoupe ces lignes, on définit alors d’autres lignes de forces Les points forts Si l’on applique la règle d’or à la photographie, on peut déterminer plusieurs lignes de forces. Le schéma ci-dessous montre toutes les lignes de forces ainsi que les points forts primaires (en rouge) et secondaires (en bleu). A bientôt,
Nombre d'or - ce qu'il faut savoir en bref Étapes de construction 1) Je construis un carré ABCD de 10 carreaux de côté. 2) Je positionne le point milieu M, en bas. 3) Je dessine un cercle de centre M et de rayon MB; il coupe la droite DC en F. 4) Le rectangle ABEF est un rectangle d'or. Mesures et conclusions Je mesure le grand côté DF: 16,2 carreaux Le rapport (ou le quotient) entre les mesures de la longueur et de la largueur est Si je calcule le rapport pour le rectangle BEFC, je trouve Soit, à peu près la même valeur. Ce nouveau rectangle BEFC est aussi un rectangle d'or. Valeur exacte du nombre d'or Le triangle BCM est rectangle, je peux lui appliquer le théorème de Pythagore: Cette valeur confirme les mesures effectuées sur les deux rectangles. La règle des tiers : Premier outil des pros pour composer | Cours de Photo La Règle des Tiers : Un fondement de la composition Dans les cours de photo, la règle des tiers est LA règle de base d’aide à la composition. Elle est simple, pratique et facile à apprendre. Appliquez-la dès maintenant pour des résultats immédiats! Le réflexe naturel de ceux qui débutent est de placer systématiquement le sujet au centre de l’image. Pour appliquer la règle des tiers, on divise « virtuellement » l’image cadrée en 9 zones égales à l’aide de deux lignes horizontales et deux lignes verticales, comme ceci en mode « paysage » : On obtient quatre lignes dénommées : Tiers SupérieurTiers InférieurTiers GaucheTiers Droit Les intersections deviennent alors : Le Tiers Supérieur Gauche – Le Tiers Supérieur DroitLe Tiers Inférieur Gauche – Le Tiers Inférieur Droit Certains appareils photographiques proposent d’afficher une grille de ce type dans le viseur ou sur l’écran de visualisation. En mode « portrait », cela donne ceci : Exemples d’utilisation de la règle des tiers Et VOUS ?
Dossier - La suite de Fibonacci et le nombre d'or - Podcast Science Disclaimer : Ouh-la, cet article du tout début de notre site est un peu étrange ! On s’était apparement laissé un peu avoir par la nombre-d’or-mania et, avec quelques années de recul, on est pas extrêmement fier de son contenu. L’équipe de Podcast Science Dossier de Mathieu dans l’épisode #28. La suite de Fibonacci doit son nom au mathématicien italien Leonardo Fibonacci qui a vécut au XIIème et XIIIème siècle. Mais il est aussi connu pour avoir mis en évidence une suite mathématique qui porte désormais son nom. Il suffit de prendre deux nombres de départ. La suite de Fibonacci possède de nombreuses propriétés très utilisées en mathématiques. En effet: 13/8 = 1.625 ; 21/13 = 1.61538… ; 34/21 = 1.61904…et ainsi de suite…plus on avance dans la suite de Fibonacci, plus l’écart s’amenuise, et plus le rapport des deux nombres successifs (le plus grand / le plus petit) tend vers la valeur du nombre d’or 1,61803…! Sources:
Le nombre d’or, la règle des tiers dopée Bienvenue sur Apprendre la Photo !Si vous êtes nouveau ici, vous voudrez sans doute lire mon guide qui répond aux 5 problèmes courants des débutants : Cliquez ici pour télécharger le guide gratuitement !Merci de votre visite, et à bientôt sur Apprendre la Photo ! :) Si vous avez un peu exploré le blog et vous êtes intéressé à la composition de vos photos, vous avez forcément entendu parler de la règle des tiers. En général, quand on découvre la règle des tiers en débutant la photographie, ça révolutionne un peu notre vision du monde, des images et on finit par découvrir qu’on a passé sa vie à centrer le sujet, et que c’est ce qui donnait des images moches pas top. Et bien aujourd’hui, je vais vous parler d’une règle de composition qui y ressemble un peu, mais qui a encore plus de force. Ah non, tu déconnes ? Pas d’inquiétude, je ne ferai pas dans le compliqué Spirale de phi Ça ressemble à la règle des tiers, ça a l’odeur de la règle des tiers… mais ce n’est pas la règle des tiers !
suite de Fibonacci dans la nature Loi Les bourgeons tenteraient de disposer du maximum de lumière et de place. Le premier se place. Le second se positionne à un peu plus de 120°, en fait: Et les suivants tentent de conserver cet espacement de 137,5°. Voir Méristème apical Tableau Illustration Voilà, le sixième qui se trouve un peu à l'ombre du premier pétale. Moins de 50° pour se loger (32,5°). Est-ce la bonne raison ? C'est en tout cas ce que l'on peut lire dans quelques ouvrages sur le sujet. De nombreuses simulations sont faites pour retrouver à partir de telles hypothèses les dispositions en spirale des tournesols, des feuilles sur les tiges, des dessins du chou-fleur … Vocabulaire Foliation ou Phyllotaxie: disposition des feuilles sur la tige. Phyllotaxis: anglais pour foliation, leaf arrangement.