

Éval 112 sujet 1. Corrigé éval 112 sujet 1. Éval 112 sujet 2. CORRIGE 112 sujet 2. Éval 102 sujet 1. Corrigé 102 sujet 1. Éval 102 sujet 2. Corrigé 102 sujet 2. Algo fibonacci. Calculatrice en papier. Calculatrice graphique. Révision Cours calcul littéral. Nouveau Cours fonction polynôme de degré 2. 96p23 et 166 p 29. Programme python 153 p 28. 154 p 28 nouveau manuel. Algo discriminant et somme des inverses des carres pi26. Algo sommet parabole. Le nombre d'or. (Vitruve, architecte romain 1er siècle avant notre ère). Ainsi si a et b sont les deux grandeurs alors nous aurons : a/b = (a + b) / a. A/b = 1 + b/a pour simplifier, prenons comme variable x = a/b. alors nous obtenons : x = 1 + 1/x x - 1 - 1/x = 0 comme x non nul, nous obtenons l'équation suivante que nous noterons (E) : x2 - x - 1 = 0 qui admet comme racine positive : x = que nous notons Φ et vaut à peu près 1,618... C'est cette valeur qui est appelée le nombre d'or (dit Φ (phi) en hommage au sculpteur grec Phidias qui s'en servit dans les proportions du Parthénon à Athènes.
En espagne, deux tableaux de Antonio de Garcia de Pablo, muchas gracias ;): Pour voir les images suivantes en plus grand les cliquer A ce stade, je vous soumets un petit problème que m'a proposé Dominique Payeur : Je dispose d'un capital. Le nombre d'or. Fruits d'Eucalyptus provenant de Galice en Espagne.

On trouve des pentagones réguliers, mais aussi des carrés er des triangles équilatéraux. Lien avec l'ensoleillement Cela vient de ce que l'ensoleillement doit être maximum pour toutes les feuilles et on démontre que l'angle de deux feuilles consécutives doit être voisin d'un certain k ème de tour ; les fractions de Fibonacci sont les fractions les plus voisines de k. Les graines dans une fleur de tournesol Ammonite L'enroulement régulier d'une ammonite se fait suivant une spirale logarithmique. La découverte des quasicristaux, de molécules en forme de dodécaèdre (constitué de 12 pentagones), de certains virus ayant cette forme montre que la symétrie d'ordre cinq est assez fréquente dans la nature.
" On doit être chez Fibonacci ! Voir aussi les liens externes suivants : géométrie dans la nature et aussi une vidéo splendide La nature par les nombres. Polynômes et équations du second degré. Trouver l'erreur (Can You Spot the Mistake?) Conique. CONIQUEConic section, Kegelschnitt La définition actuelle d’une conique est d’être une courbe algébrique du deuxième degré.Cette définition englobe les cas de dégénérescence (dans le plan euclidien : ensemble vide, point, réunion de deux droites) et permet d’affirmer que les coniques sont les sections planes des quadriques.Cependant, dans ce site, le mot conique désigne uniquement les cas non dégénérés, ou "propres" : ellipse, parabole, hyperbole.

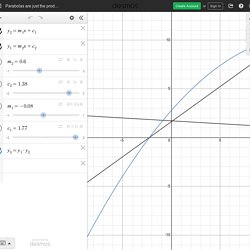
Avec cette acception, voici diverses définitions géométriques des coniques : 1) Définition des Grecs.Les coniques sont les sections d’un cône de révolution par un plan ne passant pas par son sommet. 2) Définition par foyer et directrice. Les coniques sont des cercles, ou les lieux des points dont le rapport des distances à un point fixe (le foyer F) et à une droite fixe (la directrice (D)) est constant (égal à l’excentricité e) ; les ellipses sont obtenues pour e < 1, la parabole pour e = 1, les hyperboles pour e > 1. Parabolas are just the product of straight lines. Parabolas are just the product of straight lines Create AccountorSign In «1x» «2x» «0.35x» «0.5x» powered by powered by functions $$π Create AccountorSign In.
Les coniques à la plage - Micmaths. LE PLUS FOU DES OBJETS ! (four solaire PARABOLIQUE) Pourquoi les pommes tombent et pas la lune. YouTube. Multiplying monkeys and parabolic primes. Le vol parabolique : mode d'emploi. Les lois de Kepler. M Johannes Kepler (1571-1630) Astronome allemand.

À partir de 1600, il exploite les données recueillies par Tycho Brahé. Découvre en tout premier lieu la deuxième loi sur l'aire balayée. Étudie l'orbite exacte de Mars. Il doit admettre que l'orbite n'est pas circulaire, mais elliptique (1606). Publie à 23 ans: Le Secret du monde. Favorable à l'hypothèse héliocentrique de Copernic: la Terre tourne autour du Soleil. En 1618, termine son œuvre avec L'Harmonie du monde en y introduisant sa troisième loi. En optique, propose la dioptrie. Sa célèbre conjecture sur l'empilement des sphères. Les lois de Kepler. Intégrer ce média sur votre site.
Parabole. La parabole est une courbe plane, symétrique par rapport à un axe, approximativement en forme de U.
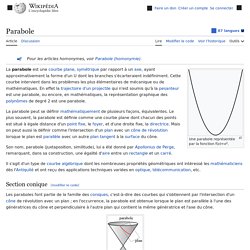
Il s'agit d'un type de courbe algébrique dont les nombreuses propriétés géométriques ont intéressé les mathématiciens dès l'Antiquité et ont reçu des applications techniques variées en optique, télécommunication, etc. Mathématiques[modifier | modifier le code] Section conique[modifier | modifier le code] La parabole est l'intersection d'un plan avec un cône de révolution lorsque le plan est parallèle à une des génératrices du cône.
Directrice, foyer et excentricité[modifier | modifier le code] Parabole de droite directrice d et de foyer F. Début d'année.