

Tableur et Python: échantillonnage, vérification des "95%" Python: pi avec Monte Carlo. Le paradoxe de Simpson — Science étonnante #7. Réformons l'élection présidentielle ! — Science étonnante #35. Monsieur le président, avez-vous vraiment gagné cette élection ? Tous racistes ? Les biais implicites — Crétin de Cerveau #7. Pourquoi gagnez-vous moins que le salaire moyen ? Chocolat, corrélation et moustache de chat.
Chapitre 5 Fluctuation d'échantillonnage. Thème : Probabilités.
Test d'entrée Thème : Probabilités Fiche d'exposé 1)Plan de la séquence I. Test d'entrée Avant d entamer le travail sur les probabilités, il semble pertinent de proposer aux élèves un test d'entrée pour établir un état Plus en détail Loi normale et échantillonnage Loi normale et échantillonnage 1. Plus en détail LES PROBABILITÉS. Ch 9 LES PROBABILITÉS Sommaire 0- Objectifs 1- Expérience aléatoire 2- Modèles et probabilités 3- Expérience aléatoire à deux épreuves 4- Simulation d'une expérience aléatoire 0- Objectifs Comprendre et Plus en détail Échantillonnage - Estimation Échantillonnage - Estimation 2 nde Introduction : Ce chapitre répond à deux types de questions : Exemple d'introduction. Plus en détail Exercices sur les probabilités Exercices sur les probabilités Exercice N 1 : Mots croisés. Plus en détail Expérimenter, d abord à l aide de pièces, de dés ou d urnes, puis à l aide d une simulation informatique prête à l emploi, la prise d échantillons Plus en détail T ES/L.
Fluct echantillonnage. Fluctuation. 2nde fluctuation. Cours 9. Fluctuation d'une fréquence selon les échantillons, probabilités - Maths-Sciences XT. Taille de l’échantillon de sondage – Évaluez le nombre de personnes à interroger. Intervalle de confiance : Cours - comment ... Intervalle de FLUCTUATION V.S. Intervalle de CONFIANCE. 15 EchantillonnageM.
"Maths; Cours de terminale ES "; Intervalles de fluctuation, de confiance. Définition On obtient un échantillon de taille si l'on répète fois une expérience à 2 issues (souvent appelées "succès" et "échec") et si les expériences sont indépendantes.

Exemple 1 On jette 100 fois de suite un dé et l'on compte le nombre de 6 obtenus. On a là un échantillon de taille 100. Notons que les 2 issues sont: "obtenir 6", et "ne pas obtenir 6". Exemple 2 On interroge 100 électeurs parmi 10000, et on leur demande à chaque fois s'ils vont voter pour le candidat Machin. On considère un échantillon de taille , associé à la probabilité de succès (ou à la proportion du caractère étudié ). Statistiques intervalle de confiance. Imaginons un maitre qui connait tout, et un élève qui, lui, doit estimer.

Notre population (population mère ou population réelle) comprend des milliers d'individus dont le maitre sait que la moyenne de leur taille est 180 cm (µ = 180). L'élève doit tenter de retrouver cette moyenne en se fiant à un petit nombre de personnes interrogées (échantillon). Collecte des infos puis calculs faits, il trouve 181 cm. Sauter le pas et dire que c'est la bonne valeur (inférence) serait fallacieux, n'est-ce pas? Intervalle de confiance. Un intervalle de confiance doit être associé à un niveau, en général sous la forme d’un pourcentage, qui minore la probabilité de contenir la valeur à estimer.
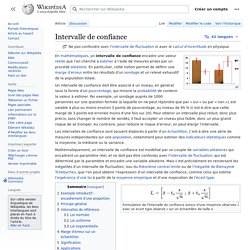
Par exemple, un sondage auprès de 1000 personnes sur une question fermée (où l’on ne peut répondre que par « oui » ou par « non »), est valable à plus ou moins 3 points de pourcentage, au niveau de 95 % (c’est-à-dire que cette marge n’est pas valable moins d’une fois sur 20). Pour obtenir un intervalle plus réduit, donc plus précis, sans changer le nombres de sondés, il faut accepter un niveau plus faible, donc un plus grand risque de se tromper. Au contraire, pour réduire le risque d’erreur, on peut élargir l’intervalle. Mathématiquement, un intervalle de confiance est modélisé par un couple de variables aléatoires qui encadrent un paramètre réel, et ne doit pas être confondu avec l'intervalle de fluctuation, qui est déterminé par le paramètre et encadre une variable aléatoire. Si on cherche à évaluer quelle proportion . Et. . , où. Taille d'un échantillon aléatoire et Marge d'erreur.
Introduction Lorsque l’on effectue une enquête on s’intéresse à une population mère (population totale) dont on va généralement interroger une petite partie, c’est l’échantillon dont il faut déterminer la taille soigneusement car elle a une grande importance sur la précision des estimations réalisées sur les caractéristiques de la population-mère.
Pour des raisons économiques, il est nécessaire d’utiliser une taille d’échantillon la plus réduite possible tout en obtenant un taux de confiance et une marge d’erreur suffisants. Paramètres en jeux Dans ce qui suit on appelle : On définit également : Le Taux de sondage R = n/N La Fourchette d’incertitude I = 2e. La théorie statistique fourni les équations qui expriment les relations entre ces paramètres. Les Taux de confiance « s » les plus utilisés et les Coefficients de marge « t » associés sont donnés dans le tableau suivant :
Fluctuconf2. AAA03013. Ts echantillonnage estimation.