

Théorème de Jordan. Un article de Wikipédia, l'encyclopédie libre.
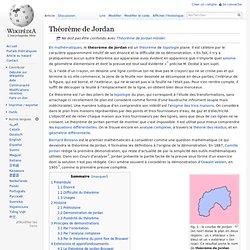
En mathématiques, le théorème de Jordan est un théorème de topologie plane. Il est célèbre par le caractère apparemment intuitif de son énoncé et la difficulté de sa démonstration. « En fait, il n'y a pratiquement aucun autre théorème qui apparaisse aussi évident en apparence que n'importe quel axiome de géométrie élémentaire et dont la preuve est tout sauf évidente »[1] précise M. Dostal à son sujet. Si, à l'aide d'un crayon, on dessine une ligne continue (on ne lève pas le crayon) qui ne se croise pas et qui termine là où elle commence, la zone de la feuille non dessinée se décompose en deux parties, l'intérieur de la figure, qui est borné, et l'extérieur, qui ne le serait pas si la feuille ne l'était pas.
Pour s'en rendre compte, il suffit de découper la feuille à l'emplacement de la ligne, on obtient bien deux morceaux. Courbe de Jordan. Julie Distexhe- Autour du théorème de Jordan. Courbe. COURBECurve, Kurve C'est une très bonne question et je ne vous remercie pas de me l'avoir posée !
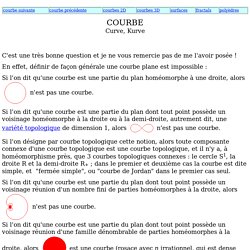
En effet, définir de façon générale une courbe plane est impossible : Si l'on dit qu'une courbe est une partie du plan homéomorphe à une droite, alors n'est pas une courbe. Si l'on dit qu'une courbe est une partie du plan dont tout point possède un voisinage homéomorphe à la droite ou à la demi-droite, autrement dit, une variété topologique de dimension 1, alors Si l'on désigne par courbe topologique cette notion, alors toute composante connexe d'une courbe topologique est une courbe topologique, et il n'y a, à homéomorphisme près, que 3 courbes topologiques connexes : le cercle S1, la droite R et la demi-droite R+ ; dans le premier et deuxième cas la courbe est dite simple, et "fermée simple", ou "courbe de Jordan" dans le premier cas seul.
Ter_2011.pdf. Le théorème de Jordan. Prenez une feuille de papier, et un stylo.
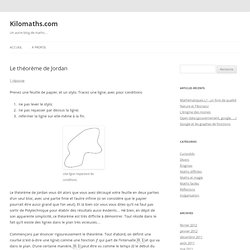
Tracez une ligne, avec pour conditions ne pas lever le stylo;ne pas repasser par dessus la ligne;refermer la ligne sur elle-même à la fin. Une ligne respectant les conditions. Le théorème de Jordan vous dit alors que vous avez découpé votre feuille en deux parties d’un seul bloc, avec une partie finie et l’autre infinie (si on considère que le papier pourrait être aussi grand que l’on veut). Et là bien sûr vous vous dites qu’il ne faut pas sortir de Polytechnique pour établir des résultats aussi évidents… Hé bien, en dépit de son apparente simplicité, ce théorème est très difficile à démontrer.
Commençons par énoncer rigoureusement le théorème. Qui part de l’intervalle et qui va dans le plan. Peut être vu comme le temps (0 le début du tracé, 1 la fin) et le point tracé exactement à l’instant . . À deux instants. Sphère cornue d'Alexander. Un article de Wikipédia, l'encyclopédie libre.
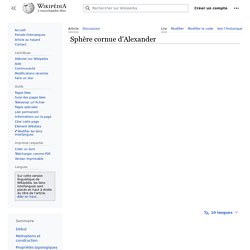
Sphère cornue d'Alexander En mathématiques, et plus précisément en topologie, la sphère cornue d'Alexander est un célèbre exemple de surface pathologique ; elle fut découverte en 1923 par J. W. Alexander. Motivations et construction[modifier | modifier le code] Il semble évident qu'une courbe fermée simple (ne se recoupant pas) du plan le découpe en deux régions (l'intérieur et l'extérieur) et qu'on peut déformer la courbe (et les deux régions séparées) pour la transformer en un cercle. L'idée intuitive de la construction d'Alexander est de rajouter à la sphère usuelle des « cornes » se ramifiant et s'entrelaçant indéfiniment. En ne considérant que les points ajoutés à l'étape 2 et qui ne sont jamais retirés lors des étapes 1 ultérieures, on obtient un plongement de la sphère à laquelle a été retiré un ensemble de Cantor.
Propriétés topologiques[modifier | modifier le code] Notes et références[modifier | modifier le code] ↑ (en) J. La sphère cornue. La sphère à cornes, sculpture de Jean-Louis Lhermitte, dans la cour du Centre de mathématiques et d’informatique Prenez un crayon, une feuille de papier et dessinez-y une courbe revenant à son point de départ sans lever le crayon, ni passer deux fois sur le même point : Vous obtenez quelque chose comme ça.

LA SPHÈRE CORNUE D’ALEXANDER, PAR JOS LEYS. L'image du jour Une courbe fermée qui ne se recoupe pas décompose le plan en deux composantes : c’est le théorème de Jordan.
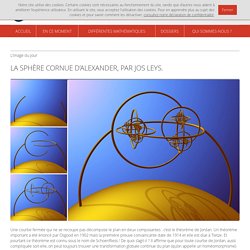
Un théorème important a été énoncé par Osgood en 1902 mais la première preuve convaincante date de 1914 et elle est due à Tietze. Et pourtant ce théorème est connu sous le nom de Schoenfliess ! De quoi s’agit-il ? Il affirme que pour toute courbe de Jordan, aussi compliquée soit-elle, on peut toujours trouver une transformation globale continue du plan (qu’on appelle un homéomorphisme) qui applique la courbe sur un cercle.