

Les trois géométries. Mathématicien russe, recteur de l'université de Kazan.

Géométrie imaginaire publié en russe en 1829, puis en français en 1837. Elle dit que par un point extérieur à une droite passent deux droites parallèles à cette droite. Argument de Lobatchevsky Soit deux droites D1 et D2. La perpendiculaire D à D2 coupe D2. Géométrie non euclidienne. En mathématiques , la géométrie non euclidienne se compose de deux géométries basées sur des axiomes étroitement liés à ceux qui spécifient la géométrie euclidienne .

Comme la géométrie euclidienne se situe à l'intersection de la géométrie métrique et de la géométrie affine, la géométrie non euclidienne survient soit en relâchant l'exigence métrique, soit en remplaçant le postulat parallèle par une alternative. Dans ce dernier cas on obtient la géométrie hyperbolique et la géométrie elliptique , les géométries non euclidiennes traditionnelles. Lorsque l'exigence métrique est assouplie, il y a des plans affines associés aux algèbres planaires, qui donnent lieu à des géométries cinématiques qui ont également été appelées géométrie non euclidienne.
Comportement des lignes avec une perpendiculaire commune dans chacun des trois types de géométrie Histoire. 111 - A 3D model collection by Evgeniy.Polozov (@Evgeniy.Polozov) Henry Segerman (@henryseg) Barbara Schapira - Triangles et géométries. What Is The Shape of Space? (ft. PhD Comics) Géométries euclidienne et non euclidiennes. Non euclidian geometries. VISUALISER LA COURBURE. Comprendre la notion de courbure sans aucune formule...

Du simple rayon de courbure jusqu’au tenseur de Riemann, clé de voûte de la géométrie différentielle. Baptiste Chantraine - Le théorème de Girard pour les triangles sphériques. La formule de Girard. Vous avez manqué la dernière vidéo qui parle de géométrie sphérique ?
Il n’est jamais trop tard pour aller la regarder ! Dans cette vidéo, je mentionne une propriété très importante en géométrie sphérique : la somme des angles d’un triangle y est toujours supérieure à 180 degrés (ou plutôt π radians, puisque nous utiliserons plutôt cette unité d’angle pour la suite). Courbure de Gauss. De gauche à droite : une surface de courbure de Gauss négative (un hyperboloïde), une surface de courbure nulle (un cylindre), et une surface de courbure positive (une sphère).
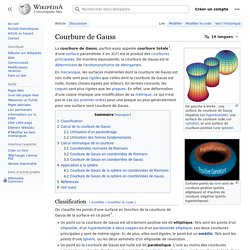
Certains points du tore sont de courbure positive (points elliptiques) et d'autres de courbure négative (points hyperboliques) Classification[modifier | modifier le code] On classifie les points d'une surface en fonction de la courbure de Gauss de la surface en ce point[1]. Calcul de la courbure de Gauss[modifier | modifier le code] Cercle osculateur et courbure. Les angles d'un triangle s'additionnent-ils jusqu'à 180° ? - Présentation de la géométrie non-euclidienne (anglais) Hyperbolic Football. We explain what is the meaning of the angle sum (and also what is the acute angle in our Lambert quadrilateral above).

If you have really careful participants, this can be a fascinating discovery activity. We remarked that the model is mostly flat. In fact, its curvature is concentrated at the vertices, where two hexagons and one heptagon meet. The sum of the angles at that vertex is. Théorème de Gauss-Bonnet diaporama CM S5. Axiomatique d'Euclide, convexité, géométries non euclidiennes (Daniel Perrin) Des fondements de la geometrie. (The Monist, 1898).

DES FONDEMENTS DE LA GÉOMÉTRIE Quoique j'aie déjà eu l'occasion d'exposer mes idées sur les fondements de la géométrie, il ne sera peut-être pas sans intérêt de revenir sur cette question avec de nouveaux développements et de chercher à éclaircir certains points que le lecteur peut avoir trouvés obscurs. C'est au sujet de la définition du point et de la détermination du nombre des dimensions que de nouveaux éclaircissements me paraissent le plus nécessaires ; mais cependant je crois utile de reprendre la question par le commencement. L'ESPACE SENSIBLE Nos sensations ne peuvent pas nous donner la notion d'espace. Cette notion est construite par l'esprit avec des éléments qui préexistent en lui, et l'expérience externe n'est pour lui que l'occasion d'exercer ce pouvoir, ou au plus un moyen de déterminer la meilleure manière de l'exercer.
Les sensations par elles-mêmes n'ont aucun caractère spatial. DPPartie4. Géométrie non euclidienne. In about 300 BC Euclid wrote The Elements, a book which was to become one of the most famous books ever written.

Euclid stated five postulates on which he based all his theorems: To draw a straight line from any point to any other. To produce a finite straight line continuously in a straight line. To describe a circle with any centre and distance. That all right angles are equal to each other. That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
Géométries euclidienne et non euclidiennes. Les trois premiers postulats sont les règles du jeu de la construction à la règle et au compas.
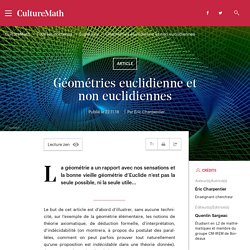
Dans le premier postulat, l’unicité de la ligne droite joignant les deux points quelconques n’est pas spécifiée ; dès qu’Euclide a besoin de cette unicité (dans la preuve de la proposition 4) il la « justifie » en prétendant que si deux lignes droites joignaient deux mêmes points elles délimiteraient une aire ; or, l’une des « notions communes » (axiomes) dit que deux lignes droites ne délimitent pas une aire. L’argument serait convaincant s’il était formellement prouvé qu’en effet deux lignes droites qui joindraient deux mêmes points devraient délimiter une aire : mais cette affirmation semble reposer sur une intuition géométrique et non sur des règles claires… Il serait plus simple d’énoncer d’emblée l’unicité dans le premier postulat.
Ce à quoi Euclide (ou l’un de ses successeurs) ajoute : Deux lignes droites ne délimitent pas une aire. Géométries non euclidiennes. DES GRAPHES À COURBURE POSITIVE. Dans son billet, Christian Bonatti écrivait qu’il y a sûrement des sujets mathématiques assez difficile à vulgariser, prenant comme exemple le thème du séminaire auquel il avait assisté la veille.
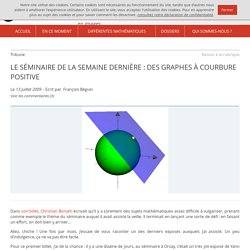
Il terminait en lançant une sorte de défi : en faisant un effort, on doit bien y arriver... Allez, chiche ! Une fois par mois, j’essaie de vous raconter un des derniers exposés auxquels j’ai assisté. Un peu d’indulgence, ça ne va pas être facile. Géométries non euclidiennes. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Considérons un segment [AB]. Élevons les segments isométriques [BC] et [AD] perpendiculaires à [AB]. Joignons C et D. On obtient un quadrilatère de Saccheri, du nom d'un philosophe et mathématicien italien du qui s'intéressa au bien fondé de l'axiomatique euclidienne : 436 - Des Mathémachips. Demi-plan de Poincaré. Transformation de Möbius. En mathématiques, et plus particulièrement en géométrie, les transformations de Möbius sont de manière générale des automorphismes du compactifié d'Alexandrov de noté , définies comme la composée d'un nombre fini d'inversions par rapport à des hyperplans ou des hypersphères.
En particulier, si on identifie à la sphère de Riemann , alors on peut prouver que les transformations de Möbius conservant l'orientation sont de la forme : avec a, b, c et d quatre complexes tels que ad – bc ≠ 0, la formule ci-dessus étant à prendre au sens suivant si z = ∞ ou si cz + d = 0 : Définition générale[modifier | modifier le code] Soit n un entier naturel, on munit ℝn de sa structure euclidienne canonique et on définit alors les inversions de. Action par conjugaison. Un article de Wikipédia, l'encyclopédie libre. Définitions[modifier | modifier le code] Notons ici, pour tout élément g de G, l'automorphisme intérieur de G associé à g (c'est un automorphisme de G).
Alors, l'application g ↦ autg, de G dans SG, est un morphisme de groupes. En effet, autg∘auth = autgh.
Trigonométrie sphérique. Triangle sphérique[modifier | modifier le code] La somme des angles d'un triangle sphérique peut varier entre 180 et 540° (entre π et 3π radians)[a],[1]. Formules fondamentales[modifier | modifier le code] Triangle sphérique avec ses grands cercles et ses angles au centre (l’angle a s’identifie à BC si on suppose le rayon égal à 1) Conventions[modifier | modifier le code] On considère trois points A, B et C sur une sphère comme représentés par la figure ci-contre, ainsi que les arcs de grands cercles qui les relient. ) l'angle du triangle au sommet A, et de façon analogue pour les autres sommets. . , etc. LE THÉORÈME DE GIRARD POUR LES TRIANGLES SPHÉRIQUES. Un épisode de la série les 5 minutes Lebesgue Le 29 octobre 2017 - Ecrit par Collectif Les 5 minutes Lebesgue S’abonner aux 5 minutes Lebesgue : Les 5 minutes Lebesgue sont une série vidéo proposée par le Centre Henri Lebesgue. Elle consiste en des exposés mathématiques, indépendants les uns des autres, qui durent chacun cinq minutes chrono !
Les sujets sont variés et s’adressent à différents publics allant du grand public au mathématicien spécialisé. Comment jouer aux billes dans un espace courbe ? - Schapira - Une question, un chercheur - 04/04/19. Bourguignon Jean-Pierre - "Espaces courbes de Gauss à Perelman, en passant par Einstein" - 2010. Villarceau analyse cercles sur le tore. Cédric Villani - 1/7 La théorie synthétique de la courbure de Ricci. Surface de Boy. Animation de la surface de Boy. dans l'espace usuel de dimension 3. Le plan projectif se définit comme l'espace quotient de par la relation d'équivalence qu'est la colinéarité. La surface de Boy peut aussi être « vue » comme une sphère dont on a recollé deux à deux les points antipodaux, ou encore un disque dont on a recollé deux à deux les points diamétralement opposés de son bord.
Vue de la surface de Boy dans un espace à trois dimensions. CSG Boy's surface. Math related computer generated images. Modular hyperbolic tilings Modular hyperbolic tilings, black and white Klein's quartic. Vincent Colin - Comment mesurer la forme d'un espace ? RG7 - La géométrie courbe. Enlacement dans les fibrés en tores et fonctions L de Hecke - WebTV Université de Lille.
How to embed a flat torus in 3D Euclidean space. John Nash Peut-on coller les côtés opposés d'une feuille carrée ? Relativité 9. Comment Mikhaïl Gromov inventa la machine à démanteler les impossibles. Nous poursuivons avec cet article la suite de notre série sur le cycle « Un texte, un mathématicien ». Aujourd’hui, Vincent Borrelli évoque l’œuvre de Mikhaïl Gromov, mathématicien russe qui travaille aujourd’hui en France.
Il y a trente ans exactement paraissait un ouvrage mathématique austère. Son titre « Relations aux dérivées partielles » sonnait étrangement, même aux oreilles des spécialistes, sa couverture était minimaliste, son écriture serrée, son contenu abstrait. Chacune de ses 363 pages réclamait une concentration complète et n’offrait aucune facilité de lecture. Il n’était pas difficile de deviner les réactions qu’il allait susciter : un intérêt poli suivi d’un oubli immédiat. Mais c’était sans compter l’immense réputation de son auteur, l’un des plus grands mathématiciens contemporains, Mikhaïl Gromov. Plat comme un tore. Un tore carré et plat.
GNASH, UN TORE PLAT ! Projet Hévéa. Flying over a 3D fractal flat torus. GÉOMÉTRIE ET DYNAMIQUE DES SURFACES PLATES. Surfaces plates Le sujet de cet article est l’étude de la géométrie des surfaces lorsqu’elles sont munies d’une métrique plate. Non-Euclidean Worlds Engine. Essai d'interprétation des géométries non euclidiennes.
Riemann Surfaces. Visualization of Riemann Surfaces. From Cusp to Ramification: Friendly Introduction to Riemann Surfaces - David Bai - The Archimedeans. Enjeux de la géométrie non euclidienne.