

Géométrie. La géométrie (du grec ancien : γεωμετρία ; géo- "terre", -métron "mesure") est, avec l' arithmétique , l'une des branches les plus anciennes des mathématiques .
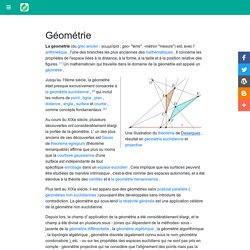
Il concerne les propriétés de l'espace liées à la distance, à la forme, à la taille et à la position relative des figures. [1] Un mathématicien qui travaille dans le domaine de la géométrie est appelé un géomètre . Initiation à la géométrie. Point (géométrie) En plus de définir des points et des constructions liées aux points, Euclid a également postulé une idée clé sur les points, à savoir que deux points quelconques peuvent être reliés par une ligne droite.
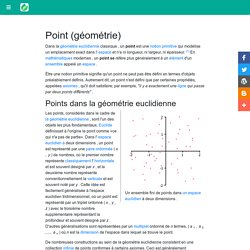
Ceci est facilement confirmé dans les extensions modernes de la géométrie euclidienne, et a eu des conséquences durables lors de son introduction, permettant la construction de presque tous les concepts géométriques connus à l'époque. Cependant, la postulation des points d'Euclide n'était ni complète ni définitive, et il supposait parfois des faits sur des points qui ne découlaient pas directement de ses axiomes, tels que l'ordre des points sur la ligne ou l'existence de points spécifiques. Malgré cela, les extensions modernes du système servent à supprimer ces hypothèses. Dimension de l'espace vectoriel. Plan Euclidien versus Plan Affine - La Saga des Espaces #1. Étienne Ghys - Et si le théorème de Pythagore n'était pas vrai ? "Les Ernest"
MATHSCLIC : PROBLÈME DE NAPOLÉON. Nuits de l'Incertitude #2 - HYPERBOLIQUE - Etienne Ghys et Don Zagier - 2012. Livres de Géométrie. Mathraining. GeometrieAffine. Géométrie Affine. Introduction à la géométrie analytique. Géométrie analytique. Page du p'tit bonhomme. Géométrie Magazines. Géométrie (histoire) Pattern Shapes by the Math Learning Center. Géométrie.
Trigonométrie classique et hyperbolique. Vecteurs. Courbes et Surfaces. Mesure (et théorie de Lebesgue) Lieux géométriques. Perspective. Convexité. Barycentre. Pavages. Fractales "algorithmiques" Réseaux. Géométrie et nombres. Géométrie descriptive. Géométrie projective. Géométrie algébrique. Géométries non euclidiennes. DE LA TOPOGRAPHIE À LA GÉOMÉTRIE I. Cet article paraîtra aussi dans l’ouvrage « La carte invente le monde » de la collection Les nouveaux Rendez-vous d’Archimède, Presses Universitaires du Septentrion, 2017.
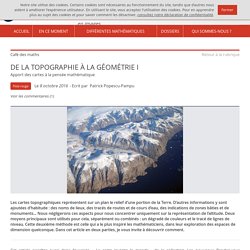
PREMIÈRE PARTIE : Des cartes topographiques à la structure des surfaces Saviez-vous que Paris est une ville à huit collines ? Voici une carte qui permet de le vérifier : La ville aux huit collines. On peut y voir les noms de ces collines, ainsi que leurs altitudes. En voici une autre dans laquelle la collection des lignes d’altitude constante est enrichie par des informations concernant les routes, les bâtiments et les communes : Une carte topographique enrichie d’informations supplémentaires. Comment construit-on une carte de ce type ? Principe de construction d’une carte topographique, illustré à l’aide d’une surface lisse représentant un paysage à deux collines.
Bien sûr, la Terre n’étant point plate, la notion de plan « horizontal » n’est pas bien définie. Quelques réflexions de Cayley Un cratère de volcan. DE LA TOPOGRAPHIE À LA GÉOMÉTRIE II. Cet article paraîtra aussi dans l’ouvrage « La carte invente le monde » de la collection Les nouveaux Rendez-vous d’Archimède, Presses Universitaires du Septentrion, 2017.
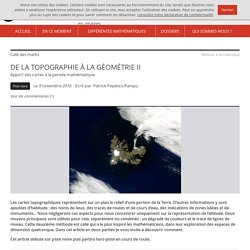
La première partie est accessible ici. DEUXIÈME PARTIE : Vers la théorie de Morse Dans la première partie nous avons comparé deux études du découpage des surfaces par des plans parallèles, celle de Cayley et celle de Möbius. Nous avons vu Möbius en déduire un théorème de classification des surfaces closes de l’espace euclidien de dimension trois, et nous avons reformulé ce théorème de classification en termes de « surfaces en anses ». Enfin, nous avons découvert qu’un théorème analogue a été démontré par Heegaard pour les variétés closes de dimension trois.
Géométrie dynamique. Recherches sur la géométrie dynamique et ses applications pédagogiques, sous la responsabilité d’Yves Martin.

Après avoir travaillé pendant plus de 15 ans avec Cabri-géomètre, rédigé le site abraCAdaBRI qui n’est plus maintenu mais comporte toujours quelques jolis chapitres, le temps des logiciels libres est venu. La formation à l’IUFM s’est adaptée, et ces pages présentent un autre logiciel de géométrie dynamique — et autre que Geogebra — qui a de nombreux atouts pour lui. Il existe en effet plusieurs « grands » logiciels de géométrie dynamique, dont, pour ceux pratiqués en France, la référence historique Cabri-géomètre, toujours excellent, mais qui n’est plus vraiment développé depuis l’arrivée de deux logiciels libres multiplateforme : Geogebra et CaRMetal.
Ces deux derniers sont proposés dans la bibliothèque des logiciels utilisables pour l’agrégation de mathématiques. Les raisons du choix de CarMetal pour cette formation sont de plusieurs ordres : Cours de géométrie élementaire - Accès à l'enseignement supérieur. Similitudes directes, similitudes indirectes - Similitudes directes, similitudes indirectes. Plan passant par 3 points (non alignés)
Voyage en dimensions supérieures - Eva Philippe - MPT17 #8. GÉOMÉTRIE NON COMMUTATIVE ET PHYSIQUE - Institut d'astrophysique de Paris. Comment ce sous-plat peut nous aider à filmer des hobbits ? Structures déployables ou flexibles. Math'@ctivité. Rdasson. Yt00 Mathactivité. Roland Dassonval. Cinema3D. Géométrie - LTHE. 3Mre Geom. Euclidea - Geometric Constructions Game with Straightedge and Compass.
Géométrie - Table des matières. Ligne droite Le chemin le plus court d'un point à un autre est la ligne droite, à condition que les deux points soient bien en face l'un de l'autre.

Math'@ctivité 3D : Flexagone. Le résultat final est un anneau de moebius à la façon d'Escher et il est manipulable.

Il se range dans une pochette d'origami lui servant de présentoir. Ce sont des objets en 3 dimensions (3D) même si le flexagone est applati lorsqu'il n'est pas manipulé. Pour voir le flexagone en action, cliquer sur l'animation ci-contre puis sur le bouton play. Pour voir une autre animation vidéo, cliquer sur l'icône suivante ("V" comme vidéo) puis 2 fois sur le bouton "play" : .
Un point. Les formes de la géométrie et l’universalité des intuitions mathématiques - La vie des formes - Collège de France - 13 octobre 2011 11:15. PV75 Un brin de dynamisme - [APMEP Lorraine] Geom transfos. Livre geometrie. Affiche Les Bornes. Geometrie II. SML. Géométrie. L. Saint-Raymond - Quand les ondes dessinent des motifs géométriques - PeerTube. How to convert a non-math-lover (Dandelin spheres) Pourquoi des plis dans les vêtements? (Amandine Aftalion) TROIS MILLE DEUX CENT SOIXANTE-QUATRE… Une lampe-torche éclaire des zones limitées par des courbes qu’on appelle des coniques.
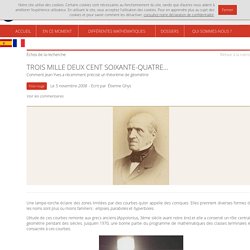
Elles prennent diverses formes dont les noms sont plus ou moins familiers : ellipses, paraboles et hyperboles. L’étude de ces courbes remonte aux grecs anciens (Appolonius, 3ème siècle avant notre ère) et elle a conservé un rôle central en géométrie pendant des siècles. Jusqu’en 1970, une bonne partie du programme de mathématiques des classes terminales était consacrée à ces courbes. Intersection de coniques Deux coniques peuvent se couper en 0, 1, 2, 3 ou 4 points comme le montrent ces figures : Les mathématiciens considèrent que deux coniques se coupent toujours en 4 points, quitte à admettre que certains d’entre eux sont « imaginaires », ou « à l’infini » ou même « multiples » ! Deux (deux?) minutes pour la quadrature du cercle. Cercle d'Apollonius. Construction[modifier | modifier le code] Un exemple de cercles d'Apollonius Les cercles d'Apollonius peuvent être construits comme suit.
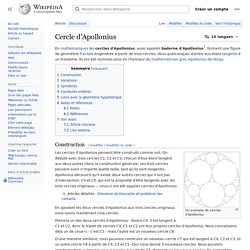
On débute avec trois cercles C1, C2 et C3, chacun d'eux étant tangent aux deux autres (dans la construction générale, ces trois cercles peuvent avoir n'importe quelle taille, tant qu'ils sont tangents). Apollonius découvrit qu'il existe deux autres cercles qui n'ont pas d'intersection, C4 et C5, qui ont la propriété d'être tangents avec les trois cercles originaux — ceux-ci ont été appelés cercles d'Apollonius. En ajoutant les deux cercles d'Apollonius aux trois cercles originaux, nous avons maintenant cinq cercles. Cercle de Ford. Cercles de Ford : Un cercle est posé sur chaque fraction irréductible.
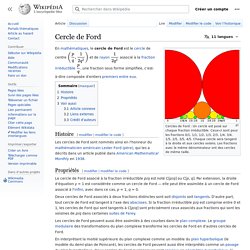
Ceux-ci sont pour les fractions 0/1, 1/1, 1/2, 1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5. Chaque cercle sera tangent à la droite et aux cercles voisins. Escher Marechal. 2ndmathsgeom. Difficultés des élèves dans un problème de démonstration en géométrie. DANS QUELLE FORME LA PLUS PETITE PAROI ENFERMANT UN VOLUME DONNÉ EST-ELLE LA PLUS GRANDE ? Si on note une région du plan, son aire et son périmètre, c’est-à-dire la longueur de son contour, l’inégalité isopérimétrique s’écrit ainsi (Plus de détails dans un billet précédent et dans une vidéo de cinq minutes) Cette inégalité était connue des mathématiciens antiques, et on peut considérer qu’elle a été démontrée rigoureusement dès le XIXe siècle.
Toutefois, il existe de nombreuses variantes sur ce thème, certaines démontrées (par exemple l’inégalité analogue dans l’espace , et même dans les dimensions supérieures), certaines conjecturales. L’inégalité isopérimétrique classique Avant de considérer une des variantes conjecturées les plus simples (et donc les plus frustrantes), essayons d’expliquer pourquoi une telle inégalité est intéressante ; on considèrera une région de forme a priori quelconque en dimension ou , et on parlera dans les deux cas de « périmètre » pour la longueur ou l’aire du contour de , et de « volume intérieur » pour l’aire ou le volume de . Un problème ouvert. L’INÉGALITÉ ISOPÉRIMÉTRIQUE.
L’inégalité isopérimétrique est la solution d’un problème simple à expliquer, pas évident à résoudre, et qui offre une multitude de variantes et de développements. Dans le plan Le problème qui nous intéresse est le suivant : si on dispose d’une corde de longueur fixée, disons , quelle est la plus grande surface qu’on puisse entourer avec cette corde ? On peut par exemple disposer la corde le long d’un carré de côté , et on obtiendra une surface . Mais il paraît plus malin de disposer la corde le long d’un cercle. Rozenn Texier-Picard - Le problème isopérimétrique.
Le théorème du carreleur. Des cristaux et des maths. Des yeux de mouche aux ruches d’abeilles, les structures géométriques des cristaux se retrouvent partout dans la nature. Comment l’expliquer ? La question taraude de nombreux mathématiciens, dont Mathieu Lewin, qui nous éclaire sur ce sujet intrigant. À l’échelle microscopique, la plupart des cristaux sont constitués d’atomes qui sont arrangés sur un réseau périodique, c’est-à-dire suivant des motifs qui se répètent comme des nœuds sur un filet de pêche.
Cette structure géométrique particulière au niveau atomique induit souvent un comportement singulier à notre échelle. Or de telles structures périodiques sont présentes partout autour de nous dans la nature. L’arrangement périodique hexagonal des atomes explique la forme géométrique à six branches de ce cristal de glace. Percer les secrets du réseau hexagonal… Comment expliquer l’omniprésence dans la nature de certains de ces arrangements périodiques particuliers, comme le réseau hexagonal ? … et de l’organisation spontanée de la matière.
QUELQUES PROBLÈMES OUVERTS DE GÉOMÉTRIE ÉLÉMENTAIRE. Le 6 avril 2009 - Ecrit par Jean-Marc Schlenker Lire l'article en La géométrie discrète est une branche des mathématiques qui s’intéresse aux objets géométriques qui sont « discrets », c’est-à-dire qu’ils peuvent être décrits par un nombre fini de paramètres. Elle est relativement peu pratiquée dans les départements de mathématiques de par le monde, mais beaucoup plus dans les départements d’informatique (ou de computer science), où ils intéressent à la fois pour eux-même et pour leur rôle dans des applications. Alors que la plupart des questions de géométrie étudiées par les mathématiciens sont relativement abstraites et difficiles d’accès, la géométrie discrète recèle une multitude de questions remarquablement faciles à poser, mais dont on ne connaît pas la réponse — on parle de problèmes « ouverts ». On va en présenter trois, choisis parmi beaucoup d’autres.
BALLON ROND. Un ballon de football, comme celui que montre le logo de ce billet, est formé de morceaux de cuir (ou d’une autre matière) cousus entre eux. En regardant attentivement [1], on s’aperçoit que tous ces morceaux n’ont pas la même forme. Certains ont cinq côtés, ce sont des pentagones, en noir sur le logo, d’autres en ont six, ce sont des hexagones, en blanc. Il arrive fréquemment (je parle de la vie de tous les jours, pas des mathématiques) que l’on rencontre des hexagones assemblés, par exemple sous forme de « tomettes » de carrelage.
Sur cette image les hexagones s’emboîtent pour recouvrir une surface plane, aussi grande que l’on veut d’ailleurs. Le calcul des tresses(*) - Apmep. Tesseract. Werner Wendelin - "Karl Löwner et les découpages de formes" - 2013. Broué Michel - "Des lois du mariage à Bourbaki" - 2010. Pendant la deuxième guerre mondiale, à New York, le mathématicien André Weil et l'ethnologue Claude Lévi-Strauss, tous deux français réfugiés, se rencontrent. À la recherche de la quatrième dimension. <br> Elise Goujard - La baguette magique d'Eskin-Mirzakhani. DavidCoeurjolly. CoursGeoLicence. Introduction to Noncommutative Geometry. INSMI - Institut national des sciences mathématiques et de leurs interactions - Une version géométrique de la conjecture des périodes. Hilbert Les principes fondamentaux de la Géométrie. IMAGINARY. A. Deledicq - Mathématiques et jubilation: avec quoi, comment, pourquoi ? - PeerTube.
Le théorème des 4 couleurs — Science étonnante #4. Géométrie. EJE: GEOMETRÍA Y MEDIDA. GÉOMÉTRIE. Intro geom lorentzienne02 2007.