

MATHÉMATIQUES : FORMES NORMALES DE CHAMPS DE VECTEUR. Champs de vecteurs :) Rediffusion d’un article publié en octobre 2017 Piste bleue Le 27 mars 2020 - Ecrit par Pierre Monmarché [ Rediffusion d’un article publié en octobre 2017] Savez-vous planter les vecteurs à la mode de chez nous ?
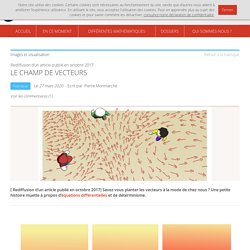
Une petite histoire muette à propos d’équations différentielles et de déterminisme. Quelques explications Remarque : La couleur de piste fonce progressivement.... La notion mathématiques à l’honneur dans cette BD est celle de champ de vecteurs. Ces champs apparaissent dans l’étude des équations différentielles, dont les solutions sont des trajectoires qui suivent le champ de vecteur, c’est-à-dire qu’à chaque instant, l’évolution de la trajectoire (la courbe bleue ci-dessous) est prescrite par la flèche gravée au sol : C’est exactement ce qui se passe pour les personnages de la BD : les vecteurs au sol leur indiquent la direction et la vitesse (plus ou moins grande selon la norme du vecteur) à laquelle ils doivent se déplacer. (en cas de doute, les correspondances sont ici [2]) Notes. Les vecteurs : introduction. Les vecteurs à deux dimensions : introduction.
Propriétés du produit scalaire. Le produit scalaire. Rappels de géométrie, courbes et surfaces - Produit scalaire, produit vectoriel,produit mixte. Repère de Frenet. Math.ing : Un Vecteur, Qu’est-ce que c’est ? - WebTV Université de Lille. Math.ing : les Vecteurs et Galilée - WebTV Université de Lille. Math.ing : les Vecteurs et Newton - WebTV Université de Lille. Réussir ses projections vectorielles en mécanique. Déduire des extrémités - Cas des projections vectorielles. Espaces vectoriels. Cours math sup, math spé, BCPST. Espace vectoriel/Familles de vecteurs. Une page de Wikiversité.
Début de la boite de navigation du chapitre fin de la boite de navigation du chapitre En raison de limitations techniques, la typographie souhaitable du titre, « Espace vectoriel : Familles de vecteurs Espace vectoriel/Familles de vecteurs », n'a pu être restituée correctement ci-dessus. Soient : et deux -espaces vectoriels ; une famille d'éléments de . Familles de vecteurs[modifier | modifier le wikicode] Base d'un espace vectoriel[modifier | modifier le wikicode] Définition[modifier | modifier le wikicode] Début d’un théorème Fin du théorème Base canonique[modifier | modifier le wikicode] Début de l'exemple Fin de l'exemple Changement de bases[modifier | modifier le wikicode] Un vecteur est une entité géométrique. C'est un peu comme si on étudiait une poutre dans un quadrillage d'unité 1 cm et dans un quadrillage d'unité 5,27 dm. Espaces vectoriels. Structure d'espace vectoriel. Soit (K,+,×) un corpscommutatif d'élément unité noté 1.

On nomme espace vectoriel sur K, (on dira aussi un K-espace vectoriel) un groupe abélien (E,+) muni d'une seconde loi dite externe, application de K ×E dans E notée ici par un simple point (.), que l'on peut omettre s'il n'y a pas d'ambiguïté, et vérifiant les axiomes suivants : Si x et y désignent des éléments (on pourra dire vecteurs) de E, a et b désignant des scalaires : On notera (E,+, .) un tel espace vectoriel.
Par opposition aux vecteurs de l'espace E, les éléments de K, jouant le rôle de nombres (généralement K = R ou C), sont appelés scalaires (du latin scala = escalier, échelle, degré, au sens ici d'échelle de valeurs). La loi externe est souvent appelée multiplication scalaire car elle fait fait intervenir les éléments de K. Lorsque K est un anneau commutatif et unitaire, sans être un corps, on parle de module (le terme est dû à Dedekind) au lieu d'espace vectoriel. a .x + b . y + c . z + ... a, b, c, ... éléments de K. Topologie générale. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Les progrès de l'analyse, dans l'étude des fonctions continues (naïvement : dont la représentation graphique n'a pas de trous), de leur dérivabilité, de leurs limites en un point (fini ou non), de l'existence d'extremums, demandaient une définition rigoureuse de l'idée intuitive de proximité, tout particulièrement lors d'opérations sur ces fonctions.

Les suites de fonctions et la "découverte" de la convergence uniforme nécessitèrent de nouveaux outils. On travaille là dans des ensembles dont les points (éléments) sont des fonctions : espaces fonctionnels. Le terme actuel de topologie est dû à Listing. Mot à mot, la topologie est la science des lieux (du grec logos = discours au sens discursif : étude, raisonnement et topos = lieu, site). ➔ La continuité n'est pas l'apanage de l'analyse. Pdf ma100 poly algebre lineaire 4. Espaces vectoriels. 2019CAPEMCOURSEVN. Algèbre linéaire & multilinéaire.