

Est-ce mal de montrer une courbe dont l’axe des ordonnées ne démarre pas à zéro ? La semaine dernière, j’ai publié une vidéo dont le but était d’examiner la physique qui se trouve derrière le réchauffement climatique.

J’ai évidemment eu droit à une horde de commentaires climatosceptiques, dont je n’ai que faire puisque la vidéo ne s’adressait pas à eux : je l’avais plutôt faite pour toucher les « climato-agnostiques », ceux qui ne savaient pas trop quoi penser de tout ça et qui pouvaient avoir des doutes sur les fondements scientifiques du phénomène, ou sur l’opacité des modèles climatologiques. Mais ça n’est pas de ça dont je veux vous parler aujourd’hui ! Je voudrai plutôt revenir sur une remarque qui m’a été faite plusieurs fois en commentaire (sans malveillance généralement) : le fait que ma courbe d’évolution du CO2 ait une ordonnée qui ne démarre pas à zéro.
Voici la courbe en question : Alors est-ce que c’est mal de faire une courbe avec l’ordonnée qui ne démarre pas à zéro ? Two dimensional curves. Voyage au bout du tore.
Coniques et quadriques. Courbes et surfaces paramétrées. Enveloppe convexe d'une famille de courbes. Surfaces. Courbure. Le déplacement d'une Dictyostelium discoideum dont la couleur du contour est fonction de la courbure.
Échelle : 5 µm ; durée : 22 secondes. Intuitivement, courbe s'oppose à droit : la courbure d'un objet géométrique est une mesure quantitative du caractère « plus ou moins courbé » de cet objet. Par exemple : dans le plan euclidien, une ligne droite est un objet à une dimension de courbure nulle et un cercle un objet de courbure constante positive, valant 1/R (inverse du rayon) ;dans l'espace euclidien usuel à trois dimensions, un plan est un objet à deux dimensions de courbure nulle, et une sphère est un objet à deux dimensions de courbure constante positive. Une « selle de cheval » possède au contraire un point de courbure négative.
Demos for gnuplot version 5.2. Courbetsurface. Courbes Surfaces. Chap1 courbes étude locale. CSPolyL3. CoursCS3. CoursMT25 P07. Cours M1. Cours courbes et surfaces l3. Interpolation numérique – TITANE Inria project-team. L’interpolation et l’approximation sont deux notions fondamentales pour l’analyse et le traitement des données.
Ce cours offre une introduction à ces notions et à leurs applications, partant de représentations géométriques continues des données, et évoluant progressivement vers l’analyse et le traitement des données par des méthodes géométriques. L’interpolation de distributions de données sera abordé sous l’angle du transport optimal. Les concepts et algorithmes de ce cours seront motivés par de nombreuses applications pratiques, et illustrés par des exercices sur table et de la programmation sur machine (C++ et/ou Matlab). Programme Interpolation Approximation (régression) Analyse en composante principale: définitions, optimalité, algorithmes, interprétation géométrique.Surfaces discrètes: maillages, estimation de mesures différentielles.Surfaces de subdivisionDétection de structures: transformée de Hough, RANSAC, clustering, symétries et orbites.
Supports de cours: Courbe. Courbes planes. Courbes gauches. Courbes bezier. Cours surfaces part1. Cours surfaces part2. Courbes, surfaces, leur beautée géométrique ! m3ds courbe. Class3a. Courbes et surfaces gauches - Ecole Nationale Supérieure d ... Virtual Math Labs: Curves and Surfaces. Visualization in Geometric Knot Theory A jReality application realizing different interactive visualizations in geometric knot theory. load, edit and save knots explore the crossing map of a given knot analyze the set of trisecants of a given knot and find quadrisecants create images of textured knots.
Changing Views on Curves and Surfaces - Kathlén KOHN. Confinement 08 04 2020. VISUALISER LA COURBURE. Comprendre la notion de courbure sans aucune formule...

Du simple rayon de courbure jusqu’au tenseur de Riemann, clé de voûte de la géométrie différentielle. Panorama non exhaustif ! « La géométrie est la science des raisonnements corrects sur des figures incorrectes », George Pólya, How to solve it, Princeton 1957. [1] Certaines notions géométriques semblent très intuitives. Habitués que nous sommes à notre expérience sensorielle, les représentations visuelles nous guident parfois habilement dans la compréhension de concepts géométriques. L’exemple que nous allons développer ici est celui de la courbure. Le mathématicien étudie souvent des objets ou des espaces si complexes que toute représentation visuelle serait une tentative futile, vouée à l’échec. UN THÉORÈME ET UNE PART DE PIZZA. Dans cet article, nous proposons de comprendre l’énoncé de cet important théorème de Gauss, que tout étudiant de fin de licence apprend en cours de géométrie des surfaces.
Voici son énoncé : Théorème Remarquable (ou Theorema Egregium) Deux surfaces de classe localement isométriques ont la même courbure de Gauss en tout point. Pour le comprendre, il nous faut d’abord se familiariser avec les notions d’isométrie et de courbure de Gauss. Par chance, ces notions sont très intuitives. Allons-y ! Surfaces isométriques Qu’est-ce qu’une surface ? Déjà, qu’est-ce qu’une surface ? Un morceau de feuille de papier est une surface, tout comme la surface d’une orange à laquelle on aurait retiré l’intérieur (une sphère).
Une surface de classe est une surface qui a en plus la propriété d’être « assez lisse ». Une feuille de papier tout juste sortie de sa ramette, éventuellement légèrement courbée, est une surface lisse. Ces courbes qui colorient tout l'espace. Les courbes remplissantes (ou comment faire un coloriage avec un crayon ponctuel) Ma fille n’aime pas quand les crayons de couleur sont taillés trop fins.
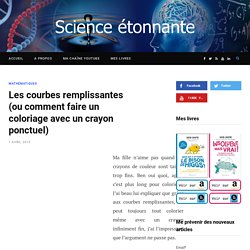
Ben oui quoi, après c’est plus long pour colorier ! J’ai beau lui expliquer que grâce aux courbes remplissantes, on peut toujours tout colorier même avec un crayon infiniment fin, j’ai l’impression que l’argument ne passe pas. Et pourtant, nous allons voir dans ce billet que l’on peut effectivement trouver des courbes qui remplissent totalement une surface en passant par tous ses points. Et tant pis si ça va à l’encontre de l’intuition ! Pourquoi cela nous parait impossible Alors allons-y, essayons de relever le défi : trouver une courbe qui colorie complètement un carré. D’ailleurs, une courbe est un objet de dimension 1, alors qu’un carré est de dimension 2. La construction de Cantor A la fin du XIXème siècle, le mathématicien allemand Georg Cantor a décidé de s’attaquer à la notion d’infini (voir à ce sujet cet épisode de Podcast Science).
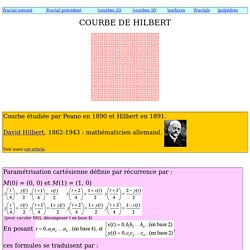
Les courbes fractales de Peano. Courbe de Hilbert. Définition n°1 : La courbe de Hilbert est l'unique courbe de Peano binaire remplissant le carré [0, 1]2 et telle que M(0) = (0, 0) et M(1) = (1, 0).Elle est donc définie par l'algorithme : 1) Partager [0, 1]2 en 4 "petits" carrés "égaux" ; numéroter chacun de ces carrés de sorte que deux carrés successifs se touchent par un côté, en commençant par le carré en bas à gauche, et terminant par le carré en bas à droite. 2) Partager chacun de ces carrés en 4 "micro" carrés "égaux" ; numéroter chacun de ces carrés de sorte que deux micro carrés successifs se touchent par un côté, en commençant par le micro-carré en bas à gauche, et terminant par le micro-carré en bas à droite, le premier micro-carré d'un petit carré devant avoir un côté en commun avec le dernier micro-carré du petit carré précédent et le dernier micro-carré devant toucher par un coté le petit carré suivant. 3) Recommencer ce processus à l'infini.
Courbe d'ordre Z — Wikipédia. eVa en tore-carré. Apostrophe à un fanfaron « Nash, si tu es si bon, pourquoi ne résous-tu pas le problème du plongement isométrique des variétés riemanniennes ?
[1] » L’homme qui ose ainsi défier le futur prix Nobel d’économie [2] n’est autre que son voisin de bureau, Warren Ambrose. Nous sommes en 1953 au laboratoire de mathématique du MIT et Ambrose, excédé par les incessantes rodomontades de John Nash — qu’il surnomme « Gnash » [3] — est bien décidé à donner une leçon de modestie à ce jeune et impétueux mathématicien. Au-delà des termes techniques, le problème qu’il lui lance possède une réputation à décourager les plus téméraires. ROTHORN, UN TORE PLAT ! Piste verte Le 17 décembre 2012 - Ecrit par Aurélien Alvarez Lire l'article en Faites-vous offrir un survol du tore plat par Rothorn !
À la fin du printemps, Images des maths consacrait sa rubrique Objet du mois à un tore plat. Cet objet paradoxal, inventé abstraitement il y a presque soixante ans, venait tout juste d’être visualisé. Bouteille de Klein. Vue de la bouteille de Klein dans un espace à trois dimensions. Construction[modifier | modifier le code] Voici un plan de montage dans ℝ3. À partir du carré initial, on colle les deux bords rouges l'un contre l'autre, dans le sens des flèches. La figure obtenue est un cylindre, dont on veut identifier les deux bords à l'aide des flèches bleues. Pour respecter le sens de ces flèches, il est nécessaire de retourner l'un des cercles avant de le recoller à l'autre, et pour cela, d'opérer une auto-intersection.
PYTHAGORE ET LES COURBES DE PÓLYA. Le théorème de Pythagore est enseigné dans les collèges français. Il affirme que, dans un triangle à angle droit, la somme des carrés des petits côtés est égale au carré du grand côté (l’hypoténuse) ; ce théorème peut être démontré de bien des façons, l’une d’entre elles étant donnée dans un article précédent de cette rubrique.
Nous allons en voir une seconde, plus complexe, qui nous conduira vers une famille de courbes très spéciales construites par le mathématicien George Pólya en 1913. [1] Pythagore Considérons donc un triangle avec un angle droit, et notons , et les longueurs des trois côtés de ce triangle, avec , si bien que correspond à l’hypoténuse. En abaissant la hauteur qui s’appuie sur l’hypoténuse, on découpe le triangle initial en deux triangles plus petits que nous noterons et : est le plus petit des deux triangles, le plus grand. Cours de maîtrise de math, M.M.D. B.2.: Courbes, surfaces et sous-variétés. On trouvera ici, mise en ligne suivant l'avancement du cours, mes notes personnelles - incomplètes, les énoncés des devoir, ainsi que quelques sujets d'examen des années précédentes. Syllabus, au format ps ou pdf. Texte complet, chapitres 1 à 6, au format ps ou pdf.
Courbes et courbure. Courbes et surfaces. Le nouvel objet le plus satisfaisant du monde ! (ZipString) Surfaces de Riemann cours manuscrit J-P Demailly.