

Surfaces. Geometry: Gallery of Surfaces. Complementary surfaces(spheres and tears) La classification des surfaces via la théorie de Morse : 1ère partie. La classification des surfaces via la théorie de Morse : 2ème partie. La classification des surfaces via la théorie de Morse : épilogue.
Bulles de savons et surfaces minimales. Surfaces 3d. Plan tangent. Géo diff Variétés ... Courbes et surfaces paramétrées. Surfaces algébriques. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Au 19è siècle, on avait déjà de l'humour... : un dessin de Cham, caricaturiste français (1819-1879) Encyclopédie Larousse méthodique (1955) → Généralités : En dehors de l'acception courante, synonyme d'aire (en toute rigueur une aire est la mesure d'une surface), la notion mathématique de surface en tant qu'ensemble de points de l'espace (assimilé à R3), est fort complexe. ➔ Écoliers, collégiens, noter d'ores et déjà que surface ne signifie nullement plat.

Une feuille de papier est une surface, elle le reste si elle est chiffonnée ! La théorie des surfaces a été tout particulièrement étudiée par Monge en France, puis Gauss et Riemann en Allemagne, ce dernier se dégageant de l'aspect purement euclidien. Surfaces et tableaux de Young. Surfaces. Voir les notations ci-dessous.
Surfaces commençant par ANSES (SURFACE À n/) HYPERSPHÈRE (de dimension 3, de dimension n) PENTE (LIGNE DE/, ou LIGNE DE PLUS GRANDE/) Sn SPHÈRE DE DIMENSION n. Mathematical models. Algebraic geometry - Interesting implicit surfaces in $\mathbb{R}^3$ Rappels de géométrie, courbes et surfaces - Surfaces-Courbes dans l'espace-Equations. Surfaces particulières. Surfaces de révolution. Préliminaires Nous considérons une courbe paramétrée telle que définie ici : t → M(t)(x(t),y(t),z(t)) où t parcourt un intervalle I de ℝ et où pour tout t ∈ I le point M(t) reste dans un même plan.

Si nous effectuons maintenant une rotation d'une telle courbe autour d'un axe, que se passe-t-il ? Il est clair que la courbe est transformée en une autre courbe plane située dans un autre plan se déduisant du premier par la rotation. Traitons le problème analytiquement dans un repère orthonormé (O, →u,→v,→w) où →w est un vecteur directeur de l'axe de la rotation. Soit θ l'angle de la rotation relativement à l'axe orienté par →w. Définitions Une 'surface de révolution' S est la partie de l'espace engendrée par la rotation d'une courbe paramétrée plane C autour d'un axe Δ.
Surfaces réglées. Cette page se résume à quelques définitions.

Nous ne proposons aucun résultat, il s'agit simplement d'accroître la 'bibliothèque' du lecteur en matière de figures de l'espace qui se résume pour l'instant : Aux variétés linéaires (points, droites, plans) Aux sous-ensembles de telles variétés (segments, demi-droites, demi-plans, etc...) Aux sphères A quelques polyèdres (tétraèdres, parallélépipèdes) Les figures que nous allons définir dans cette page et la suivante permettent d'enrichir notablement cette collection. En outre, nous utiliserons abondamment ces figures dans le prochain chapitre consacré aux coniques.
Courbes planes. Sections planes de surfaces (enseignement de spécialité) : fiche de synthèse et exercices d'application directe - Sections planes de surfaces (enseignement de spécialité) : fiche de synthèse et exercices d'application directe. From Wolfram MathWorld. Del Pezzo Surfaces. Trièdre de Darboux-Ribaucour. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Considérons une surfaceΣ définie par la donnée des coordonnées gaussiennes x, y et z de ses points : x = f(u,v) , y = g(u,v) , z = h(u,v) On suppose que x, y et z sont des fonctions au moins deux fois continûment dérivables en u et v (classe C2) et que la normale à la surface est bien définie dans un voisinage V d'un point M (point non singulier).

Mobius Parpay. Principes fondamentaux de la théorie des pseudo-surfaces : Issaly, abbé, (Pierre-Adolphe), b. 1833 : Free Download, Borrow, and Streaming. Formes bilinéaires, quadratiques, courbes, surfaces... [Conférence] M. LHUISSIER - Alicia Boole Stott - Géomètre oubliée de la quatrième dimension. Rappels de géométrie, courbes et surfaces - Plan tangent à une surface, droite tangente à une courbe de l'espace.
Cubic surfaces - MacTutor History of Mathematics. Nombre d'Euler. Christian RONSE © (02/11/2007) LSIIT UMR 7005 CNRS-ULP, Département d'Informatique de l'ULP Le Nombre d'Euler est un entier associé à toute surface orientable.

C'est un invariant topologique de celle-ci, dans le sens qu'il ne change pas si la surface subit une déformation continue. Il est obtenu comme suit : on trace un graphe planaire connexe sur la surface, ayant S sommets, A arêtes, et F faces ; le nombre d'Euler est alors l'entier Ce nombre ne dépend pas du choix du graphe planaire. Dans le cas où la surface est une figure incluse dans le plan euclidien R2, ce nombre est égal au nombre de composantes connexes de la figure moins le nombre de trous. Paradoxes mathématiques. Voici pour vous faire économiser de la peinture ou dépenser une fortune à Bricomarché, selon votre manière de peindre...

Empilons des cubes évidés de côté a/√n pour n ≥ 1. Le volume obtenu pour les N premiers cubes est ∑n=1Na3/n√n̅, or cette suite converge quand N → ∞ vers une limite a3ζ(3/2) = a3∑n=1∞1/n3/2. On peut donc remplir la structure obtenue. Mais imaginons d'en peindre les faces internes : pour N cubes, il faudrait 4a2∑n=1N1/n [1], or cette quantité tend vers... +∞. Il y a paradoxe : on ne peut pas peindre, mais on peut remplir de peinture... RECREATIONS GEOMETRIQUES. Représentation polyédrique d'un point cuspidal, calcul de sa courbure concentrée.

Représentations polyèdriques de différentes surfaces. Permutation des points cuspidaux d'une Cross cap. Transformation d'une surface de Boy "droite" en surface de Boy "gauche", via la surface Romaine de Steiner. Inversion "droite"-"gauche" d'une surface de Boy. IMAGINARY. Mathématiquement, le programme illustre la géométrie algébrique réelle en temps réel.
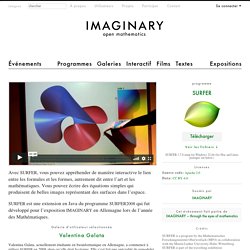
Les surfaces exhibées sont obtenues comme l’ensemble des zéros d’une équation polynomiale en les variables x, y et z. Tous les points de l’espace qui résolvent l’équation sont représentés et forment la surface. Regardez par exemple x2+y2+z2-1=0, l’équation de la sphère. Coeur avec surfer. Goursat tangle avec SURFER. Des formes pré enrengistrée avec surfer. Ricci Flow. GNASH, UN TORE PLAT ! Apostrophe à un fanfaron « Nash, si tu es si bon, pourquoi ne résous-tu pas le problème du plongement isométrique des variétés riemanniennes ?
[1] » L’homme qui ose ainsi défier le futur prix Nobel d’économie [2] n’est autre que son voisin de bureau, Warren Ambrose. Nous sommes en 1953 au laboratoire de mathématique du MIT et Ambrose, excédé par les incessantes rodomontades de John Nash — qu’il surnomme « Gnash » [3] — est bien décidé à donner une leçon de modestie à ce jeune et impétueux mathématicien.
AtelierD20. CompuTopo3. 3D polyhedron. Geometric Flows of Curves in Shape Space for Processing Motion of Deformable Objects. GenreGraphe. Revetements. Maps. HomotopieCourbes. Persistance pres. Persistance homol. Persistance. 97a. Somme connexe de deux surfaces. SOMME CONNEXE DE DEUX SURFACESConnected sum of two surfaces, zusammenhängende Summe zweier Flächen La somme connexe de deux surfaces;connexes et est la surface, définie à homéomorphisme près, obtenue en retirant un ouvert homéomorphe à un disque à chacune des surfaces, et en identifiant les bords ; notation : , voire 2S pour la somme de deux surfaces homéomorphes. LE RETOURNEMENT DE LA SPHÈRE. Retournement du tore. De quoi parle-t-on ? La topologie étudie les figures à déformations près. Par exemple, vous pouvez déformer une tasse en un tore plein ; un « mug » en un « doughnut » chez les anglo-saxons.
Comme dans l’animation ci-contre à gauche, tirée de la Wikipédia anglophone. Nous parlons bien de déformer des figures dans le plan ou dans l’espace, pas des objets physiques : pour transformer une tasse en beignet on aurait bien des problèmes, ne serait-ce que parce que la matière qui la compose est rigide, chimiquement distincte de celle du beignet, et même leurs masses diffèrent. Pour les figures correspondantes, c’est plus facile, on peut faire ça dans sa tête ou en dessinant, ou même avec de la pâte à modeler (cette dernière nous oblige à conserver le volume). The Cubic Surfaces DVD. What is this? Hypersurface. Thesis Hypersurfaces cubiques (David Madore) Surfaces Dr Scott Schaefer 1 Types of Surfaces.