

Fondation Vasarely - Aix-en-Provence - Centre architectonique - France. VICTOR VASARELY est un plasticien tout à fait singulier dans l’histoire de l’art du XXème siècle.
Accédant à la notoriété de son vivant, il se distingue dans l’art contemporain par la création d’une nouvelle tendance : l’art optique. Son œuvre s’inscrit dans une grande cohérence, de l’évolution de son art graphique jusqu’à sa détermination pour promouvoir un art social, accessible à tous. Victor Vasarely naît à Pécs en Hongrie en 1906. En 1925, après son baccalauréat, il entreprend de brèves études de médecine à l’université de Budapest, qu’il abandonne deux ans plus tard. De cette période, Vasarely a gardé une volonté de méthode, d’objectivité, une soif de connaissance…proche du monde scientifique. En 1929, il entre au Muhëly, connu comme étant l’école du Bauhaus de Budapest. A cette époque, le gouvernement hongrois commence à associer les différents mouvements avant-gardistes au mouvement progressiste qui se développait en politique. Vasarely.
Pelé: droites concourantes ! Freaky Dot Patterns - Etranges motifs avec des points. Beauté géométrique! Stromae - son album, Racine carrée. Triangle ("impossible") de Penrose. La chute d'eau d'Escher : le mouvement perpétuel en vidéo ! Je voulais évoquer dans cet article les liens entre les dessins d'Escher, la cristallographie et la topologie mais je suis tombé sur une vidéo plutôt bien faite qui m'a détourné de l'objectif initial.
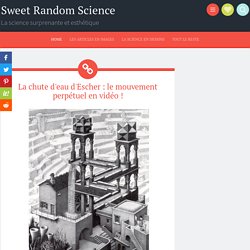
Je garde donc en réserve les vecteurs, les symétries, les atomes et les pavages de Penrose pour la prochaine fois ! La chute d'eau d'Escher Vous connaissez très probablement ce dessin où le graveur néerlandais, obsédé par les figures géométriques, les déformations et les boucles infinies, joue avec la perspective pour créer un cours d'eau perpétuel. Voici sa reproduction en "vrai", je vous laisse vous torturer les méninges pour comprendre le truc. Indice: pas de système de pompe, tout n'est qu'illusion.
Je voulais évoquer dans cet article les liens entre les dessins d'Escher, la cristallographie et la topologie mais je suis tombé sur une vidéo plutôt bien faite qui m'a détourné de l'objectif initial. La chute d'eau d'Escher. Easy 3D Drawing Illusions to Test Your Brain! CES CYLINDRES QUI RENDENT FOU ! (cylindre ambigu) Les 5 solides de Platon - Micmaths. Le flexaèdre - Micmaths. Les hexaflexagones - Micmaths. Hexaflexagones : la multiplication des faces - Micmaths. Contortionist cubes. G-conjecture - Numberphile. The cube shadow theorem (pt.1): Prince Rupert's paradox. The cube shadow theorem (pt.2): The best hypercube shadows. Faire un tétraèdre en tickets de métro - Origami géométrique. Étoiles géométriques en origami - Micmaths. Paper Planes - How to make a Paper Airplane that Flies Far - Best Paper Airplane Tutorial.
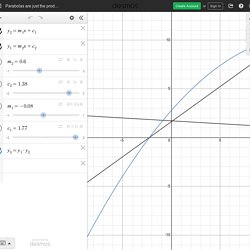
Maryam Mirzakhani: A Tenacious Explorer of Abstract Surfaces. Batman Equation - Numberphile. Parabolas are just the product of straight lines. Parabolas are just the product of straight lines Create AccountorSign In «1x» «2x» «0.35x» «0.5x» powered by powered by functions $$π Create AccountorSign In to save your graphs!
+ New Blank Graph. Beauty of Geodesics. How to convert a non-math-lover (Dandelin spheres) Essence of calculus, chapter 11. Hilbert's Curve: Is infinite math useful? La fourmi de Langton — Science étonnante #21. Le Jeu de la Vie — Science étonnante #49. Epic conway's game of life. Amazing Graphs - Numberphile. Epicycles de Ptolémée. Epicycles de Ptolémée Pour les grecs depuis Aristote (−385, −322) la Terre était le centre du Monde.
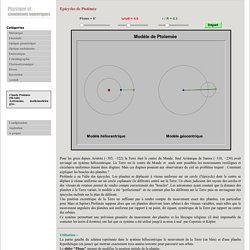
Seul Aristarque de Samos (−310, −230) avait envisagé un système héliocentrique. La Terre est le centre du Monde et seuls sont possibles les mouvements rectilignes et circulaires uniformes étaient deux dogmes. Mais ces dogmes posaient aux observateurs du ciel un problème majeur : Comment expliquer les boucles des planètes ? Ptolémée a eu l'idée des épicycles. Utilisation : La partie gauche du schéma représente dans le système héliocentrique le mouvement de la Terre (en bleu) et d'une planète hypothétique (en jaune) qui mettrait exactement trois années terrestre pour parcourir son orbite.
Le slider rouge permet de modifier le rapport des vitesses de rotation entre l'épicycle et le déférent. Le slider vert permet de modifier le rayon de l'épicycle. Le bouton [Départ] permet de lancer l'animation la pause et la reprise de l'animation.. Un point qui tourne sur un cercle qui tourne sur un cercle qui...El Jj. Pure Fourier series animations for 12 oddly satisfying minutes. But what is a Fourier series? From heat flow to circle drawings. What is a Fourier Series? (Explained by drawing circles) - Smarter Every Day 205. Epicycles, complex Fourier series and Homer Simpson's orbit.
La trajectoire d'un arbitre de foot - Micmaths. Deux (deux ?) minutes pour... le théorème de Bézout. Excourbes. Coordonnées polaires. Pour les articles homonymes, voir Polaire.
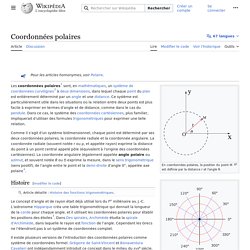
En coordonnées polaires, la position du point M est définie par la distance r et l'angle θ. Un cercle découpé en angles mesurés en degrés. Comme il s’agit d’un système bidimensionnel, chaque point est déterminé par les coordonnées polaires, qui sont la coordonnée radiale et la coordonnée angulaire. La coordonnée radiale (souvent notée r ou ρ, et appelée rayon) exprime la distance du point à un point central appelé pôle (équivalent à l’origine des coordonnées cartésiennes).
La coordonnée angulaire (également appelée angle polaire ou azimut, et souvent notée t ou θ) exprime la mesure, dans le sens trigonométrique (sens positif), de l’angle entre le point et la demi-droite d’angle 0°, appelée axe polaire (équivalente à l’axe des abscisses en coordonnées cartésiennes). Histoire[modifier | modifier le code] Il existe plusieurs versions de l’introduction des coordonnées polaires comme système de coordonnées formel.
Cercle[modifier | modifier le code] et . Tracés animés. Tracés animés vous permet de tracer des courbes et des surfaces, en 2D ou 3D, qui peuvent se zoomer, se déformer et tourner dans tous les sens.
Démonstration. Pour animer vos courbes et surfaces, il vous suffit d'utiliser un paramètre, s. Ce paramètre aura la valeur 0 au début d'une séquence d'animation. Ensuite il va augmenter régulièrement pour s'approcher de 1 à la fin de la séquence. Pierre Deligne : La notion d'espace en mathématique. A Miraculous Proof (Ptolemy's Theorem) - Numberphile. Visualising Pythagoras: ultimate proofs and crazy contortions. Pentagons and the Golden Ratio - Numberphile. Essence of linear algebra, chapter 1. Linear combinations, span, and basis vectors. Essence of linear algebra, chapter 6. Cramer's rule, explained geometrically. Who cares about topology? (Inscribed rectangle problem) Euler's Formula and Graph Duality. Circle Division Solution.
Deux (deux ?) minutes pour... le théorème des 4 couleurs. A Colorful Unsolved Problem - Numberphile. Comment partager un gâteau avec un compas et une règle non graduée! Problème de "lacets" apparemment très simple! théorème de Jordan. Problème d'éclairage! Connexité. Pourquoi vous avez moins d'amis que vos amis - Micmaths. Théorie des graphes. Graphes d'intervalles. Graphes. The mathematical soul of juggling. How not to Die Hard with Math. Math in the Simpsons: the river crossing puzzle cube. The Dollar Game - Numberphile. Un bug géométrique dans Google Map ? - Micmaths. Why is pi here? And why is it squared? A geometric answer to the Basel problem.
The secret of the 7th row - visually explained. Gauss's magic shoelace area formula and its calculus companion. New Reuleaux Triangle Magic. The fix-the-wobbly-table theorem. (3) The hardest problem on the hardest test. Deux (deux?) minutes pour la quadrature du cercle. Quadratures! Unexpected Shapes (Part 1) - Numberphile. Unexpected Shapes (Part 2) - Numberphile. Round Peg in a Square Hole - Numberphile. Hypertwist: 2-sided Möbius strips and mirror universes. 10 Amazing Paper Tricks! Klein Bottles - Numberphile. The man with 1,000 Klein Bottles UNDER his house - Numberphile.
Cut Klein bottles and topological music. Can you solve THE Klein Bottle Rubik's cube? A mirror paradox, Klein bottles and Rubik's cubes. How to put a Rubik's cube in a bottle.