

Coniques (Annexe 1 de la Mécanique de José Philippe Pérez) Outils mathématiques pour la physique (PCSI)/Coniques — Wikiversité. Début de la boite de navigation du chapitre fin de la boite de navigation du chapitre En raison de limitations techniques, la typographie souhaitable du titre, « Outils mathématiques pour la physique (PCSI) : Coniques Outils mathématiques pour la physique (PCSI)/Coniques », n'a pu être restituée correctement ci-dessus.
Sommaire. Les coniques. Unice.fr Les premiers travaux significatifs sur les coniques remontent à Euclide d'Alexandrie (-320?
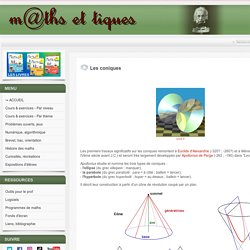
; -260?) Et à Ménechme (milieu du IVème siècle avant J.C.) et seront très largement développés par Apollonius de Perge (-262 ; -190) dans "Les coniques". Apollonius étudie et nomme les trois types de coniques : - l'ellipse (du grec elleipein : manquer), - la parabole (du grec parabolê : para = à côté ; ballein = lancer), - l'hyperbole (du grec huperbolê : huper = au dessus ; ballein = lancer).
Coniques : ellipses, paraboles, hyperboles. Cours complet. Cours prépa scientifique : la réduction des coniques. Remédiation: Détermination des caractéristiques d'une conique (ellipse) Remédiation: Détermination d'une conique (Hyperbole) Les coniques. Trajectoires balistiques dans le système solaire. Auteur : Alain Vienne On considère une sonde spatiale qui se déplace dans le système solaire.
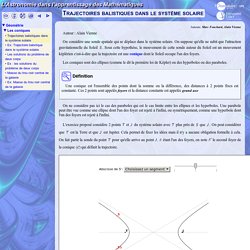
On suppose qu'elle ne subit que l'attraction gravitationnelle du Soleil . Sous cette hypothèse, le mouvement de cette sonde autour du Soleil est un mouvement képlérien c'est-à-dire que la trajectoire est une conique dont le Soleil occupe l'un des foyers. Conics in the cone. UN PLANIMÈTRE À CÔNE. Parmi les machines mathématiques qui furent exposées, on trouve ce magnifique planimètre à cône, remontant au dix-neuvième siècle.
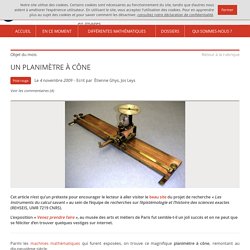
Il permet de mesurer l’aire sous une courbe, comme nous allons l’expliquer ici. Bien sûr, on n’en trouve plus dans les bureaux d’étude d’aujourd’hui ! D’autres planimètres bien plus efficaces ont été inventés par la suite et à l’avenir nous ne résisterons probablement pas au plaisir d’en décrire d’autres pour Images des Maths. Mais son fonctionnement, si simple et si astucieux, permet une meilleure compréhension des concepts d’aire et d’intégrale. Aujourd’hui, pour mesurer la superficie de son jardin, il suffit d’utiliser google maps sur ce site. Voici une courbe, qui est le graphe d’une certaine fonction définie sur un certain intervalle .
On la suppose tracée sur une feuille de papier et on se propose de calculer mécaniquement l’aire de la zone sous la courbe, représentée en bleu sur la figure. Mathématiques : qu’est-ce qu’une conique ? Les coniques ont été étudiées de façon purement gratuite dans l'Antiquité, mais se trouvèrent au centre de la mécanique céleste avec les découvertes de Newton.
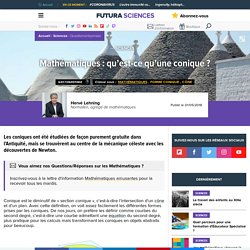
Conique est le diminutif de « section conique », c'est-à-dire l'intersection d'un cône et d'un plan. Avec cette définition, on voit assez facilement les différentes formes prises par les coniques. De nos jours, on préfère les définir comme courbes du second degré, c'est-à-dire une courbe admettant une équation du second degré, plus pratique pour les calculs mais transformant les coniques en objets abstraits pour beaucoup.
Les coniques. Identifier une conique à partir d'une équation (hyperbole) Thomaths 11 : Les Coniques. Les coniques, une grande famille. Pourquoi met-on dans la même famille des courbes aussi différentes que les ellipses, les paraboles et les hyperboles?

Une première réponse est que ce sont des courbes obtenues comme section d’un cône par un plan1. Mais les liens familiaux entre ces courbes sont bien plus forts que cela. Par exemple, toutes ces courbes sont solutions du problème de Kepler : si une planète a une vitesse suffisante, alors elle parcourra plutôt une hyperbole ou encore une parabole avec le Soleil à un foyer. Mais encore… f8ddd7a7e90ea67e0f68164e35f6abc3. Coniques. Coniques Jean-Marc Decauwert Télécharger le fichier pdf.

Coniques à centre. Descartes et les Mathématiques Constructions géométriques des coniques bifocales.

E. Conic Sections Animated Gifs. Gif 1.
Excentricité (mathématiques) Un article de Wikipédia, l'encyclopédie libre.
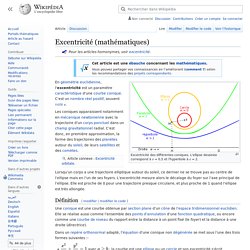
Excentricité des différentes coniques. L'ellipse dessinée correspond à e = 0,5 et l'hyperbole à e = 2. Les coniques apparaissent notamment en mécanique newtonienne avec la trajectoire d’un corps ponctuel dans un champ gravitationnel radial. C’est donc, en première approximation, la forme des trajectoires des planètes autour du soleil, de leurs satellites et des comètes. Ellipses, paraboles, hyperboles : les propriétés des trajectoires en gravitation.
Coniques : foyers & directrices. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Les célèbres coniques (ellipse, parabole, hyperbole) étudiées par les mathématiciens grecs de l'antiquité (Apollonis de Perge, Menechme, Pappus) peuvent être définies au moyen d'un point appelé foyer (Kepler) et d'une droite (d) dite directrice (Pappus). Ainsi, une conique est l'ensemble des points M tels que MF/MH = e où H désigne la projection orthogonale de M sur (d) et e un nombre strictement positif donné. Ce nombre e est appelé excentricité de la conique. La perpendiculaire à (d) passant par F est l'axe focal : il s'agit là de la droite (KF), K désignant la projection orthogonale de F sur (d). Alloprof LES CONIQUES. La parabole (conique) L'hyperbole (conique) Alloprof (L'ellipse) Coniques. Coniques Jean-Marc Decauwert Télécharger le fichier pdf.
Les coniques. Apollonios de Perga. Première édition imprimée des Coniques (livres I à IV), 1537 Biographie[modifier | modifier le code] Apollonius serait né à Perge autour de 240 av. Apollonius de Perge. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Natif de Perge (Perga, actuelle ville turque proche d'Antalya), Apollonius, également connu sous le nom d'Apollonios de Perga, étudia à Alexandrie et fut un disciple d'Euclide et d'Archimède. Après de nombreuses années à Pergame (Bergama, turquie, proche d'Izmir) où une bibliothèque à l'image de celle d'Alexandrie fut fondée vers 170 avant J. -C., Apollonius s'installa à Alexandrie. Mathématicien, physicien et astronome, on lui doit un traité complet et de très beaux résultats sur les sections coniques (ainsi dénommées par lui), intersections d'un plan et d'un cône, lors de travaux probablement liés à la recherche d'une courbe auxiliaire dans la résolution du célèbre problème de la duplication du cube, autrefois (déjà...) étudié par Ménechme.
Le reste de l'ouvrage nous fut transmis par les mathématiciens arabes. Définition historique des coniques. Ménechme et Appollonius Sources : Encyclopédie Wikipédia : Ménechme (milieu du IVe siècle avant J.C., circa -380 - circa -320) était un mathématicien et géomètre grec. Il est né à Alopeconnesus, de nos jours en Turquie. Coniques. 1B coniques cours et exercices. Coniques. IVe siècle av. J. -C. Ménechme ( -375 à – 325), élève de Platon et précepteur d'Alexandre le Grand, découvre les coniques en tentant de réaliser la duplication du cube.
Un siècle plus tard dans son traité, Apollonius de Perge nommera les trois courbes: parabolé, ellipsis et hyperbolé qui signifient: "jeter à côté" à fin de comparaison, manque et excès. Johannes Werner (1468-1522), prêtre, fabricant d'instruments, adepte d'astrologie, voisin et ami d'Albrecht Dürer. Albrecht Dürer (1471-1528) en quête des secrets de la beauté, cet artiste de la renaissance s'est intéressé à la géométrie des Grecs anciens. 1525 – Instructions pour la mesure, à la règle et au compas, des lignes, plans et corps solides (Ce document passe comme le premier ouvrage important de mathématiques en allemand). LES CONIQUES CELEBRES : PARABOLE, ELLIPSE, HYPERBOLE. Maths Spé. Coniques. 13Coniques. Définition des coniques par foyer et directrice. Nous avons vu ici que dans les points de la parabole peuvent être caractérisés par une propriété métrique mettant en jeu un point et une droite. Hyperbole Trigonométrique. Coniques. Hyberbole.
Calculating with hyperbolas and parabolas tournes 2015. 03 Courbe représentative d'une fonction polynome de degré 2 from MathScope APMEP on Vimeo. 05 Déterminer les coordonnées du sommet d’une parabole à partir de la forme développée. Miroir parabolique du four solaire de 1 mégawatt du site PROMES d'Odeillo-Font Romeu. Mathématiques - le four solaire (une propriété de la parabole)
Espace pédagogique > disciplines du second degré > mathématiques > enseignement > actions nationales > 2019-2021 mis à jour le 09/06/2020 Lorsqu'on désire en faire plus avec des élèves de terminale qui se destinent à des études scientifiques. mots clés : modélisation, parabole Durée 5h réparties sur 5 semaines Le contexte. Antenne parabolique / Études // Études Mathématiques.
Making a Mirror with a Variable Surface Shape. Balistique. Ellipses. Ellipse. Newton. 3.1. Construction du centre de l'ellipse Les tangentes ABG, BCF, GCD, FDE et EA sont données. Maths: L'ellipse. Astrogebra La détermination de l'orbite elliptique de Mars. Astrogebra La détermination de l’orbite elliptique de Mars par Kepler 2010/02/27 L'orbite de Mars par Kepler Principe de la méthode de Kepler • Pour un objet inaccessible, la méthode des parallaxes, qui consiste le viser à partir de deux sites différents, permet de déterminer la distance qui le sépare de l’observateur. • Kepler a utilisé cette méthode pour situer Mars par rapport à la Terre, la planète étant beaucoup plus près de nous que le fond du ciel avec les étoiles constituant le décor. • Cependant la distance de Mars à la Terre est telle que, même en se plaçant en deux points diamétralement opposés de la Terre, on ne pourrait voir Mars sous deux angles sensiblement différents.
Au temps t 1 2010/02/27 L'orbite de Mars par Kepler 4 Au temps t 2 = T 1 + 1 période de Mars est revenu à la même place et la Terre a fait un tour de plus 2010/02/27 L'orbite de Mars par Kepler 5. Affinites et ellipses 2012. Ellipses and Elliptic Orbits. La dualité. Mesdames et messieurs. Blaise Pascal. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Philosophe de renom, auteur des célèbres Pensées, mathématicien et physicien. Sa mère mourut alors qu'il n'avait que 3ans; il fut élevé et instruit par son père Étienne Pascal, comptable et mathématicien reconnu (1588-1651) de l'époque (celle de Mersenne), à qui l'on doit l'étude du limaçon portant son nom, en fait une conchoïde de cercle. Le théorème de Pascal. Théorème sur la colinéarité de trois points générés à partir d'un hexagone inscrit sur une conique.
A 16 Year Old Discovered This AMAZING Geometry Hidden Pattern. Pascal's Theorem. Grand théorème de Poncelet. Deux ellipses et un pentagone variable En géométrie, le grand théorème de Poncelet (parfois appelé porisme de Poncelet), du nom du mathématicien français Jean-Victor Poncelet, est un énoncé portant sur l'inscription des polygones dans les coniques. Il est, selon Marcel Berger, « de loin, le plus beau résultat sur les coniques »[1]. Théorème de Brianchon. Ceci s'applique à toute conique en particulier une paire de droites (théorème de Pappus). Il suffit de le démontrer pour un cercle, et de transformer la figure par projection centrale.
Appliquons le théorème de Menelaüs au triangle GHI avec les transversales : DVC, AUB et EWF. DVC : VH/VI · CI/CG · DG/DH = 1 AUB : AH/AI . Polygones inscrits dans une ellipse, maximisant aire ou périmètre. Lattice points on ellipses. Ellipsographe. Un ellipsoïde peut en cacher un autre. Ellipsoïde. Qu’il s’agisse de missions d’observation de la Terre, de ses océans, de son champ magnétique ou de télécommunications, l’utilisation de satellites en orbite autour de notre planète est devenue banale.
3 J.J. DAHAN ATCM 2020. (1) 4 J.J. DAHAN ATCM 2020. 5 J.J. DAHAN ATCM 2020. (1) 6 J.J. DAHAN ATCM 2020. (1) 7 J.J. DAHAN ATCM 2020. Modeles de Beltrami. Quadriques. Coniques Quadriques. Quadriques. La forteresse de Boukhara, l'hyperboloïde et le paraboloïde, par Hervé Lehning. Inversion conique. Ellipsoïde. Ellipsoïde de révolution. Construire votre ellipsoïde en accordéon. Ellipse sphérique. Paraboloïde de révolution. Paraboloïde hyperbolique. Pringles : modélisation (paraboloïde hyperbolique)
Tous les patrons. Paraboloïde elliptique. Hyperboloïde à une nappe. Hyperboloïde à 2 nappes. Hyperboloïde à 1 ou 2 nappes ? Alexander Veselov: Geodesic scattering on hyperboloids. Hélice du H1. Hélice elliptique. Hélice du paraboloïde. Transformation par polaires réciproques. Famille à un paramètre de coniques utilisant des courbes de Bézier à poids complexes Becar Fuchs Garnier. Quadriques conformes geometry3.