

Bd logique. Z. Mesnil - Logique et apprentissage du langage et du raisonnement mathématiques. Notions de logique. Exercices corrigés de logique. 3 cours & 98 sujets de mathématiques pour les ingénieurs en informatiques. LE DÉMINEUR ET LA LOGIQUE, RÉDUCTION ET ÉQUIVALENCE. J’ai souvent entendu la blague suivante quand j’apprenais à programmer.
Vous donnez à un robot [1] un paquet de pâtes, une casserole, une plaque chauffante, et un robinet d’eau. Puis vous lui apprenez comment faire des pâtes. Quelques jours plus tard, vous demandez au robot de faire des pâtes, en lui disant qu’il y a de l’eau bouillante dans la casserole. Vous voyez alors le robot vider la casserole dans l’évier. Quand vous lui demandez pourquoi, il vous répond que, pour faire des pâtes, on lui a dit qu’il fallait commencer avec une casserole vide.
Une introduction à la notion de réduction Intuitivement, effectuer une réduction signifie que, à partir de la première situation, vous pouvez atteindre la seconde facilement. Quantificateurs. Logiques et raisonnements partie 1 : Introduction. Logiques et raisonnements partie 2 : Assertion. 3 ntsLogique. 4 ntsAideMem1. 2 ntsRevision. 6 ntsRelations. 7 ntsInfinis. 8 ntsRecurr. 5 ntsAideMem2. 3 ntsLogique. Logique.
Implication. Relations. Construire des portes logiques avec des dominos. Logique et ensembles exercice 1. Logique Binaire. Lois de De Morgan. Un article de Wikipédia, l'encyclopédie libre.
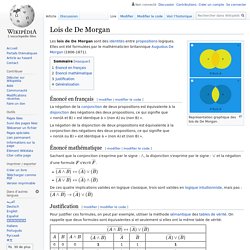
Représentation graphique des lois de De Morgan. Énoncé en français[modifier | modifier le code] Podcast Logique Mathématique et informatique théorique Maison Poincaré. 1MRe Notion elem. 400. Théorème confi(n)ant des Goguettes (en trio mais à quatre) Cours Raisonnements, Ensembles, Applications. Cours maths sup, prépa HEC, BCPST. La négation logique (sans maths) Quart d'Heure Insolite : induction et falsification. Logique. Assertions. Ensembles. Logique (suite). Assertions. Connecteurs logiques. Quantificateurs. LOI DE DE MORGAN. DÉMONSTRATION BTS SIO.
L'histoire de George Boole ou presque... Algèbre de Boole (tables de vérité) Logique (suite). Raisonnements. Découverte Junior Gérard Villemin Logique des ascenseurs. Découverte Junior Gérard Villemin Ascenseur Circuit logique. ALGÈBRE DE BOOLE. PROPRIÉTÉS. Introduction à l'algèbre booléenne. MATHEMATIQUES DISCRETES Chapitre 9 François Meunier DMI Algèbre.
MATHÉMATIQUES DISCRÈTES Chapitre 9 François Meunier DMI Algèbre Booléenne ?

L Une généralisation mineure de la logique propositionnelle. l l En général, l’algèbre est une structure mathématique satisfaisant certains axiomes algébriques standards. Généralise les règles de logiques propositionnelles sur des ensembles autres que {T, F}. l Ex. , sur l’ensemble {0, 1} de bits en base-2, ou l’ensemble {VL, VH} des niveaux de voltage bas et haut d’un circuit. Offre les opérations et les règles pour traiter les ensembles {0, 1} l Cette forme d’algèbre peut être utilisée pour le design des circuits logiques digitaux. l.
Unit 4 Logique combinatoire Objectifs la fin de. Unité 4: Logique combinatoire Objectifs : À la fin de cette unité, vous comprendrez le fonctionnement des principaux éléments d'un ordinateur : décaleur, additionneur, unité logique et arithmétique.
Pour y arriver, vous devrez avoir atteint les objectifs suivants : - décrire le fonctionnement et les propriétés des portes logiques, de circuits combinatoires simples tels que le décodeur, le multiplexeur et le démultiplexeur; - utiliser les théorèmes et les identités de l'algèbre de Boole pour synthétiser un circuit à partir de sa table de vérité et simplifier le résultat obtenu. ©Pierre Marchand, 2001 111 Digital Works Pour mieux profiter des unités 4 à 6, nous vous encourageons à utiliser le logiciel Digital Works, disponible gratuitement à l’adresse : http: //www. mecanique. co. uk/digital-works/ Le logiciel est également disponible dans les laboratoires 3910 et 3966. Comment les ordinateurs calculent-ils ? La logique d'Aristote. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Outre la notion de syllogisme, on doit à Aristote les acceptions actuelles du vocabulaire (cadre jaune) lié au raisonnement déductif (on parle aussi de raisonnement hypothético-déductif), exposées dans les Topiques et dans ses traités sur la logique, Les Analytiques, La métaphysique : C'est chez Aristote que l'on trouve pour la première fois un langage propositionnel du type : si P alors Q.

Lois de Morgan. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Si A et B sont deux propositions susceptibles d'être vraies ou fausses, notons nonA (resp. nonB) la négation de A (resp. de B).

On nomme lois de Morgan, les deux lois usuelles de logique propositionnelle : non (A ou B) = (nonA) et (nonB) nier A ou B, c'est nier A et nier B (ni A ni B) dire que x = ±1 est faux c'est dire x ≠ 1 et x ≠ -1 non (A et B) = (nonA) ou (nonB) nier la coexistence de A et de B, c'est nier A ou nier B dire que x est divisible par 2 et par 3 est faux, c'est dire que x est non divisible par 2 ou que x est non divisible par 3 i Les égalités "logiques"ci-dessus, utilisées par ailleurs dans cette page sont en fait des équivalences logiques : au lieu de « égale » on conviendra de lire « revient à dire ». EMF2012GT3MESNIL. Logique. Enseignements en logique Lyon. Introduction à la logique mathématique. Polycopié première partie.
(Notes des années précédentes susceptibles d'être modifiées.)TD : fiche 1, fiche 2, fiche 3. Les notes du cours Logique et théorie des ensembles de Patrick Dehornoy fournissent une bonne ressource bibliographique pour cette partie. Autre référence bibliographique : Jean-Louis Krivine, Théorie des ensemble, Cassini 2007. Poly logique. Logique et langage des ensembles-Logique et langage des ensembles. 1. Logique mathématique (Bac+1) Calculi, petits cailloux et mathématiques - Petits riens de mathématiques, de logique et de leurs histoires, pour tous. Introduction à la logique mathématique. Nous avons maintenant tous les outils en main pour réaliser des raisonnements mathématiques complets.
Un raisonnement permet d'établir une proposition à partir d'une ou de plusieurs propositions initiales admises (ou précédemment démontrées) en suivant les règles de la logique. Nous allons dans cette dernière partie détailler quatre "types" de raisonnement, quatre "méthodes" pour démontrer une proposition : Trouver un exemple ou un contre-exempleDémontrer la contraposéeRaisonner par l'absurdeRaisonner par récurrence Ces différentes formes de raisonnements devront s'appliquer dans des cas bien particuliers.
Logique. Logigrilles Enigme d'Einstein Combinatoire. Inspecteur Logic. Activite connecteurs groupe logique. Logique et raisonnements - partie 1 : logique. La barre de Sheffer - E. Duyckaerts. Introduction à l'algèbre booléenne. Le tableau de Karnaugh. Exercices logique raisonnement. La négation logique (sans maths) Logique avec Python. Qu’est-ce qu’un booléen ?
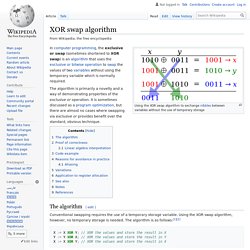
Voir la page sur Wikipédia C’est une variable qui ne peux prendre que deux valeurs : VRAI ou FAUX.En Python, le type d’une telle variable est bool, les deux valeurs possibles sont True ou False. Expressions booléennes. XOR swap algorithm. Using the XOR swap algorithm to exchange nibbles between variables without the use of temporary storage The algorithm is primarily a novelty and a way of demonstrating properties of the exclusive or operation.
Slides groupe seminaire. La logique et ses paradoxes. La logique et ses paradoxes Yves SAGNIER La logique est pour certains le soubassement indispensable des mathématiques dont elle fait partie, pour d'autres, ce sont les mathématiques qui sont un sous-ensemble de la logique. En tout cas, au cours de l'histoire des mathématiques, les deux ont toujours été étroitement liées. On parle parfois de « logique euclidienne » alors qu'Euclide ne s'est occupé que de géométrie. Paradoxes mathématiques. Les chroniques suivantes ont pour thèmes les paradoxes mathématiques. Elles illustraient les programmes d'interrogations de l'année 2002-2003. Les paradoxes sémantiques Les paradoxes de logique mathématique et de théorie des ensembles Les paradoxes sur la notion d'infini Les paradoxes de la théorie de la mesure.
Paradoxe ou sophisme ? On confond souvent les paradoxes et les sophismes, au point de mettre le mot « paradoxe » à toutes les sauces, même quand c'est un abus de langage. Alors quelle est la différence et quelles sont les utilités de ces raisonnements ? Le paradoxe est un raisonnement juste mais qui conduit à une contradiction. Par contradiction, on entend soit qu'il conduit à deux conclusions opposées, soit qu'il amène à une conclusion contredisant les principes auparavant établis.
Le sophisme conduit également à une contradiction. Cependant, c'est cette fois parce que le raisonnement contient une erreur volontaire et dissimulée. Quelles sont les utilités de ces raisonnements ? Le jeu de logique de Lewis Carroll. La version en ligne. Le rêve de Leibniz ou calculus ratiocinator était de pouvoir traduire n’importe quel problème de logique dans un langage parfait (la caractéristique universelle) manipuler des symboles dans ce langage (soit, mener un calcul) pour résoudre le problème de logique.
Or la seconde étape, et même dans une certaine mesure, la première, est mécanique donc a priori abordable par une machine. Eléments de logique mathématique - PPS. Lectureall. Introduction à la logique floue. R7428 [francais] Techniques de l'ingénieur Application de la logique floue Commande de la tem. Test logique (humour) Tables de verite. Cours ould. Les problèmes SAT... et les graphes. Z. Mesnil - Logique et apprentissage du langage et du raisonnement mathématiques - PeerTube. Zoé Mesnil - La logique : d'un outil pour le langage et le raisonnement mathématiques vers un objet d'enseignement - PeerTube. C. Hache et Z. Mesnil - Outils logiques pour analyser les formulations des preuves dans des manuels de lycée - PeerTube.
Zorn.
G. Sabbagh - Une ancienne analogie, généralement (à juste titre ?) négligée… - PeerTube. Comment raisonner sur un logiciel ? La naissance des logiques de programmes - Sciences du logiciel - Xavier Leroy - Collège de France - 04 mars 2021 09:30. Comment s'assurer qu'un logiciel fait ce qu'il est censé faire ? Les méthodes classiques de vérification et de validation du logiciel, reposant sur le test, les revues et les analyses, ne suffisent pas toujours. La vérification déductive permet d'aller plus loin en établissant des propriétés vraies de toutes les exécutions possibles d'un programme, via des raisonnements formels au sein d'une logique appropriée : une logique de programmes.
Le premier cours a illustré cette approche par la vérification déductive d'une fonction de recherche dichotomique dans un tableau trié, un algorithme très utilisé et souvent implémenté de manière incorrecte. Ensuite, le cours a retracé l'émergence de la vérification déductive et des logiques de programmes via trois publications fondatrices. L'article de Robert W. Enfin, l'article de C. Les chemins d'une découverte : la correspondance de Curry-Howard, 1930-1970 - Sciences du logiciel - Xavier Leroy - Collège de France - 21 novembre 2018 10:00. POD - Preuve Par Consistance (L(G) Dans L) 10 Channels. POD - Preuve De Complétude (L Dans L(G)) POD - Validité De La Preuve Par Induction Nœthér... 10 Channels International126 videos La formation336 videos Orientation and Professional Integration69 videos Pédagogies innovantes248 videos Presse83 videos Research2376 videos Ressources humaines35 videos Student life6 videos Tutorials103 videos University63 videos Types of videos.
Portail:Logique. Logique classique. Un article de Wikipédia, l'encyclopédie libre. Déduction logique. Une déduction logique est définie de manière à être à la fois nécessaire et formelle et est explicitée dans des domaines comme la théorie des modèles, qui permet de trouver des univers mathématiques dans lesquels la relation est utile et fournit un sens aux formules, et la théorie de la démonstration, qui fournit un cadre théorique pour sa définition de manière syntaxique[1]. Une formule est une conséquence d'un ensemble d'autres formules, dans un langage, si et seulement si, en utilisant la logique elle-même (c'est-à-dire sans chercher à donner un sens aux formules) la formule doit être vraie si toutes les formules de l’ensemble des prémisses sont elles aussi vraies[3]. Déduction naturelle. Tautologie. La tautologie (du grec ancien ταὐτολογία, composé de ταὐτό, « la même chose », et λέγω, « dire » : le fait de redire la même chose) est une phrase ou un effet de style ainsi tourné que sa formulation ne puisse être que vraie.
Modus ponens. Un article de Wikipédia, l'encyclopédie libre. Principe du tiers exclu. En logique formelle, le principe du tiers exclu (ou « principe du milieu exclu » ou « tertium non datur » ou «principium medii exclusï[Quoi ?] »[1], ou simplement le « tiers exclu ») énonce qu'ou bien une proposition est vraie, ou bien sa négation est vraie. Raisonnement par l'absurde. Système à la Hilbert. Liste des paradoxes — Wikipédia.