

Mot-clé - Vision artificielle et traitement d’images. Modèles n-grammes et n-classes pour la reconnaissance de l'écriture manuscrite en ligne : Modélisation probabiliste du langage naturel = N-gram and n-class models for on-line handwriting recognition : Probabilistic language modelling. Titre du document / Document title Auteur(s) / Author(s) Affiliation(s) du ou des auteurs / Author(s) Affiliation(s) (1) Société Vision Objects - 9, rue du Pavillon, 44980 Sainte Luce sur Loire, FRANCE(2) Institut de Recherche en Informatique de Nantes, 2, rue de la Houssinière - BP 92208, 44322 Nantes, FRANCE(3) Institut de Recherche en Communications et Cybernétique de Nantes UMR CNRS, La Chantrerie - Rue Christian Panc - BP 50609, 44306 Nantes, FRANCE Résumé / Abstract Dans ce travail, nous étudions l'apport d'un modèle de langage pour améliorer les performances des systèmes de reconnaissance de l'écriture manuscrite en ligne.

Revue / Journal Title Source / Source 2003, vol. 44, no1, pp. 63-92 [30 page(s) (article)] (1 p.3/4) Langue / Language Français Revue : Anglais Editeur / Publisher. Combien d’objets dans une image ? - INRIA. Traitement d’images pour l’évaluation des ressources forestières. Les nouvelles données images très haute résolution peuvent beaucoup apporter aux inventaires forestiers, puisqu'elles fournissent de l'information à l'échelle de l'arbre.
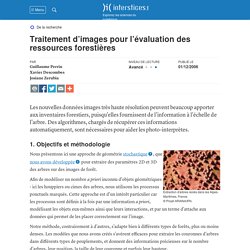
Des algorithmes, chargés de récupérer ces informations automatiquement, sont nécessaires pour aider les photo-interprètes. 1. Objectifs et méthodologie Afin de modéliser un nombre a priori inconnu d'objets géométriques - ici les houppiers ou cimes des arbres, nous utilisons les processus ponctuels marqués. Cette approche est d'un intérêt particulier car les processus sont définis à la fois par une information a priori, modélisant les objets eux-mêmes ainsi que leurs interactions, et par un terme d'attache aux données qui permet de les placer correctement sur l'image.
Notre méthode, contrairement à d'autres, s'adapte bien à différents types de forêts, plus ou moins denses. Ainsi, des statistiques sur le nombre d'arbres, leur taille ou la densité de la parcelle peuvent être obtenues. Les forêts de France et leur inventaire. Images des mathématiques. Images numériques et compressions Une image numérique, telle qu’on peut la voir sur un écran d’ordinateur, est une mosaïque de pixels (picture elements) dont la couleur est choisie dans un ensemble fini : il s’agit d’un objet naturellement discret.

Il s’identifie à une matrice à h colonnes et v lignes dont les éléments appartiennent à un ensemble finiE. Typiquement, pour une image en niveau de gris, E est constitué des entiers compris entre 0 et 255 et correspond à l’intensité lumineuse de chaque pixel. Ces 256 valeurs distinctes se codent avec 8 bits (2^8=256), d’où le nom d’image 8 bits. Pour les images couleurs, chaque pixel est caractérisé par 3 intensités lumineuses, celles des canaux rouge, vert et bleu, définissant des images 3\times8=24 bits. Le stockage en mémoire d’une image couleur requiert donc h\times v\times24 bits. Figure 1. Compression sans perte L’entropie de Shannon telle que si un codage est possible en \bar n bits en moyenne alors nécessairement \bar n \geq H(X)\quad. Morphologie mathématique. Une forme (en bleu), sa dilatation morphologique (en vert), et son érosion morphologique (en jaune) par un élément structurant en forme de diamant.
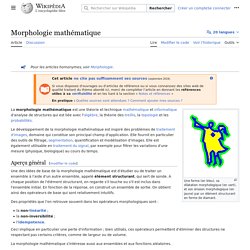
Le développement de la morphologie mathématique est inspiré des problèmes de traitement d'images, domaine qui constitue son principal champ d'application. Elle fournit en particulier des outils de filtrage, segmentation, quantification et modélisation d'images. Elle est également utilisable en traitement du signal, par exemple pour filtrer les variations d'une mesure (physique, biologique) au cours du temps. Aperçu général[modifier | modifier le code] Une des idées de base de la morphologie mathématique est d'étudier ou de traiter un ensemble à l'aide d'un autre ensemble, appelé élément structurant, qui sert de sonde.
Des propriétés que l'on retrouve souvent dans les opérateurs morphologiques sont : la non-linéarité ;la non-inversibilité ;l'idempotence. La morphologie mathématique s'intéresse aussi aux ensembles et aux fonctions aléatoires.