

Mathematician announces that he's proved the ABC conjecture. (Phys.org)—In all of history there are very few names that stand out in the field of mathematics, at least among those not in the field: Euclid, Newton, Pythagoras, etc.

This is likely due to several reasons, chief among them is that math is so seldom used by most people and the fact that its use in other sciences causes the underlying concepts to become overshadowed. That might change if what Shinichi Mochizuki of Kyoto University is claiming is true; that he has written a proof of the ABC conjecture. To mathematicians it's akin to the Grand Unified Theory of physics, a proof that would tie together most of the fundamental ideas in the field into one neat, fully explainable bundle. The ABC conjecture is at its core, an association between whole numbers and is formed on the basis of the simple mathematical equation a+b=c and involves what are known as square free numbers; numbers that can't be divided by a number squared.
Explore further: Pseudo-mathematics and financial charlatanism. Proof Claimed for Deep Connection between Prime Numbers. From Nature magazine The usually quiet world of mathematics is abuzz with a claim that one of the most important problems in number theory has been solved.
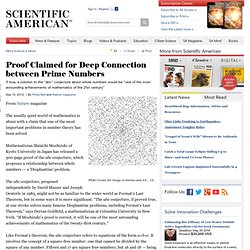
Mathematician Shinichi Mochizuki of Kyoto University in Japan has released a 500-page proof of the abc conjecture, which proposes a relationship between whole numbers — a 'Diophantine' problem. The abc conjecture, proposed independently by David Masser and Joseph Oesterle in 1985, might not be as familiar to the wider world as Fermat’s Last Theorem, but in some ways it is more significant. “The abc conjecture, if proved true, at one stroke solves many famous Diophantine problems, including Fermat's Last Theorem,” says Dorian Goldfeld, a mathematician at Columbia University in New York. Mathematician Claims Proof of Connection between Prime Numbers. A Japanese mathematician claims to have the proof for the ABC conjecture, a statement about the relationship between prime numbers that has been called the most important unsolved problem in number theory.
If Shinichi Mochizuki's 500-page proof stands up to scrutiny, mathematicians say it will represent one of the most astounding achievements of mathematics of the twenty-first century. The proof will also have ramifications all over mathematics, and even in the real-world field of data encryption. The ABC conjecture, proposed independently by the mathematicians David Masser and Joseph Oesterle in 1985 but not proven by them, involves the concept of square-free numbers, or numbers that cannot be divided by the square of any number.
(A square number is the product of some integer with itself). The ABC conjecture makes a statement about pairs of numbers that have no prime factors in common, Peterson explained. And now, one such climber may have reached the summit. What is the abc conjecture? What is the abc conjecture | Open and solved problems | Consequences | The algorithm Abc triples The abc conjecture is about abc triples. abc triples are triples of numbers with some special properties.
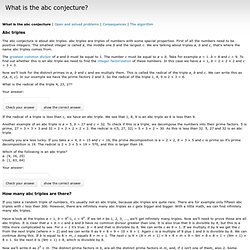
First of all the numbers need to be positive integers. The smallest integer is called a, the middle one b and the largest c. We are talking about triples a, b and c, that's where the name abc triples comes from. The greatest common divisor of a and b must be equal to 1. Now we'll look for the distinct primes in a, b and c and we multiply them. Abc conjecture. Abc Conjecture. Proof of the abc Conjecture? Jordan Ellenberg at Quomodocumque reports here on a potential breakthrough in number theory, a claimed proof of the abc conjecture by Shin Mochizuki.

More than five years ago I wrote a posting with the same title, reporting on a talk by Lucien Szpiro claiming a proof of this conjecture (the proof soon was found to have a flaw). One change over the last five years is that now there are excellent Wikipedia articles about mathematically important questions like this conjecture, so you should consult the Wikipedia article for more details on the mathematics of the conjecture. To get some idea of the significance of this, that article quotes my colleague and next-door office neighbor Dorian Goldfeld describing the conjecture as “the most important unsolved problem in Diophantine analysis”, i.e. for a very significant part of number theory.
What experts tell me is that, very much unlike the case of Szpiro’s proof, here it may take a very long time to see if this is really a proof. Proof claimed for deep connection between primes. The usually quiet world of mathematics is abuzz with a claim that one of the most important problems in number theory has been solved.

Mathematician Shinichi Mochizuki of Kyoto University in Japan has released a 500-page proof of the abc conjecture, which proposes a relationship between whole numbers — a 'Diophantine' problem. The abc conjecture, proposed independently by David Masser and Joseph Oesterle in 1985, might not be as familiar to the wider world as Fermat’s Last Theorem, but in some ways it is more significant. “The abc conjecture, if proved true, at one stroke solves many famous Diophantine problems, including Fermat's Last Theorem,” says Dorian Goldfeld, a mathematician at Columbia University in New York.