

Patricia tree insertion. Visualizing range trees. Range trees are a data structure which lets you efficiently query a set of points and figure out what points are in some bounding box.

They do so by maintaining nested trees: the first level is sorted on the x-coordinate, the second level on the y-coordinate, and so forth. Unfortunately, due to their fractal nature, range trees a bit hard to visualize. 13.1 BinaryTrie: A digital search tree. A BinaryTrie encodes a set of bit integers in a binary tree.

All leaves in the tree have depth and each integer is encoded as a root-to-leaf path. The path for the integer turns left at level if the th most significant bit of. B-Trees. Data Structures and Algorithms with Object-Oriented Design Patterns in Java Just as AVL trees are balanced binary search trees, B-trees are balanced M-way search trees.

By imposing a balance condition , the shape of an AVL tree is constrained in a way which guarantees that the search, insertion, and withdrawal operations are all , where n is the number of items in the tree. Suffix. Have You Seen This String?

The Suffix TreeLet's Find That SubstringOther Nifty Things You Can Do with a Suffix TreeHow to Build Your Very Own Suffix TreeExercisesReferences and Selected Readings Have You Seen This String? Hash table - CS Animated. Kruse_Chapter_10_Binary_Trees.pdf (application/pdf Object) Splay Trees. Summary Splay Trees were invented by Sleator and Tarjan.

This data structure is essentially a binary tree with special update and access rules. It has the wonderful property to adapt optimally to a sequence of tree operations. More precisely, a sequence of m operations on a tree with initially n nodes takes time O (n ln (n) + m ln (n)). Operations Splay trees support the following operations. Each split, join, delete and insert operation can be reduced to splay operations and modifications of the tree at the root which take only constant time. Splay Tree Demo. 13.1-7 Describe A Red-black Tree On N Keys That... Can I Have Solution For This Problem 13.1-7... Trees1.pdf (application/pdf Object) B-tree algorithms. A B-tree is a data structure that maintains an ordered set of data and allows efficient operations to find, delete, insert, and browse the data.

Binary Trees. Introduction More tree terminology: The depth of a node is the number of edges from the root to the node.The height of a node is the number of edges from the node to the deepest leaf.

The height of a tree is a height of the root. AAW. The main motivation behind this site is as a teaching aid in the field of algorithms and data-structures.

A series of applets, including algorithm pseudocode, are provided to illustrate the workings of important algorithms in Computer Science. Hashing (by Hang Thi Anh Pham, 2001) Splay Tree (by Sotirios Stergiopoulos, 2001) Red Black Tree (by Sotirios Stergiopoulos, 2001) PRIORITY QUEUES:Leftist and Skew Heaps (by Soheil Pourhashemi, 2007) Binomial Heap (by Sotirios Stergiopoulos, 2001) Fibonacci Heap (by Jason Huang Hu & Wei Wang, 2003) DYNAMIC PROGRAMMING:Optimal Static Binary Search Tree (by Roman Gubarenko, 2005) Dijkstra - Single Source Shortest Paths (by Hai Feng Huang, 2005) Minimum Spanning Tree (by Dena Ghiassi, 2005) Max-Flow Min-Cut (by Hai Feng Huang, 2006. B-Trees. Simple B-Tree Implementation in Java. Tracing Find Algorithm for BTree. Consider the following tree: If we were to search for the node 100, we would do the following: 1. check 100 vs 29, clearly larger, on to next key 2. but there is no key, so go to last child 3. check 100 vs 37, clearly larger, on to next key 4. check 100 vs 50, clearly larger, on to next key 5. there is no key, so go to last child 6. check 100 vs 50 (in the leaf now), larger, on to next key 7. check 100 vs 100, success!
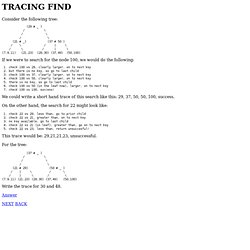
We could write a short hand trace of this search like this: 29, 37, 50, 50, 100, success. Binary Trees. By Nick Parlante This article introduces the basic concepts of binary trees, and then works through a series of practice problems with solution code in C/C++ and Java.

Binary trees have an elegant recursive pointer structure, so they are a good way to learn recursive pointer algorithms. Contents Section 1. Binary Tree Structure -- a quick introduction to binary trees and the code that operates on them Section 2. Stanford CS Education Library -- #110 This is article #110 in the Stanford CS Education Library. Related CSLibrary Articles. Computer Algorithms: Heap and Heapsort. Introduction Heapsort is one of the general sorting algorithms that performs in O(n.log(n)) in the worst-case, just like merge sort and quicksort, but sorts in place – as quicksort. Although quicksort’s worst-case sorting time is O(n2) it’s often considered that it beats other sorting algorithms in practice. Thus in practice quicksort is “faster” than heapsort. In the same time developers tend to consider heapsort as more difficult to implement than other n.log(n) sorting algorithms. Heaps. Data Structures/Min and Max Heaps.
A heap is an efficient semi-ordered data structure for storing a collection of orderable data. A min-heap supports two operations: INSERT(heap, element) element REMOVE_MIN(heap) (we discuss min-heaps, but there's no real difference between min and max heaps, except how the comparison is interpreted.) This chapter will refer exclusively to binary heaps, although different types of heaps exist. The term binary heap and heap are interchangeable in most cases. Heap (data structure) Example of a complete binary max-heap with node keys being integers from 1 to 100 1. the min-heap property: the value of each node is greater than or equal to the value of its parent, with the minimum-value element at the root. 2. the max-heap property: the value of each node is less than or equal to the value of its parent, with the maximum-value element at the root.
Throughout this article the word heap will always refer to a min-heap. In a heap the highest (or lowest) priority element is always stored at the root, hence the name heap. A heap is not a sorted structure and can be regarded as partially ordered. Note that, as shown in the graphic, there is no implied ordering between siblings or cousins and no implied sequence for an in-order traversal (as there would be in, e.g., a binary search tree).
Min heap and max heap. Build Heap. Build-Max-Heap "Max" refers to the fact that this algorithm calls Max-Heapify, which guarantees that the object the with the largest value is at the top of the heap. Helper function definitions used by Max-Heapify. Priority queue. Double-ended queue. Naming conventions[edit] Distinctions and sub-types[edit] This differs from the queue abstract data type or First-In-First-Out List (FIFO), where elements can only be added to one end and removed from the other. Queue (abstract data type)