

Accueil – mois en cours – M@ths + Numération - Opérations. Numération - Opérations. Boulier. Dans MHM maternelle, on propose de travailler avec ce boulier simple, ou ensuite avec des bouliers avec deux branches.
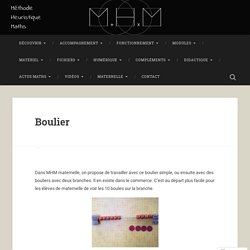
Il en existe dans le commerce. C’est au départ plus facile pour les élèves de maternelle de voir les 10 boules sur la branche. Ce matériel peut être fabriqué avec les élèves, en utilisant des porte-manteaux. En classe, ils pourront d’abord être présentés à l’accueil ou en regroupement. Présentation de boulier maison à une tige ,boulier éphémère au tableau et un boulier traditionnel. Le boulier est très riche et permet de réaliser un travail important sur les nombres, leurs décomposition, leur construction, etc. Exemples : associer les manipulations de petits bonhommes à l’utilisation du boulier pour commencer à aborder les plus grands nombres en GS. En vidéo : Version numérique: Le site @ClassedeFlorent proposer plusieurs mini applications en ligne autour du boulier parfaitement adaptées ! WordPress: J'aime chargement… Résolution de problèmes en cycle 2. De représenter à modéliser.
Jeux d'images J'avais, en avril, écrit une séance à partir de l'ouvrage Jeux d'images édité chez Circonflexe, que je trouve tout à fait excellent pour travailler la compétence représenter, de façon transversale, dans le domaine de la verbalisation et pour consolider aussi la compétence représenter en mathématiques.

C'est dans cet article. Et… Dans "A l'attaque ! " Modéliser ou raisonner ? Une collègue m'a posé ce matin une question intéressante : Lorsqu'un élève reconnait qu'il faut utiliser un théorème (allez, Pythagore pour être encore plus concret) et l'utilise, tu évalues quelle compétence? Présentation de la RESSOURCE - 10 PROBLEMES PAR SEMAINE - PeerTube Temporaire COVID-19- academie de Grenoble. Modèle en barre manipulation - PeerTube Temporaire COVID-19- academie de Grenoble. Un nouveau regard sur la résolution de problèmes - Espace pédagogique. Résoudre des problèmes à l’aide du modèle en barres Image2 Le modèle en barre est un modèle ancien qui existait dans l’enseignement français avant la réforme des maths moderne.

Mathématiques : du concret vers l'abstrait - Pass Education. Selon Maria Montessori, l’esprit des mathématiques fait parti de l’esprit absorbant de l’enfant, cette capacité d’abstraire, de raisonner, de chercher, d’imaginer, de calculer, de mesurer et de faire preuve de précision.
Il semblerait que dans la mesure où l’environnement de l’enfant est propice, il a le pouvoir de développer son potentiel mathématique. Maria Montessori parle de périodes sensibles, celle des maths commence vers l’âge de 3 ans et demi jusqu’aux 6 ans de l’enfant. On connaît davantage l’expression « La bosse des maths » et il s’avère que nous en sommes tous dotés ! Oui, nous l’avons tous et c’est vérifiable aujourd’hui grâce à l’imagerie cérébrale.
Edouard Séguin et Maria Montessori en étaient persuadés sans pour autant en apporter la preuve scientifique. Mathématiques en Éducation prioritaire, des ressources pour la formation. Mettre les élèves au travail en résolution de problèmes (arithmétiques) Cycle 2 et 3. Questionner les pratiques ordinaires en résolution de problèmes en mathématiquesInterroger les conditions qui font de la résolution de problèmes une activité utile pour les apprentissages des élèves et une pratique acceptable et réalisable pour les enseignants Format : Deux journées en présentiel et du temps intersession Proposition de Déroulement En amont de la première journée : RAMENER DES TRACES DU RéEL pour poser ensemble le problème et constater les difficultés Proposer à distance, deux semaines avant la session en présentiel un questionnaire (voir encadré ci-contre) aux enseignants pour faire un état des lieux de ce qu’ils font et de leurs préoccupations.

Ce questionnaire en amont peut constituer un passage à risque pour le formateur (risque que les enseignants ne répondent pas). Rencontrer les enseignants dans les écoles en amontTravailler avec le coordonnateur du REPTravailler avec les pilotes du réseau, les directeurs d'écoles. Usages des doigts et enseignement explicite. Mettre au centre la résolution de problèmes. Pourquoi et comment enseigner le nombre à l’école maternelle ?
À cette question, la réponse la plus courante est qu’il faut manipuler. Le sens du nombre et du problème passe au second plan. Et pourtant, est-il si transparent que certains l’imaginent ? La manipulation semble s’imposer comme méthode naturelle d’apprentissage du nombre la plus compatible avec l’âge et le développement des enfants. Pourtant, peut-on envisager l’apprentissage du nombre, concept abstrait, construction de l’esprit humain, en restant dans le registre de la manipulation d’objets matériels ? Penser le monde avant d’agir sur lui Commençons par le pourquoi, si on ne veut pas s’arrêter aux seules raisons du type « c’est au programme ». Il permet de penser le monde avant d’agir sur lui ; il donne la possibilité de renoncer à certaines actions, après en avoir anticipé les conséquences. Dès lors, enfermer son apprentissage dans certaines formes de manipulation peut s’avérer un obstacle à son accès.
MANIPULER EN MATHS. La construction du nombre au cycle 1. Dans cette conférence, Rémi Brissiaud réaffirme l'importance d'enseigner le comptage-dénombrement pour permettre aux élèves de construire le concept de nombre.
Il présente également un outil numérique qui permet cet enseignement : "Les Noums". player1 1- évolution des performances en calcul des élèves de CM2: l'analyse de Rémi Brissiaud En 2017, la reprise d’une enquêteNote d'information de la DEPP N°19.08, Mars 2019 initiée en 1987, portant sur le calcul en fin de CM2, permet de comparer les performances des élèves à trente ans d’intervalle. Cette enquête donne des résultats à quatre temps de mesure : 1987, 1999, 2007 et 2017. Dans La psychologie de l'enfant, 1966, Jean Piaget propose une théorie du développement de l'intelligence chez l'enfant. Les théories piagétiennes, notamment le modèle de l'escalier, sont remises en cause aujourd'hui. Le champs additif et la typologie de Vergnaud – Mon CRPE. Autant vous prévenir d’avance, l’article est long et dense!

Dans la plupart des manuels et des autres fiches que j’ai pu trouvé lorsque j’ai passé le concours, on ne parlait que de la théorie de Vergnaud. Mais je vous avoue m’être questionnée quel est le lien entre la classification des problèmes additifs et soustractifs de Vergnaud et le principe additif ou soustractif? Mais tout d’abord un petit rappel des programmes: Les quatre opérations (addition, soustraction, multiplication, division) sont étudiées à partir de problèmes qui contribuent à leur donner du sens, en particulier des problèmes portant sur des grandeurs ou sur leurs mesures. Manipulation en mathématiques. Manipulation, nombres décimaux aux cycles 1, 2 et 3. Changer la classe pour changer l'école.