

On lui connait deux ouvrages majeurs : le Brāhmasphuṭasiddhānta (ब्राह्मस्फुटसिद्धान्त) en 628 et le Khandakhâdyaka en 665. Brahmagupta. Brahmagupta (ब्रह्मगुप्त) (Multân, 598–670) est un mathématicien et astronome indien.
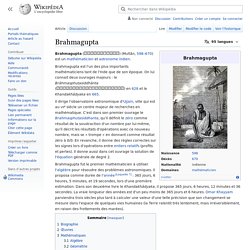
Brahmagupta est l'un des plus importants mathématiciens tant de l'Inde que de son époque. On lui connait deux ouvrages majeurs : le Brāhmasphuṭasiddhānta (ब्राह्मस्फुटसिद्धान्त) en 628 et le Khandakhâdyaka en 665. Il dirige l'observatoire astronomique d'Ujjain, ville qui est au VIIe siècle un centre majeur de recherches en mathématique. Brahmasphutasiddhanta. Théorème de Brahmagupta. Et implique En mathématiques, le théorème de Brahmagupta donne une condition nécessaire sur la perpendicularité des diagonales d'un quadrilatère inscriptible dans un cercle.
Merci pour vos mots d'encouragement. Ajoutons maintenant les mises à jour petit à petit. – varipon
Bonjour, C'est bien normal que votre travail passe avant tout. De mon côté non plus il n'y aura que peu de mises à jour le temps que je passe auprès de ma mère. J'ai regardé la dernière vidéo de votre golfeuse, elle est déjà très aboutie. Félicitations et bon courage pour l'achèvement de votre œuvre. – jadotf
Bonjour J'ai entendu que ce mathématicien indien Brahmagupta est une personne spéciale qui a découvert le concept de zéro il y a longtemps. (Je suis occupé en ce moment et il y a peu de mises à jour. En particulier, l'analyse du mécanisme du swing de golf que j'ai commencé est très difficile et me prive d'une grande partie de ma concentration. La mise à jour sera redémarrée au fil du temps. Je m'intéresse aux considérations mathématiques de l'économie, etc.) – varipon
Excellent! J'ignorais ce théorème. Une fois prouvé que AF = FM, on a directement que F est le centre du cercle circonscrit à AMD et donc que AF=FD. En effet, comme le triangle circonscrit au triangle rectangle AMD a pour diamètre [AD], il suffit de montrer que F est le milieu de [AD]. Ce milieu est le point d'intersection de la médiatrice de [AM] et du segment [AD] (théorème des milieux dans le triangle AMD). – jadotf
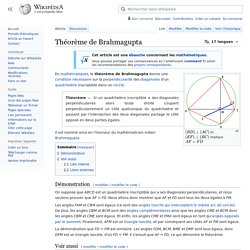
Manuscrit de Bakhshali. Ecriture des chiffres dans le manuscrit de Bakhshali.
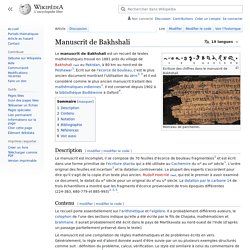
Morceau de parchemin. Le manuscrit de Bakhshali est un recueil de textes mathématiques trouvé en 1881 près du village de Bakhshali (en) au Pakistan, à 80 km au nord-est de Peshawar[1]. Écrit sur de l'écorce de bouleau, c'est le plus ancien document montrant l'utilisation du zéro[2],[3] et il est considéré comme le plus ancien manuscrit traitant des mathématiques indiennes[1].
QUADRILATÈRE : FORMULE DE BRAHMAGUPTA. L'identité de Brahmagupta. Brahmagupta–Fibonacci identity. 217. TS- Bhaskara II et Brahmagupta résolvent une équation de Pell-Fermat. 217. TS Bhaskara II et Brahmagupta résolvent une équation de Pell Fermat. Biographie de Brahmagupta. Brahmagupta est un mathématicien indien du VIIè siècle.

Il vécut une grande partie de sa vie à Bhinmal, sous la protection des souverains de la dynastie des Gurjara. Il dirigea aussi l'observatoire de Ujjain, qui était le principal centre de recherche en mathématiques et en astronomie de l'Inde à cette époque. Il écrivit quatre traités, le plus important étant Brahmasphutasiddhanta, publié en 628 et écrit en vers ce qui lui donne un intérêt poétique. C'est dans l'oeuvre de Brahmagupta que, pour la première fois, le nombre zéro est réellement traité comme un nombre. Brahmagupta donne les règles des opérations utilisant ce nombre, même s'il se trompe en affirmant que 0/0 vaut 0. Brahmagupta. Brahmagupta.