

Les Mathématiques Sont Présentes Dans La Nature [Documentaire Culture] La merveilleuse présence des mathématiques dans la nature. Avez-vous déjà observé la forme d’une fleur de tournesol, la structure d’un flocon de neige ou la morphologie d’une fougère ?
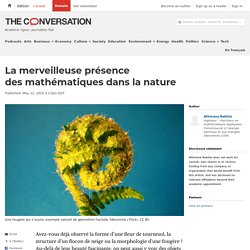
Au-delà de leur beauté fascinante, on peut aussi y voir des objets mathématiques, puisque les spirales de la fleur de tournesol suivent une célèbre suite numérique appelée suite de Fibonacci, les flocons de neige présentent des symétries hexagonales particulières et la morphologie de la fougère décrit une géométrie fractale. De nombreux autres exemples illustrent à quel point les objets mathématiques sont présents dans la nature. Réciproquement, les mathématiques sont utilisées pour comprendre les phénomènes qui nous entourent : c’est par exemple grâce aux équations différentielles que nous pouvons calculer précisément les trajectoires des astres ou prédire le temps qu’il fera dans quelques jours. Les objets mathématiques semblent s’appliquer à presque toutes les sciences avec des performances remarquables.
Mathématiques et biologie L'organisation du vivant Tangente Hors série n° 42 ( PDFDrive ) Maths En Scène / Maths et nature (Partie 1) Maths En Scène / Maths et nature (Partie 2) Maths et biologie 2014. Conscience : L'intelligence du végétal - Reportage offert de l'EXTRA Lab S2E9. Les plantes font-elles des mathématiques ? - CEB T2 2017 - S.Douady - Public Lecture 2. Formes d'art de la nature. Les algorithmes du vivant. Nature et algorithmes. Les algorithmes du vivant. À la pointe des sciences, des technologies et de l’innovation au service de la société, TEDx Saclay, pour sa troisième édition le 30 novembre prochain, a choisi le thème « Au Service du Vivant ».
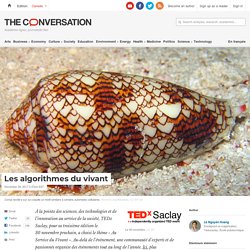
Au-delà de l’évènement, une communauté d’experts et de passionnés organise des évènements tout au long de l’année. Ici, plus d’informations. On a tendance à opposer le monde artificiel et technologique des algorithmes au monde naturel et biologique du vivant. Et pourtant, de nos jours, les algorithmes sont devenus incontournables pour étudier la complexité du vivant.
D’où l’importance croissante des outils informatiques, exacerbée par la prolifération des données : témoin, le séquençage des génomes. De la nature à l’informatique. Algorithmes - Claire Mathieu. [Conférence SML] Des probabilités pour le vivant - Vincent Bansaye. LE HASARD & LA COMPLEXITÉ DES LOGIQUES DU VIVANT. Toile daraignee orsay alainfournier 2016. Que peuvent nous apprendre les flocons de neige sur les mathématiques ? Hélice conique. HÉLICE CONIQUEConical helix (or concho-spiral), konische Böschungslinie L'hélice conique peut être définie comme une hélice tracée sur un cône de révolution (i.e. une courbe faisant un angle constant avec l’axe du cône), ou une loxodromie de ce cône (c'est-à-dire courbe faisant un angle constant avec les méridiennes) ; ce n'est pas une géodésique du cône.Concrètement, on obtient donc une hélice conique lorsque l'on trace un chemin de pente constante sur un cône placé verticalement.
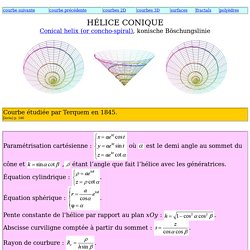
La projection sur xOy est une spirale logarithmique ( ) qui est aussi le lieu des sections des tangentes avec xOy ; la courbe obtenue par développement du cône en est aussi une spirale logarithmique.Comme pour toute hélice, c'est une géodésique du cylindre vertical construit sur la spirale projection sur xOy.La normale principale est constamment perpendiculaire à Oy.Les rayons de courbure et de torsion sont proportionnels à z .L’hélice est dextre lorsque (elle “monte” dans le sens trigonométrique). 65 La coquille des mollusques.
Résumé : Parmi les formes de la vie et les forces qui les modèlent, on peut citer : l’enroulement des cornes des défenses, la structure des rayons de miel et des toiles d’araignée, l’arrangement des coquilles et des ailes de libellules, entre autres merveilles.

Dans cet exercice on s’intéresse particulièrement aux coquillages et à leurs modèles. Mots-clés : spirale équiangle, progression géométrique, progression arithmétique, hélico-spirale. Enoncé L’exercice s’inspire du livre Forme et croissance de D’Arcy Thompson, Seuil, 1994 et The Algorithmic Beauty of Sea Shells de Hans Meinhardt, Springer, 1995. Dans la préface du livre Forme et croissance, Stephen Jay Gould décrit ce chef d’œuvre : D’Arcy Wentwoth Thompson (1860-1948), professeur de zoologie à l’université de Saint Andrews en Ecosse et peut-être l’esprit le plus universel de ce siècle, ne fut pas homo unius libri (l’homme d’un seul livre), loin s’en faut. Utiliser les mathématiques et la mécanique pour expliquer comment les coquilles de bivalves s'emboîtent si bien. 32 Des spirales et des fleurs.
Résumé : un capitule de tournesol, comme celui d’une pâquerette, ou bien les dispositions des écorces des pommes de pin présentent des familles de spirales qui s’interpénètrent.

Le sens d’enroulement étant opposé. Des modélisations permettent de reproduire ce phénomène particulièrement fascinant. Spirales végétales. On observe des spirales dans divers végétaux.
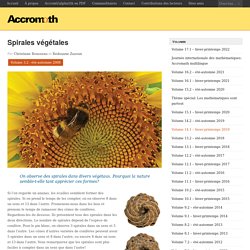
Pourquoi la nature semble-t-elle tant apprécier ces formes? Si l’on regarde un ananas, les écailles semblent former des spirales. Pourquoi les abeilles sont bonnes en maths. As-tu déjà eu la chance d’étudier l’intérieur d’une ruche ?
C’est une action périlleuse qu’il convient d’effectuer avec prudence et le moins souvent possible. En effet, ouvrir une ruche est perçu par les abeilles qui y vivent comme une agression, une attaque contre leur logis et c’est bien compréhensible : personne n’a envie qu’un géant retire le toit de sa maison ou de son appartement pour regarder à l’intérieur, voire se servir dans le frigo ! Il faut dire aussi qu’une ruche recèle de nombreux trésors : depuis longtemps l’être humain s’en nourrit. Regardons en particulier le fruit du travail de nos ouvrières en bâtiment : constitués de multiples cellules en forme d’hexagone (c’est-à-dire ayant six côtés bien droits) qu’on appelle des alvéoles, les rayons de cire qu’elles bâtissent remplissent plusieurs fonctions. Conférence d'Olivier Piazza (parle de la danse en 8 des abeilles) [Conférence SML] Partitionnement optimal: Des nids d'abeille aux condensats de Bose-Einstein.
Paraboloïde elliptique. PARABOLOÏDE ELLIPTIQUEElliptic paraboloid, elliptisches Paraboloid Les paraboloïdes elliptiques peuvent être définis comme les surfaces engendrées par la translation d’une parabole (ici de paramètre p) le long d’une parabole de même sens (ici de paramètre q) (ce sont donc des surfaces de translation).

Remarquons que lorsque les deux paraboles sont de sens contraire, on obtient le paraboloïde hyperbolique. Les □cigales□ sont-elles bonnes en maths ? (OUI) La loi surface-volume, ou l'origine des oreilles de l'éléphant et de la force de la fourmi. Fractales. Comprendre l’équilibre de Hardy Weinberg. TP 7 Comprendre l’équilibre de Hardy Weinberg A la fin de la séance : je sais modéliser une population pour visualiser le modèle théorique de HWj’ai compris comment évoluent les fréquences alléliques au cours des générations.
Matériels : Logiciel de modélisation multi-agents : Edu’Modèles ;Fichier « calculs_frequences_alleles.xls » permettant le calcul des fréquences alléliques à partir des génotypes ; fiche technique du logiciel Edu’Modèles. En 1908, le mathématicien britannique Geoffroy Hardy et le médecin allemand Wilhelm Weinberg proposent un modèle théorique qui prévoit que la fréquence des allèles et celle des génotypes d’une population sont constantes. Modélisation de la croissance des micro-organismes - Inria. Conférence 6 « Mathématiques de la propagation en sciences de la vie » - Vincent CALVEZ, Mathématicien, directeur de recherche Institut Camille Jordan, Lyon/Saint-Etienne - Présentation Christophe CAPDEVIELLE, IA-IPR.
Dynamique des populations de prédateur et de proie, selon le modèle de Lotka et Volterra. La suite logistique. Pour chercher et approfondir - L’application logistique : une suite au comportement chaotique. Moreau Emmanuel Résumé de l’article Cet article est la suite de l’article du même auteur publié dans le n°460 du Bulletin vert de l’APMEP, sous le même titre rapportant les réflexions menées avec un groupe d’élèves travaillant dans le cadre d’un TPE sur le thème hasard et chaos avec un logiciel de calcul formel.
L’auteur revient ici sur les valeurs particulières, donne une analyse statistique puis étudie la distribution des valeurs de la suite. D. Perrin - La suite logistique et le chaos. UNE VERSION DE LA CONJECTURE DE KENDALL. Construction de la mosaïque de Voronoï Plaçons-nous dans un carré (disons de côté 1), et prenons deux points, et , dans ce dernier, comme dans la figure ci-dessous. Nous y avons également tracé, en rouge, la portion de la médiatrice qui se situe dans le carré. C’est en fait le lieu où l’on est aussi proche de que de . Les points communs entre les oiseaux et les. PHÉNOMÈNES D'ALIGNEMENT BANCS DE POISSONS, NUÉES D'OISEAUX (...) - Frouvelle - Math Park - 16/03/19. DES DONNÉES BIOLOGIQUES AUX MODÈLES ET INVERSEMENT. Chaque examen produit des variables d’intérêt pouvant être des images médicales, des concentrations moléculaires ou des états cliniques.
L’ensemble de ces données peut alors être considéré comme une entrée. Le but est de comprendre comment cet ensemble impacte un paramètre de sortie à définir. Modélisation mathématique pour l’écologie. [Dominique Gibert] L'auscultation et la surveillance des volcans. INSA 3BS R Biomathématique, modélisation par les Equations Différentielles Ordinaires (EDO) Feux foret. Modélisation des feux de forêt. Feu de forêt en Corse. Les feux de forêt représentent un risque majeur pour de nombreux pays dans le monde. Outre les pertes de vie humaines, ils occasionnent des dégâts environnementaux et économiques (destruction de biens d’habitation et de moyens de lutte contre les feux). Ils sont la cause de déforestations et de désertifications, et polluent l’air : les émissions de CO2 lors d’un feu de forêt représentent 20 % des émissions totales, sans compter les métaux lourds et radionucléides qui sont aussi propulsés dans l’atmosphère.
Ces dernières années, le feu a engendré de nombreuses catastrophes dans le monde entier : au début de l’année 2013 en Australie, plus de 200 km2 de forêts et de terres agricoles ont été détruits par un incendie qui a contraint 2 000 personnes à quitter leur logement. Modéliser la propagation des ondes sismiques dans le sol. Tremblement de terre de Mexico, 1985. Il est encore difficile de prédire les séismes (voir ici). On peut par contre essayer de réduire le risque sismique, c’est-à-dire les conséquences humaines et matérielles en adaptant les constructions à la probabilité pour une région donnée de subir un séisme.
Le développement de méthodes numériques pour simuler sur ordinateur la propagation des ondes sismiques depuis la source du séisme jusqu’aux habitations permet aujourd’hui d’aider à la définition de règles de constructions parasismiques. Cours d'ACP : théorie et pratique. Martingales et calcul stochastique. Université d'Orléans Master 2 Recherche de Mathématiques, 2012-13 Martingales et calcul stochastique Lundi, 9h30-13h00, salle L6 Cours les 10/9, 24/9, 8/10, 22/10, 12/11, 26/11, 10/12 Travaux dirigés les 17/9, 1/10, 15/10, 5/11, 19/11, 3/12, 17/12 (J. -B. Probabilité d'extinction d'une espèce menacée. LA PROBABILITÉ D’EXTINCTION D’UNE ESPÈCE MENACÉE : UNE ILLUSTRATION. LES MATHÉMATIQUES DE LA MORPHOGÉNÈSE (I)
LES MATHÉMATIQUES DE LA MORPHOGÉNÈSE (II) L’ÉVOLUTION DARWINIENNE EN ÉQUATIONS ? Séduction entre les cygnes - Loi somme, produit, probabilité conditionnelle, événement contraire. CALCULER SANS NEURONE. Albert Goldbeter : L'horloge circadienne. DANIEL BERNOULLI, PIONNIER DES MODÈLES MATHÉMATIQUES EN MÉDECINE. Thi : un médecin parle des maths.
Epidémie et Covid. Tests Statistiques. BIO-STATISTIQUES. Plutôt SVT.