

Équations de prédation de Lotka-Volterra. En mathématiques, les équations de prédation de Lotka-Volterra, que l'on désigne aussi sous le terme de « modèle proie-prédateur », sont un couple d'équations différentielles non-linéaires du premier ordre, et sont couramment utilisées pour décrire la dynamique de systèmes biologiques dans lesquels un prédateur et sa proie interagissent.
Elles ont été proposées indépendamment par Alfred James Lotka en 1925[1] et Vito Volterra en 1926[2]. Ce système d'équations est classiquement utilisé comme modèle pour la dynamique du lynx et du lièvre des neiges, pour laquelle de nombreuses données de terrain ont été collectées sur les populations des deux espèces par la Compagnie de la baie d'Hudson au XIXe siècle.
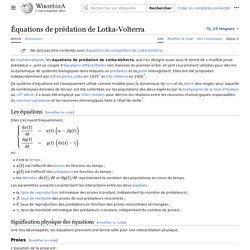
Il a aussi été employé par Allan Hobson pour décrire les relations entre les neurones cholinergiques responsables du sommeil paradoxal et les neurones aminergiques liées à l'état de veille[3]. Les équations[modifier | modifier le code] Elles s'écrivent fréquemment : où . . Ou qui vérifie et à avec. Cours equaDiff. Dynamique des populations. Il peut sembler paradoxal de modéliser l'évolution dans le temps de la taille d'une population, qui est un nombre entier d'individus, par la solution d'une équation différentielle, qui est nécessairement une fonction continue (et même dérivable).

Une population animale évolue par les naissances et les décès, qui la font augmenter ou diminuer chaque fois d'une unité. Mais pour une population de grande taille, et selon l'échelle de temps à laquelle on se place, les variations de la population pourront effectivement apparaître comme continues. Concernant la population humaine sur la terre, de l'ordre de milliards individus, les nombres de naissances et de décès qui ont lieu chaque seconde sont de plusieurs milliers. Ces nombres, même s'ils ne sont pas définis très rigoureusement, sont compris par chacun comme des moyennes sur les secondes contenues dans un intervalle de temps suffisant.
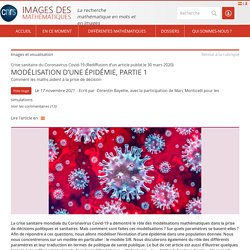
Secondes dans un jour, dans une année. La population de la terre à l'instant secondes, vaut . . . Dossier épidémies Images des mathématiques (CNRS) Les mathématiques jouent un rôle très important en épidémiologie puisqu’elles permettent de modéliser les épidémies.

Vous trouverez dans ce dossier quelques articles concernant ces modèles, parfois à base d’équations différentielles, d’autres fois de nature probabilistes, etc. Voici également quelques références que nous suggérons. Une web-conférence donnée par Philippe Sansonetti au Collège de France le 16 mars 2020 : Covid-19 ou la chronique d’une émergence annoncée. La leçon inaugurale d’Arnaud Fontanet au Collège de France : L’épidémiologie, ou la science de l’estimation du risque en santé publique.
Une séance spéciale à l’Académie des sciences sur le coronavirus. Pour d’autres références encore, on pourra également consulter cette page de la SMF. Images des mathématiques : la propagation d'une épidémie. Pour les États et pour les organisations internationales, comme l’Organisation mondiale de la santé (OMS) ou l’Union européenne (UE), connaître l’évolution d’une épidémie humaine (grippe H1N1, virus Ebola, coronavirus), animale (grippe aviaire, peste porcine, rage) ou végétale est primordial.
Modéliser le réchauffement climatique. Comment arrive-t-on à fixer des cibles à atteindre pour la réduction de gaz à effet de serre?

Quel est l’impact de les négliger? Ou même d’en dévier un peu? Pour répondre à de telles questions, on gagne à se tourner vers la modélisation et la simulation. Un monde en profond changement Pour avoir une idée de ce que nous réserve l’avenir, il est souvent d’usage d’extrapoler à partir du passé. C’est le cas avec les changements climatiques qui résultent de l’impact des activités humaines sur l’environnement.
De tous les phénomènes associés aux changements climatiques, nous avons choisi d’examiner de plus près le réchauffement planétaire. Etienne Pardoux : Modèles mathématiques des épidémies – Briques2math. Etienne Pardoux, Professeur émérite à Aix Marseille Université, nous parle de modélisation mathématique des épidémies.
Les mathématiques détaillées et explications sont dans le texte qui suit ! Introduction Etienne Pardoux : Nous vivons en ce moment une pandémie mondiale inédite. Une addition d’épidémies dans chaque pays, qui se sont répandues par les transports aériens, et qui deviennent des épidémies nationales une fois les frontières verrouillées. Dans la plupart des pays, on en est encore au début de l’épidémie, et on voudrait savoir jusqu’où la courbe des infectés et des décès va grimper, et quelle est l’efficacité des mesures de confinement décidées dans la plupart des pays.
Sujets Grand Oral mathématiques et SVT. Math et Covid 19 : Le R0 et la croissance exponentielle. Tests de dépistage du covid 19 : l'éclairage des probabilites conditionnelles.