

Sujets Grand Oral mathématiques et SVT. Comment réussir le Grand Oral Spé Maths : Les probabilités au service des Tests diagnostiques. Grand oral : "A quoi sert le principe de Hardy-Weinberg ?" Grand Oral (maths/SVT) : "Comment peut on étudier l'évolution d'une population de bactéries ?" Grand Oral de Maths : équations logistiques et évolutions de populations. A quoi ça sert les maths : Modéliser l'épidémie de covid19. 200 SUJETS DE GRAND ORAL. Les mathématiques dans la biologie. Avec nos partenaires, nous traitons vos données pour les finalités suivantes : le fonctionnement du site, la mesure d'audience et web analyse, la personnalisation, la publicité et le ciblage, les publicités et contenus personnalisés, la mesure de performance des publicités et du contenu, le développement de produit, l'activation des fonctionnalités des réseaux sociaux.
Vos préférences seront conservées pendant une durée de 6 mois. Nature fractale. Mathématiques pour la biologie (cours) L’histoire de la démarche scientifique. Méthode et démarche scientifiques. Maths En Scène / Maths et nature (Partie 1) Maths En Scène / Maths et nature (Partie 2) Les algorithmes du vivant. Une planète vivante Archives. Géologie et géophysique Archives. Océans et atmosphère Archives.
Beautés universelles: simplicités et symétries. Abeilles et Maths. La merveilleuse présence des mathématiques dans la nature. Avez-vous déjà observé la forme d’une fleur de tournesol, la structure d’un flocon de neige ou la morphologie d’une fougère ?
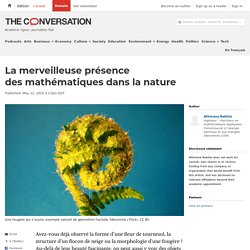
Au-delà de leur beauté fascinante, on peut aussi y voir des objets mathématiques, puisque les spirales de la fleur de tournesol suivent une célèbre suite numérique appelée suite de Fibonacci, les flocons de neige présentent des symétries hexagonales particulières et la morphologie de la fougère décrit une géométrie fractale. De nombreux autres exemples illustrent à quel point les objets mathématiques sont présents dans la nature. Nature et algorithmes. De la nature à l’informatique. Algorithmes - Claire Mathieu. Sylvain : un biologiste parle des maths.
Varipon alias Yutaca Sawaï.
Modélisation du mouvement animal. Maths et biologie 2014. Savoirs ENS. La perception de la couleur chez l'être humain. Saguenay. G modelisation. Neural Networks and the Backpropagation Algorithm – Math ∩ Programming. Equations Differentielles. FDM PASS. L’inéluctable évolution des génomes au sein des populations - Tle - Cours SVT. Des calculatrices pour presque tout ! 51 Une foret fractale. Résumé : en partant de la relation d’Euler et en manipulant des nombres complexes, on peut produire des images fractales très belles qui rappellent des forêts.

Mots-clés : nombre complexe, relation d’Euler, fractal. Enoncé. Ordre et désordre. Plongée dans L'INFINIMENT GRAND. Plongée dans L'INFINIMENT PETIT.
Ecologie Archives - MATH'MONDE, le blog d'Hervé LEHNING, agrégé de mathématiques. Jean-Henri Fabre est connu pour son observation des insectes.

Excellent vulgarisateur, il est de ceux qui savent communiquer leurs passions. Les mathématiques en font partie. Course: Ressources pour des projets interdisciplinaires en sciences (dossiers), Topic: Dossier Anthropologie légale "BONES" Course: Ressources pour des projets interdisciplinaires en sciences (dossiers), Topic: Dossier L'entomologie légale. [Conférence SML] Des probabilités pour le vivant - Vincent Bansaye. Les phénomènes aléatoires dans l'expression du gène chez les bactéries. Les différentes étapes de la fabrication d’une protéine.

Les bactéries sont des organismes unicellulaires présents dans tous les milieux, y compris les plus hostiles comme les fonds marins ou encore notre intestin. Une bactérie est, en première approximation, une cellule composée d’une chaîne d’ADN baignant dans un milieu visqueux, le cytoplasme, avec d’autres composants comme les ARN, les protéines, etc… Les protéines sont les éléments-clés de la vie cellulaire pour tous les organismes vivants.
L’expression maintenant fameuse de F. Crick en 1958, le «dogme central de la biologie moléculaire», affirme que l’information biologique est à sens unique de l’ADN, vers les ARN et ensuite vers les protéines. À chaque protéine est associée une section de l’ADN, le gène, qui contient le «code» de la protéine. Séduction entre les cygnes - Loi somme, produit, probabilité conditionnelle, événement contraire. LA PROBABILITÉ D’EXTINCTION D’UNE ESPÈCE MENACÉE : UNE ILLUSTRATION. Piste rouge Le 9 juin 2020 - Ecrit par Catherine Combelles Lire l'article en Les articles d’Images des maths sont une ressource intéressante pour le professeur du secondaire.

Mais il y a loin d’un article de vulgarisation même simple à une activité pour la classe. Le professeur a toujours besoin de sujets intéressants, mais il est soumis à de nombreuses contraintes : le programme, le niveau de la classe le nombre d’élèves, le temps dont il dispose. Probabilité d'extinction d'une espèce menacée. Les modèles d’évolution de populations ont une longue histoire [1].
La suite de Fibonacci fut introduite au XIII siècle par Léonard de Pise pour décrire la croissance d’une population de lapins. Le modèle le plus connu d’évolution de populations est sans doute celui de Malthus, proposé au début du XIX siècle. Supposons que chaque année, des individus de la population donnent naissance à un enfant, et que meurent. L’augmentation nette sera donc de , ce qui conduit à une croissance exponentielle, comme pour les intérêts composés d’un compte d’épargne [2]. Martingales et calcul stochastique. Université d'Orléans Master 2 Recherche de Mathématiques, 2012-13 Martingales et calcul stochastique.
Probabilités Archives. LE HASARD & LA COMPLEXITÉ DES LOGIQUES DU VIVANT. Le hasard décrypté par des scientifiques. FMV 2017 : De l'analyse comme langage pour les autres sciences. Competences maths pc svt. Biostatistique. Un article de Wikipédia, l'encyclopédie libre.
La biostatistique (mot-valise issu des champs de la biologie et des statistiques) est un champ scientifique constitué par l'application de la science statistique à la biologie et à la médecine. Variantes[modifier | modifier le code] Le domaine d'application des biostatistiques est large. Il peut s'agir de biométrie, de conception méthodologique d'études biologiques ou cliniques, ou encore du recueil, de l'analyse et du traitement statistique de données recueillis lors d'études écologiques, biologiques, agronomiques, halieutiques, de santé publique, de santé environnementale, d'études épidémiologiques, médicales et/ou cliniques, pharmaceutiques, agropharmaceutiques... Index SMEL. BIO-STATISTIQUES. Modélisation mathématique pour l’écologie. Modèles numériques. Modéliser le rôle joué par le moustique dans la transmission du paludisme par Philippe Cosentino Place dans le programme En classe de seconde, les maladies vectorielles, c’est à dire pour lesquelles l’agent pathogène est transmis par un vecteur animal, font partie des notions explicitement attendues.
Extrait du B.O. : Certaines maladies causées par des agents pathogènes sont transmises directement entre êtres humains ou par le biais … Lire la suite Présentation de Géné’pop, logiciel généraliste de génétique des populations. Cos(φ)log. Microscope polarisant virtuel - Minéralogie. INSA 3BS R Biomathématique, modélisation par les Equations Différentielles Ordinaires (EDO) Albert Goldbeter : L'horloge circadienne. Des algorithmes pour dépister le dopage. La lutte antidopage se dote d’un tout nouvel outil : un modèle informatique qui, à partir de l’historique des performances d’un sportif, permet de repérer s’il s’est dopé. Il a été développé au laboratoire I3S qui vient de recevoir un trophée de l'Inpi. Une nouvelle arme numérique dans la lutte contre le dopage ! Une équipe du CNRS, en collaboration avec des médecins de l’International Association of Athletics Federations (IAAF)1, a développé un outil numérique capable de détecter un éventuel usage de substances illicites par un sportif.
Compléter le passeport biologique. Cours M2 algorithmes évolutionnaires. ALGORITHMES EVOLUTIONNAIRES ET APPLICATIONS EN SCIENCE DU VIVANT Université Pierre et Marie Curie Master de Sciences & Technologies M2 Mathématiques & Applications Parcours ANEDP ou MBIO Laurent Dumas Ce cours présente différents types d'optimisation par algorithmes évolutionnaires ainsi que leurs applications à plusieurs problèmes en sciences du vivant ou en ingénierie.
Mardi 19 Janvier 2010, 11h15-13h15 : 1.1 Quatre problèmes d'optimisation 1.1.1 Configuration d'une molécule d'énergie minimale 1.1.2 Construction d'une fibre optique aux propriétés optimales 1.1.3 Décodage d'une image de code barre floue et bruitée 1.1.4 Ecoulement sanguin dans les artères: un modèle optimal Mardi 26 Janvier 2010, 11h15-13h15 : 1.2 Quelques rappels sur les méthodes de descente 1.3 Deux méthodes déterministes d'optimisation sans gradient 1.3.1 Méthode de Nelder Mead 1.3.2 Méthode de Torczon Mardi 02 Février 2010, 11h15-13h15 : 1.4 Le recuit simulé 1.4.1 Principe. Lynx. CONJECTURE DE SWINNERTON-BIRCH-DYER ET OLFACTION DES LIMACES. Le 1er avril 2013 - Ecrit par Un jour une brève Cet article a été écrit en partenariat avec Mathématique de la planète Terre Le site Mathématiques de la Planète Terre (MPT), aujourd’hui Brèves de maths, a proposé, durant toute l’année 2013, une brève quotidienne avec « pour objectif d’illustrer la variété des problèmes scientifiques dans lesquels la recherche mathématique actuelle joue un rôle important, ainsi que certains grands moments dans l’histoire des sciences où les mathématiques ont, en interaction avec les autres sciences, aidé à comprendre ce que nul n’avait compris jusque-là. »
1968 : la théorie des catastrophes. La théorie des catastrophes est la théorie mathématique des modifications spectaculaires ou soudaines. Les mathématiciens Tim Poston et Ian Stewart fournissent des exemples : « Le grondement d'un tremblement de terre, la densité critique de population en dessous de laquelle certaines créatures se développent comme sauterelles et au-dessus comme criquets... Le rythme de reproduction change brusquement, et ne cesse de doubler, de façon cancéreuse. Un homme est pris d'une vision sur le chemin de Damas ». De la molécule à l'odeur : les bases moléculaires des premières étapes de l'olfaction - L'Actualité Chimique. Mots-clés : Odeur, molécule, olfaction, arômes, parfums, chimie bio-organique, relations structure/odeur, gènes des récepteurs olfactifs.
Keywords : Odour, olfaction, flavour, fragrance, scent, bio-organic chemistry. Le prix Nobel 2004 de physiologie ou de médecine est venu récompenser les travaux de deux chercheurs américains, Richard Axel et Linda Buck, pour leur découverte en 1991 de la famille de gènes des récepteurs olfactifs et des premiers niveaux de traitement de l’information par le système olfactif. Nous utilisons le coup de projecteur ainsi donné aux recherches sur l’olfaction pour faire le point sur les avancées récentes qui débouchent sur une meilleure compréhension des aspects moléculaires de la chimioréception. De la molécule à l’odeur. POURQUOI L’AIRE DE RÉPARTITION DE CERTAINES ESPÈCES EST LIMITÉE ? LE PHYTOPLANCTON : UN MONDE MICROSCOPIQUE EN ÉVOLUTION. Statistique et santé publique. PHÉNOMÈNES D'ALIGNEMENT BANCS DE POISSONS, NUÉES D'OISEAUX (...) - Frouvelle - Math Park - 16/03/19.
Paraboloïde elliptique. LA CHENILLE DE L’ÉPICÉA. Vagues, tourbillons, tsunamis. Hasard et glaciations. Modéliser et simuler la fonte des calottes polaires - Interstices.
4BIM-PUJO. Pour chercher et approfondir - À propos du daltonisme. Jeu de la vie, automates cellulaires. Mouvements browniens et mouvements de foules. Shannon Théorie de l'information. Biomeca - Centre de masse segmentaire. Modélisation mathématique en biologie : un exemple. Intégrité scientifique. Corrélation Causalité. Incertitude. Conférence : "Les mathématiques pour vivre mieux' LES ONDES, AUX ORIGINES DE LA MAGIE DES MONDES. Ondes et signaux. [Conférence SML] Des probabilités pour le vivant - Vincent Bansaye. 8/12 La biologie à la lumière du désordre. Vers une (nécessaire) réconciliation des mathématiques et de la biologie ?