

Q4: How does Netflix recommend movies? The Netflix Prize Netflix is a successful DVD rental and online streaming company.
In 2006, Netflix wanted to improve their movie recommendation system to increase customer satisfaction and to get customers to watch more movies. They announced a competition to improve their current recommendation system, Cinematch, by 10%, with a one million dollar prize. Learning, Predictive Power, and Overfitting. This example hopes to illustrate the notions of learning, predictive power, and overfitting.

Bear with the formatting and verbosity for now... Suppose you get a phone call one morning telling you that the stock market will rise that day. Amazon and Youtube's Recommendation Systems. Intro Recommendation systems are among the most important algorithms in popular websites today.

They contribute to the site way in nearly every useful way: They keep users on the site longer, create greater investment from the user into the site, allow him to view more ads, and keep the user coming back to the site. How does Internet Radio (Pandora) work? Pandora Internet Radio In late 1999, Tim Westergreen and Will Glaser conceived the "Music Genome Project", and, after joining forces with Jon Kraft, they founded the marketable "Pandora Media" project.
Pandora Radio, launched in 2007, is now one of the leading online internet radio providers in the United States, Australia and New Zealand, with a user base of around 54.9 million (in July 2012) and a net income of around 16 million dollars (in 2012). Pandora has both a desktop (online and offline) streaming platform, as well as a mobile one (apps available for iOS, Android, Blackberry and Windows mobile. Q5: When can I trust an average rating on Amazon? Rating on Amazon Amazon shows a ranking to consumers and it helps to them to decide on the purchase of products.
The ranking assigned to each product is a rational scalar within a range that goes from 1 to 5, it is obtained by applying an algorithm based on Amazon's users reviews, they include three factors: Rating (it is a natural scalar within a range that goes from 1 to 5). Reviews. Reviews of reviews. Overview of Reputation Systems. With the exponential increase in the amount of information on the Internet, we have access to huge number of articles, products, reviews and comments nowadays.
However, the problem that came along with this seemingly great benefit is trust. Among the different product reviews or news articles, which one should we trust and how do we make this choice? Other rating systems. What if your data doesn't come in numeric form, but rather in the form of binary comparisons?
This happens in several cases, but the two most common are two-player games (Alice defeats Bob and Bob defeats Carol; how do we rate the players?) And "pic battles" such as thecutest.info, in which users repeatedly vote on which of two choices should be rated higher. While the two problems are effectively the same, different algorithms have been developed for each use case, depending on whether we view it as a rating problem or a voting problem. Chess-specific rating systems. A Proof of the Rule of Succession. In this section we shall show an explicit proof for Laplace's "rule of succession," which states: "given that you find and flip a biased coin $n$ times, resulting in $s$ heads, the probability that the next flip will turn up heads is $\frac{s+1}{n+2}$".
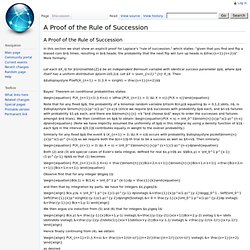
More formally: Let each $X_i$ for $i\in\mathbb{Z}$ be an independent Bernoulli variable with identical success parameter $p$, where $p$ itself has a uniform distribution $p\sim U(0,1)$. Let $X = \sum_{i=1}^{n} X_i$. Then: $$\displaystyle P\left(X_{n+1} = 1\ |\ X = s\right) = \frac{s+1}{n+2}$$ Bayes' Theorem on conditional probabilities states:
Q6: Why does Wikipedia even work? History and Background Wikipedia is an extremely popular online encyclopedia launched in 2001, founded by Jimmy Wales.
It currently has over 4 million article in English alone (though as many as half are very short articles called "stubs. ") Wikipedia is free and open to anyone to edit. Wikipedia was not the first online encyclopedia, but it has become wildly successful. Wikipedia does not have rigid fact-checking procedures, nor is it limited to editing only be experts or specialists. Why it "works" Network Effect Wikipedia benefits tremendously from the network effect. Arrow's impossibility result. Background With voting systems, we apply on a set of given options a list of individual preferences in order to extract an global preference order.
In these voting systems, there are a set of standard qualities we would like our voting systems to abide by. Yet, when voters have three or more distinct alternatives, we find that it is impossible for a voting system to satisfy a generally-agreed upon set of properties. Since these properties are generally believed to be key to every voting system, this theorem shook the world of decision making and changed the way we analyze voting systems. Properties. Voting Systems that Satisfy the "Impossibility Criteria" We talked about Arrow's and Sen's Impossibility Results in class, and it was mentioned that no common voting systems satisfy either of the sets of conditions.
Arrow's Impossibility Theorem states that no rank order voting systems satisfies the following conditions (directly quoted from the reference given): -If every voter prefers alternative X over alternative Y, then the group prefers X over Y. -If every voter's preference between X and Y remains unchanged, then the group's preference between X and Y will also remain unchanged (even if voters' preferences between other pairs like X and Z, Y and Z, or Z and W change). El Farol Bar Game and Negative Externalities. The Problem With Two Analogies The El Farol Bar Game is named after a bar in Santa Fe that used to have live music every Thursday evening.
In the context of the problem, on Thursday evenings, they could not have more than 60 people in the bar to hear the live music. When more than 60 people show up on Thursday to hear the live music, it gets too crowded and therefore unpleasant to attend. Prisoner's Dilemma Comes to Mass Media. In December of 2012, TV celebrity Howie Mandel was the game show host for a special 6 night holiday run of a new game show called "Take It All" which aired on NBC.
Take It All is the first game in the US that utilizes the classic Prisoner's Dilemma. Undermining Voting Systems. We have learned about several voting methods in class - plurality, Condorcet, and Borda Count voting to name a few - and ultimately settled on the Borda Count as one of the systems that satisfies all of Arrow's Five Axioms, if we change the Independence of Irrelevant Alternatives axiom (IIA) to its Intensity Form (IIIA). But as it turns out, Borda Count and its counterparts are susceptible to a number of subversive strategies that can change the outcome to the benefit or detriment of a desired candidate(s).