

Hardy qui a lu la lettre de Ramanujan a pensé que le contenu était initialement un radotage insensé, mais parce que la lettre l'a saisi par le cœur, Hardy l'a présenté à son compatriote Littlewood. Après avoir réfléchi à la lettre pendant plusieurs heures, ils ont jugé que Ramanujan avait une intelligence extrêmement élevée, personne n'est un match pour lui.
Ainsi, ils ont envoyé un messager en Inde et ont commencé à travailler pour apporter le mystérieux talent unique de l'Inde à Cambridge.
Hardy a demandé à Ramanujan comment il avait trouvé des formules ésotériques, Ramanujan a dit: "Quand je rêve, ma déesse Namagiri Thayar enveloppe les formules sur ma langue." Il'était un hindou pieux.
Hardy pensait que si Ramanujan avait grandi avec une éducation britannique, il deviendrait un grand mathématicien, mais c'est médiocre et ce n'est pas la nature divine de Ramanujan.
Des années plus tard, Paul Erdős nous a transmis les notes personnelles de Hardy sur les mathématiciens. Supposons que nous évaluions les mathématiciens sur la base du talent pur sur une échelle de 0 à 100, Hardy s'est donné un score de 25, Littlewood 30, Hilbert 80 et Ramanujan 100.
Srinivasa Ramanujan. Suite au commentaire de Varipon: de Hardy à Ramanujan. Nombre taxicab. En mathématiques, le nième nombre taxicab, ou nombre de Hardy–Ramanujan, noté Ta(n) ou Taxicab(n), est défini comme le plus petit nombre qui peut être exprimé comme une somme de deux cubes positifs non nuls de n façons distinctes à l'ordre des opérandes près.
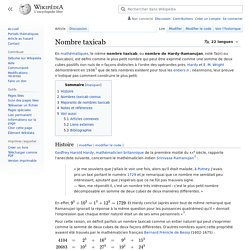
Hardy et E. M. G. H. Hardy. John Edensor Littlewood. Spirale d'Ulam. En mathématiques, la spirale d'Ulam, ou spirale des nombres premiers (dans d'autres langues, elle est appelée aussi horloge d'Ulam) est une méthode simple pour la représentation des nombres premiers qui révèle un motif qui n'a jamais été pleinement expliqué.
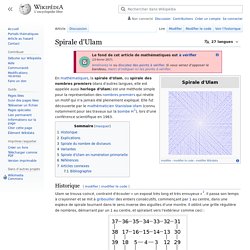
Elle fut découverte par le mathématicien Stanislaw Ulam (connu notamment pour ses travaux sur la bombe H[1]), lors d'une conférence scientifique en 1963. Historique[modifier | modifier le code] Première étape menant à la spirale d'Ulam : écrire les nombres naturels selon le sens inverse des aiguilles d'une montre. Nombres premiers jumeaux. En octobre 2019, les plus grands nombres premiers jumeaux connus, découverts en 2016 dans le cadre du projet de calcul distribué PrimeGrid[1], sont 2 996 863 034 895 × 21 290 000 ± 1 ; ils possèdent 388 342 chiffres en écriture décimale.
Définition[modifier | modifier le code] Soient p et q deux nombres premiers. On dit que (p, q) forme un couple de nombres premiers jumeaux si q = p + 2. Liste des premiers nombres premiers jumeaux[modifier | modifier le code] Suite des couples de nombres premiers jumeaux[2] jusqu'à 1 000 : DES JUMEAUX DANS LA FAMILLE DES NOMBRES PREMIERS III. Voici le troisième et dernier volet de notre série sur les nombres premiers jumeaux.

Dans le premier volet, nous avons commencé par observer l’agencement des nombres premiers, ces nombres strictement plus grands que qui ne sont divisibles que par eux-mêmes et . Parmi ces nombres premiers nous avons distingué ceux qui se suivent de deux unités comme et , et , et ... on les appelle nombres premiers jumeaux. Nous avons conjecturé qu’il y a une infinité de telles paires et dans le deuxième volet nous avons étayé cette conjecture en observant plusieurs graphiques. Aujourd’hui nous abordons de front la question fatidique : comment parvenir à une démonstration de cette conjecture ? Nombres premiers : des jumeaux, des cousins et... des nombres sexy. Petit exercice : recherchez tous les nombres premiers inférieurs à 60.
Comment avez-vous procédé ? Peut-être avez-vous testé pour chaque nombre s’il était divisible par un autre nombre que lui-même et 1, en faisant appel aux tables de multiplication ou même en utilisant une calculatrice ? Cela fonctionne, mais c’est long ! Une technique plus rapide est le crible d’Ératosthène. Elle consiste à éliminer, parmi tous les nombres, les multiples de 2, puis de 3, de 5... afin de ne conserver que les nombres premiers. Nombres premiers jumeaux : une version restreinte de la conjecture démontrée. Les nombres premiers sont un parfait exemple de concept mathématique simple donnant lieu à de nombreuses questions difficiles, voire non résolues.

Les nombres premiers sont les entiers positifs qui ont exactement deux diviseurs positifs (1 et eux-mêmes), comme 5, 7 ou 11. On sait, depuis Euclide, qu’il en existe une infinité. Mais qu’en est-il des paires de nombres premiers successifs, qui diffèrent de seulement 2 (comme 3 et 5 ou 11 et 13) ? Une conjecture affirme qu’il existe une infinité de telles paires de nombres premiers jumeaux. En 1849, le mathématicien français Alphonse de Polignac formule une version plus forte de cette conjecture : il existerait aussi une infinité de paires de nombres premiers qui diffèrent de 4 (comme 3 et 7), de 6 (comme 5 et 11), et ainsi de suite pour tout écart pair.
Nombres premiers. Namagiri Thayar. Namagiri Thayar (tamoul : நாமகிரித்தாயார்) est une forme de la déesse hindoue Lakshmi vénérée à Namagiri, une ville également appelée Namakkal, dans l'état moderne du Tamil Nadu, en Inde[1].
Dans la mythologie hindoue, elle est l'épouse de MahaVishnu. Namagiri et Srinivasa Ramanujan[modifier | modifier le code] Brahmanisme. La religion brahmanique ou brahmanisme ou encore appelée hindouisme ancien[1] correspond à la deuxième des trois phases historiques distinguées habituellement dans le développement de la religion des hindous[2].
Elle se situe après le védisme (env. 1500-500 avant notre ère) et occupe une période comprise entre -600 et 500 de l'ère courante[1]. Le terme « brahmanique » est dérivé de « brahmane » (brāhmaṇa), c'est-à-dire celui qui détient le Brahman[3]. Hindouisme. Lors des cérémonies religieuses hindoues (les pujas), des fleurs et des fruits sont offerts.
L’hindouisme[1] (hindi : hindu dharm ; devanāgarī : हिन्दू धर्म ; tamoul : இந்து சமயம் ; « religion hindoue »), ou sanatana dharma[2], (sanskrit IAST : sanātanadharma, en écriture devanāgarī : सनातनधर्म ; « Loi Éternelle »)[3], est l'une des plus anciennes religions du monde encore pratiquées[note 1] qui n'a ni fondateur, ni dogme imposé, ni institution cléricale organisée uniformément (les brâhmanes peuvent être de différentes écoles)[4],[5]. En 2015, le nombre de fidèles est estimé à 1,1 milliard[6],[7] dans 85 pays[8], c'est actuellement la troisième religion la plus pratiquée dans le monde après le christianisme et l'islam. Elle est issue du sous-continent indien[note 2] qui reste son principal foyer de peuplement. Le terme persan hindu (du sanskrit Sindhu) désignait au départ, pour les musulmans qui pénétrèrent en Inde, les habitants du bassin de l'Indus[8].
Lakshmi. Dans l'hindouisme, Lakshmi (sanskrit IAST : Lakṣmī ; « beauté, splendeur, prospérité, fortune[1] »), ou Mahalakshmi, est la déesse de la Fortune, de la prospérité, de la richesse et de l'abondance[2].
Elle est l'épouse de Vishnou. Son origine est associée à la déesse dénommée Sri citée dans le Rig-Véda[3]. Végétarisme. Un régime végétarien est dérivé de plantes, avec ou sans œufs ou produits laitiers. Plusieurs études font état d'un risque réduit de diverses maladies (notamment les maladies cardiovasculaires et le diabète insulinorésistant) et d'un risque global de mortalité réduit chez les personnes suivant un régime végétarien (ou quasi-végétarien), végétalien ou pesco-végétarien, par rapport à celles qui consomment régulièrement de la viande ; cette réduction du risque est plus marquée chez les hommes[4],[5],[6],[7],[8]. Selon d'autres études plus anciennes, cet effet positif est toutefois également observé chez les personnes non végétariennes attentives à leur santé, et pourrait être associé au style de vie général plus qu'à l'alimentation elle-même[9],[10].
Dans le langage courant, toutes les pratiques alimentaires excluant la chair animale mais incluant la consommation d'autres produits d'origine animale sont appelées « végétarisme » et leurs pratiquants « végétariens ». Notes : Ou encore : Gastronomie. La gastronomie associe l'art de bien préparer les repas, de sélectionner des produits plus ou moins travaillés (fromages, par exemple) et celui de les déguster. La gastronomie est la connaissance raisonnée de tout ce qui se rapporte à l'être humain en tant qu'il se nourrit. Certains restreignent cela à l'ensemble des règles (fluctuantes, selon pays, classes sociales et modes) qui définissent l'art de faire bonne chère[1]. Cet « art » de la bonne chère englobe ceux, créatifs dans certains cas, consistant à recueillir, adapter ou inventer des recettes, à sélectionner des produits, à préparer des plats, des mets et à les déguster.
Un « gastronome » est une personne qui cultive la gastronomie ; pour certains, ce serait un gourmand avisé, fort d'une culture de table. Étymologie[modifier | modifier le code] Monoculture et Polyculture. Maladie de la vache folle.