

Introduction aux nombres Premiers. FASCINANTS NOMBRES PREMIERS - 1. Combien existe-t-il de nombres premiers ? En janvier 2016, des mathématiciens américains ont découvert un nombre premier comptant plus de 22 millions de chiffres.

Mais combien existe-t-il au juste de ces nombres si particuliers ? Cela vous intéressera aussi [EN VIDÉO] Kézako : comment crypte-t-on les données sur Internet ? La cryptographie est la plus ancienne forme de chiffrement. On trouve des traces de son utilisation jusqu'en 2.000 avant J. Le plus grand nombre premier a été découvert ? Le 25 janvier, Dr Curtis Cooper, par l'intermédiaire du projet GIMPS, a découvert M48, le 48e nombre premier de Mersenne.

Ce nombre, 257 885 161-1, est donc officiellement aujourd'hui le plus grand nombre premier connu ! Le précédent record (M47, qui possède 12 978 189 chiffres) datait de 2008. Les nombres □ premiers. Le Mystère Des Nombres Premiers. Nombres premiers.
EPISODE 03 - Les nombres premiers. Les nombres premiers. Lesnombrespremiers. Les nombres premiers — Science étonnante #34. Les nombres premiers. Ma nouvelle vidéo porte sur le concept le plus simple et le plus déroutant des mathématiques : les nombres premiers !
Qu’est-ce qu’un nombre premier ? Une petite précision de définition pour commencer : je n’ai pas voulu alourdir l’introduction en donnant une définition totalement précise de ce qu’est un nombre premier. Et je suis passé notamment sur cette convention de ne pas considérer 1 comme un nombre premier. Math Park - 18/11/2017 - Olivier RAMARÉ - NOMBRES PREMIERS : UNE PROBLÉMATIQUE MODERNE (...)
Le plus grand nombre premier a été découvert ? Nombres premiers. Tout nombre non nul possède évidemment deux diviseurs : 1 et lui-même.
Il advient que dans le cas de l'unité ces deux diviseurs évidents se confondent. Or certains nombres ne possèdent pas d'autres diviseurs que ces deux diviseurs 'triviaux', on les appelle les nombres 'premiers' , c'est par exemple le cas de 2, 3, 5, etc... Les raisons pour lesquelles on refuse à 1 la qualité de nombre premier ne tiennent pas au fait que c'est le neutre de la multiplication mais plutôt au fait que c'est le seul élément inversible de ℕ. Il résulte de la théorie des anneaux que les éléments inversibles n'ont pas à être pris en compte pour les problèmes de décomposition (factorisation), faute de quoi on ne peut énoncer correctement les théorèmes.
Conjecture de Legendre. Nombres premiers : des jumeaux, des cousins et... des nombres sexy. Petit exercice : recherchez tous les nombres premiers inférieurs à 60.
Comment avez-vous procédé ? Peut-être avez-vous testé pour chaque nombre s’il était divisible par un autre nombre que lui-même et 1, en faisant appel aux tables de multiplication ou même en utilisant une calculatrice ? Cela fonctionne, mais c’est long ! Une technique plus rapide est le crible d’Ératosthène. Nombres premiers jumeaux : une version restreinte de la conjecture démontrée. Les nombres premiers sont un parfait exemple de concept mathématique simple donnant lieu à de nombreuses questions difficiles, voire non résolues.

Les nombres premiers sont les entiers positifs qui ont exactement deux diviseurs positifs (1 et eux-mêmes), comme 5, 7 ou 11. On sait, depuis Euclide, qu’il en existe une infinité. DES JUMEAUX DANS LA FAMILLE DES NOMBRES PREMIERS III. Voici le troisième et dernier volet de notre série sur les nombres premiers jumeaux.

Dans le premier volet, nous avons commencé par observer l’agencement des nombres premiers, ces nombres strictement plus grands que qui ne sont divisibles que par eux-mêmes et . Parmi ces nombres premiers nous avons distingué ceux qui se suivent de deux unités comme et , et , et ... on les appelle nombres premiers jumeaux. Nous avons conjecturé qu’il y a une infinité de telles paires et dans le deuxième volet nous avons étayé cette conjecture en observant plusieurs graphiques. Aujourd’hui nous abordons de front la question fatidique : comment parvenir à une démonstration de cette conjecture ? Commençons par oublier que ce problème est sans solution depuis près de deux siècles et réfléchissons ! DES JUMEAUX DANS LA FAMILLE DES NOMBRES PREMIERS I. Cet article est le premier volet d’une série de trois épisodes qui vise à présenter un problème mathématique célèbre et à ce jour irrésolu, celui des nombres premiers jumeaux.
Mais avant de parler de jumeaux, connaissez-vous les nombres premiers ? Il s’agit des nombres strictement plus grands que 1 qui ne sont divisibles que par 1 et par eux-mêmes : DES JUMEAUX DANS LA FAMILLE DES NOMBRES PREMIERS II. Voici le deuxième volet de cette série d’articles dédiée à la conjecture des nombres premiers jumeaux.
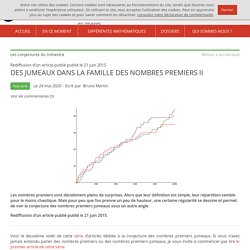
Si vous n’avez jamais entendu parler des nombres premiers ou des nombres premiers jumeaux, je vous invite à commencer par lire le premier article de cette série. Rappelons rapidement qu’une paire de nombres premiers jumeaux est constituée de deux nombres premiers dont la différence vaut . La liste de ces paires commence par : et on conjecture que cette liste ne s’arrête jamais, autrement dit qu’il y a une infinité de paires de nombres premiers jumeaux. Chemins Cloitre. KahaneGazette. UtiordiGazette. Progressions arithmetiques de nombres premiers consecutifs.
Le problème initial : le problème de Vavoda : Sur la division euclidienne d'un nombre premier par son rang : (Nik Lygeros, Michel Mizony et Paul Zimmermann) fichier.ps L'ANNONCE OFFICIELLE du 10-UPLET La publication : H.
Dubner, T. Forbes, N. LA RECHERCHE DU 10-UPLET : IL EST TROUVÉ le 2 Mars 98. LE PREMIER 9-UPLET TROUVÉ le 15 Janvier 98 LE PREMIER 8-UPLET TROUVÉ le 3 Novembre 97 Signalons que toutes ces progressions arithmétiques sont des solutions du problème de Vavoda. Collaboration entre Harvey Dubner, Tony Forbes, Nik Lygeros, Michel Mizony, Harry Nelson et Paul Zimmermann. Dans la presse, quelques sites. Quelques records en combinatoire et théorie des nombres. Retour à la page précédente. Nombres premiers sexy. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges A l'instar des nombres premiers jumeaux dont la différence est 2, deux nombres premiers n et p, n > p, sont dits sexy, si n - p = 6 (du latin sex = six, comme sexy, on l'a bien compris...). MarcDeleglise:MarcDeleglise. Soit θ et ψ les fonctions de Chebychev définies par θ(x)= Σp ≤ x log p et ψ(x) = Σpn ≤ x log p.
La métode évidente de calcul de theta(x), énumerer les nombres premiers ≤ x en additionnant leurs logarithmes est de coût proportionnel à x log(log x). La différence psi(x) - theta(x) = Σp^n ≤ x, 2 ≤ n, est une somme ne portant que sur les nombres premiers inférieurs à x^(1/2) par la méthode naïve elle se calcule en temps O(x^(1/2 + eps)) pour tout eps > 0. En utilisant alors l'algorithme de calcul de psi(x) en temps inférieur à O(x^(2/3 + eps) pour tout eps > 0, présenté dans M. Deléglise and J. Aa4946. DppGnbprem. Quadrature93. La conjecture de Goldbach. Tout nombre pair est la somme de deux nombres premiers Sous son apparente simplicité, cet énoncé en principe compréhensible par un enfant de 3ème (*) constitue en fait l’une des énigmes les plus importantes des mathématiques modernes. Cette affirmation porte le nom de « Conjecture de Goldbach », en référence au mathématicien prussien qui l’a pour la première fois énoncée en 1742, dans une lettre à Leonard Euler.
Ce dernier lui répondit qu’il considérait ce résultat comme « totalement certain, bien que je ne sois pas capable moi-même de le démontrer ». 268 ans plus tard, Euler peut dormir tranquille, personne n’a jamais réussi. Si vous vous sentez un peu fatigué pour chercher directement une démonstration, on peut s’échauffer en faisant quelques tests numériques. Combien les nombres entiers ont-ils de facteurs premiers : Denis CHOIMET. Indicatrice d'Euler (totient) ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Il s'agit de l'application, traditionnellement notée φ, qui à tout entier naturel n non nul associe le nombre d'entiers naturels inférieurs à n et premiers avec n : φ(n) = Card {k, k∈N, 1 ≤ k ≤ n - 1, pgcd(k,n) = 1} Math Park - 18/11/2017 - Olivier RAMARÉ - NOMBRES PREMIERS : UNE PROBLÉMATIQUE MODERNE (...)
Premiers. Math expo 1l. L'échiquier de Lucas-Lehmer - PeerTube. CONTER LES PREMIERS ! Test de primalité. La conjecture ABC. À première vue, la conjecture abc semble être d'une trompeuse simplicité. Elle énonce une certaine propriété sur trois nombres entiers naturels a, b et c liés par la relation la plus simple possible : a + b = c. Ce qu'elle affirme exactement n'est pas évident. L'idée est que si les facteurs premiers de deux nombres aet bse répètent beaucoup, il y a peu de chance pour que ce soit aussi le cas pour leur somme.
La conjecture abc a été énoncée en 1985 par Joseph Oesterlé, de l'Université Paris vi, et David Masser, de l'Université de Bâle, en Suisse. Malgré de solides indices en faveur de la validité de cette conjecture, aucune piste de démonstration ne semblait jusqu'ici très évidente, et la preuve paraissait encore éloignée. Conjecture de Legendre. Deux (deux ?) minutes pour... les nombres de Catalan. Math Park - 09/12/2017 - Viviane PONS - NOMBRES DE CATALAN. Math Park - 18/11/2017 - Olivier RAMARÉ - NOMBRES PREMIERS : UNE PROBLÉMATIQUE MODERNE (...) "Les mystères de la fonction zêta de Riemann" par Antoine Chambert-Loir. Deux (deux ?) minutes pour... l'hypothèse de Riemann. L’hypothèse de Riemann. Résumé rapide: la "démonstration" de l'hypothèse de Riemann. Hypothèse de Riemann. En mathématiques, l'hypothèse de Riemann est une conjecture formulée en 1859 par le mathématicien allemand Bernhard Riemann, selon laquelle les zéros non triviaux de la fonction zêta de Riemann ont tous une partie réelle égale à 1/2.
Hypothèse de Riemann. RiemannMar11. Les nombres premiers. NombresEntiersFev17. Les nombres premiers sont-ils (presque) aléatoires ? Actu 2. Mystères des nombres Premiers #2. Repartition des Nb premiers BEAMER. An example right from my number theory class. Protégez vos petits secrets grâce aux nombres premiers. Imaginons que vous soyez le chef de la diplomatie de votre pays, et que vos ambassadeurs aient besoin de vous envoyer des messages top secrets.
Afin d’échapper aux oreilles de l’ennemi et de Wikileaks, vous allez avoir besoin de coder ces messages. Comment faire ? La cryptographie basique Pour cela, vous pouvez choisir une méthode simple, comme substituer une lettre par une autre dans l’alphabet. C’est le principe qu’utilisait César pour communiquer avec ses généraux. Les méthodes de substitution simples sont malheureusement assez peu sûres car chaque lettre est toujours codée de la même manière : on peut donc casser ces codes en faisant de la statistique et en analysant les occurrences des lettres : ainsi en français, le E est la lettre qui doit revenir le plus souvent, suivie des lettres AIST, qui bien sûr sont elles-mêmes bien plus fréquentes que WXYZ. La cryptographie à clé Pour éviter cela, il faut un codage dans lequel une même lettre n’est pas toujours codée de la même manière.