

Test yourself! Amplitude and Period. Amplitude and Period Learning Objective(s) · Understand amplitude and period. · Graph the sine function with changes in amplitude and period. · Graph the cosine function with changes in amplitude and period. · Match a sine or cosine function to its graph and vice versa.

You know how to graph the functions and . Or , where a and b are constants. We used the variable previously to show an angle in standard position, and we also referred to the sine and cosine functions as . For the input (as well as to label the horizontal axis). . The Graphs of Sine and Cosine. A sine wave, or sinusoid, is the graph of the sine function in trigonometry.

A sinusoid is the name given to any curve that can be written in the form (A and B are positive). Sinusoids are considered to be the general form of the sine function. In addition to mathematics, sinusoidal functions occur in other fields of study such as science and engineering. This function also occurs in nature as seen in ocean waves, sound waves and light waves. Let's start with an investigation of the simpler graphs of y = A sin(Bx) and y = A cos(Bx). The value A affects the amplitude. The value B is the number of cycles it completes in an interval of from 0 to or 360º. Example: Amplitude and period transformations. Properties of The Six Trigonometric Functions.
4. Graphs of tan, cot, sec and csc. By M. Bourne The graphs of tanx, cotx, secx and cscx are not as common as the sine and cosine curves that we met earlier in this chapter. However, they do occur in engineering and science problems. They are interesting curves because they have discontinuities. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. [For more on this topic, go to Continuous and Discontinuous Functions in an earlier chapter.] Recall from Trigonometric Functions, that tanx is defined as: tanx=cos xsin x For some values of x, the function cosx has value 0.
Graphing Trigonometric Functions. Graphing Trigonometric Functions (page 1 of 3) Sections: Introduction, Examples with amplitude and vertical shift, Example with phase shift You've already learned the basic trig graphs.
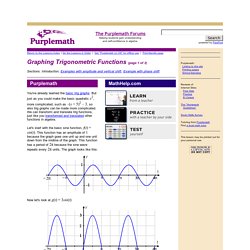
But just as you could make the basic quadratic x2, more complicated, such as –(x + 5)2 – 3, so also trig graphs can be made more complicated. We can transform and translate trig functions, just like you transformed and translated other functions in algebra. Let's start with the basic sine function, f(t) = sin(t). Now let's look at g(t) = 3sin(t): Do you see that the graph is three times as tall?
Now let's look at h(t) = sin(2t): Copyright © Elizabeth Stapel 2010 All Rights Reserved Do you see that the graph is squished in from the sides? Solving Trigonometric Equations. Solving Trigonometric Equations (page 1 of 2) Solving trig equations use both the reference angles you've memorized and a lot of the algebra you've learned.
Be prepared to need to think! Solve sin(x) + 2 = 3 for 0° < x < 360° Just as with linear equations, I'll first isolate the variable-containing term: sin(x) + 2 = 3 sin(x) = 1 Now I'll use the reference angles I've memorized: x = 90° Lesson HOW TO - Solve Trigonometric equations. Introduction The solution of trigonometric equations is one topic that students have particular problems with.
There are a few reasons for this: 1. there is usually a simplify part first that requires use of some TRIG identities. 2. there is the use of RADIANS rather than degrees, for which some students are not at ease with. 3. there is the repetitive aspect of TRIG functions that students find bewildering. All in all, a potentially daunting topic. To be honest though, there is nothing that you need fear here, so long as you take it methodically and slowly.
Also, you have to understand what it is you are doing. Solving the TRIG Equation Of the 3 topics listed above, I am concentrating on part 3, here in this Lesson. First thing, when solving a TRIG equation, is to understand or accept that each of SINE, COSINE and TANGENT have 2 angles that will satisfy the given equation within any 360 degree range. Basics This is difficult to explain, with no real picture to use, so bear with me. Done! Solving trigonometry equations using graphic methods.