(2) SOLVING TRIGONOMETRIC EQUATIONS
Note: If you would like a review of trigonometry, click on trigonometry. Example 1: Solve for x in the following equation. There are an infinite number of solutions to this problem. First isolate the cosine term. To solve for x, we have to isolate x. How do we isolate the x?
Amplitude, Period, Phase Shift and Frequency
Some functions (like Sine and Cosine) repeat forever and are called Periodic Functions. The Period is the length from one peak to the next (or from any point to the next matching point): The Amplitude is the height from the center line to the peak (or to the trough).
A-level Maths Trigonometry Revision - Graphs of trigonometric functions
The graphs of the three major functions are very important and you need to learn the characteristics of each. The sine function This graph is continuous (there are no breaks).
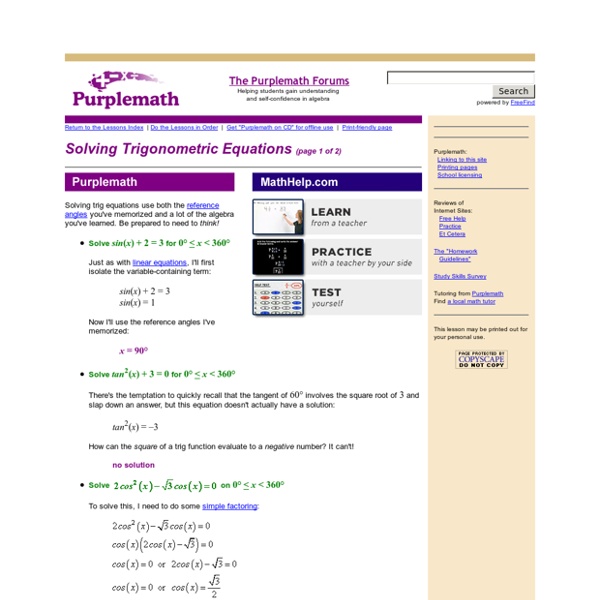
Solving Trigonometric Equations
This section covers: Solving trig equations is just finding the solutions of equations like we did with linear, quadratic, and radical equations, but using trig functions instead. We will mainly use the Unit Circle to find the exact solutions if we can, and we’ll start out by finding the solutions from We can also solve these using a Graphing Calculator, as we’ll see below.
Exploring y=Asin(Bx+C)+D
Assignment 1: Exploring Asin(Bx+C)+D by
(4) The Key Features of the Trig Graphs (Part 1)
In this section we will summarize what you have probably already discovered from generating the graphs of the trigonometric functions. However, we will use some important terminology that will help us to describe the features of trig functions and also prepare the way to look at more complicated trig functions. We will now introduce the definition of two important concepts that help to describe the key features of the functions of sine, cosine and tangent. 1. Period
Trigonometric Equations
Remember to first solve for the trig function and then solve for the angle value. Solution: If there is more than one trig function in the equation, identities are needed to reduce the equation to a single function for solving. Example: Solution: There are trig equations, just like there are normal equations, where factoring does not work!!
Graphing Sine
The amplitude (maximum value) of y = sin x is 1. The period (the time it takes for one full cycle) of y = sinx is 2π. The midline of y = sinx is the x-axis.
Basic Trigonometric Graphs
Trigonometric Functions and Their Graphs: The Sine and Cosine (page 1 of 3) Sections: The sine and cosine, The tangent, The co-functions At first, trig ratios related only to right triangles. Then you learned how to find ratios for any angle, using all four quadrants. Then you learned about the unit circle, in which the value of the hypotenuse was always r = 1 so that sin(θ) = y and cos(θ) = x. In other words, you progressed from geometrical figures to a situation in which there was just one input (one angle measure, instead of three sides and an angle) leading to one output (the value of the trig ratio).
(3) Graphing Trigonometric Functions
Graphs of trigonometric functions look a little crazy at first, especially if you're expecting to find more triangles. They aren't too bad, though, once we get the hang of them. Let's start by looking at a graph of a basic sine function, y = sin x:
Trigonometric Functions and Their Graphs: Tangent
Trigonometric Functions and Their Graphs: The Tangent (page 2 of 3) Sections: The sine and cosine, The tangent, The co-functions The next trig function is the tangent, but that's difficult to show on the unit circle. So let's take a closer look at the sine and cosines graphs, keeping in mind that tan(θ) = sin(θ)/cos(θ). The tangent will be zero wherever its numerator (the sine) is zero.
Graphs of Sine, Cosine and Tangent
Here are some nice graphs to look at ... Plot of Sine The Sine Function has this beautiful up-down curve (which repeats every 2π radians, or 360°). It starts at 0, heads up to 1 by π/2 radians (90°) and then heads down to -1. Plot of Cosine Cosine is just like Sine, but it starts at 1 and heads down until π radians (180°) and then heads up again.