

Archimède de Syracuse. Mécanique newtonienne. Un article de Wikipédia, l'encyclopédie libre.
La mécanique newtonienne est une branche de la physique. Depuis les travaux d'Albert Einstein, elle est souvent qualifiée de mécanique classique. Histoire[modifier | modifier le code] De nombreux mathématiciens y ont apporté une contribution souvent décisive, parmi eux des grands noms tels que Euler, Cauchy, Lagrange... Jusqu'à la fin du XVIIIe siècle, la mécanique a été le domaine applicatif naturel des mathématiques, le domaine dans lequel on pouvait tenter de faire entrer les faits expérimentaux dans le cadre rigoureux des mathématiques.
Courbe balistique parabolique suivant les équations dorénavant acceptées en mécanique classique Au début du XXe siècle, Einstein a développé sa célèbre théorie de la relativité et a mis en évidence les insuffisances de la mécanique telle qu'elle a été décrite par Newton. Conceptuellement, la mécanique a connu trois révolutions : Classification[modifier | modifier le code] Source[modifier | modifier le code] La mécanique de Newton. La mécanique de Newton I.
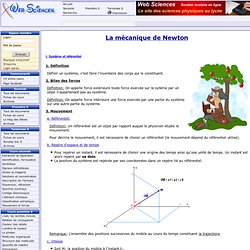
Système et référentiel 1. Définition Définir un système, c'est faire l'inventaire des corps qui le constituent. 2. Définition: On appelle force extérieure toute force exercée sur le sytème par un objet n'appartenant pas au système. Définition: On appelle force intérieure une force exercée par une partie du système sur une autre partie du système. Grossheny.free.fr/pcschwi/pcjbs/ts/phy/Tsphy09.pdf. Physique_11_LA_MECANIQUE_DE_NEWTON. Loi de Newton. I - Vecteurs vitesse et accélération 1) Vecteur vitesse Un vecteur vitesse au point Mi est défini par une relation approchée: Le vecteur a: Point d'application: Mi Direction: tangente au mouvement au point Mi Sens : celui du mouvement A un instant t quelquonque: Dans un repere orthonormé (O,i,j,k) un point M mobile de coordonées x, y et z a pour vecteur position: On a donc: 2) Vecteurs accélération Un vecteur acceleration a un instant ti au point Mi est défini par une relation: Il a pour caractéristiques: II - Lois de newton 1) Principe de l'inertie Dans un référentiel galiléen, un objet soumis à des forces qui se compensent, c'est à dire: Le vecteur vitesse de son centre d'inertie (assimilé en Terminale au centre de gravité) ne varie pas, on a alors:

Cours de mécanique des fluides. 1 - Définition Un fluide peut être considéré comme étant formé d'un grand nombre de particules matérielles, très petites et libres de se déplacer les unes par rapport aux autres.

Un fluide est donc un milieu matériel continu, déformable, sans rigidité et qui peut s'écouler. Parmi les fluides, on fait souvent la distinction entre liquides et gaz. 2 - Liquides et gaz Les liquides et gaz habituellement étudiés sont isotropes, mobiles et visqueux. . · l'isotropie assure que les propriétés sont identiques dans toutes les directions de l'espace. · la mobilité fait qu'ils n'ont pas de forme propre et qu'ils prennent la forme du récipient qui les contient. · la viscosité caractérise le fait que tout changement de forme d’un fluide réel s'accompagne d'une résistance (frottements). 3 - Forces de volume et forces de surface · principe de la conservation de la masse. · principe fondamental de la dynamique. · principe de la conservation de l'énergie. 1.1 - Débit-masse Débit-volume 1.3 - Relation entre qm et qV ou.
La mécanique de Newton : ce qu’il faut en retenir. « La mécanique de Newton » est le premier chapitre de la mécanique.
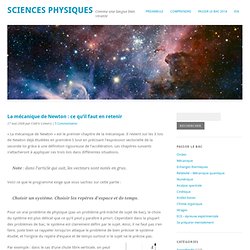
Il revient sur les 3 lois de Newton déjà étudiées en première S tout en précisant l’expression vectorielle de la seconde loi grâce à une définition rigoureuse de l’accélération. Les chapitres suivants s’attacheront à appliquer ces trois lois dans différentes situations. Note : dans l’article qui suit, les vecteurs sont notés en gras. Voici ce que le programme exige que vous sachiez sur cette partie : Choisir un système. Pour un vrai problème de physique (pas un problème pré-mâché de sujet de bac), le choix du système est plus délicat que ce qu’il peut y paraître à priori.
Par exemple : dans le cas d’une chute libre verticale, on peut choisir de prendre comme origine du repère la position du système au moment où il est lâché et comme origine du temps le moment où il est lâché. Animations Flash. Satellites et planètes.