Zoom
Trash

L'Hypothèse de Riemann — Science étonnante #62. Deux (deux ?) minutes pour... l'hypothèse de Riemann. L'incroyable addition 1+2+3+4+...=-1/12 - Micmaths. Bernhard Riemann. Bernhard Riemann Compléments Biographie[modifier | modifier le code] Enfance[modifier | modifier le code] Bernhard Riemann est né à Breselenz, un village du royaume de Hanovre.
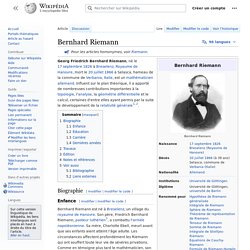
Son père, Friedrich Bernhard Riemann, pasteur luthérien[1], a combattu l'armée napoléonienne. Éducation[modifier | modifier le code] Lorsque Bernhard a dix ans, son père engage un professeur particulier pour qu'il enseigne à son fils la géométrie et l'arithmétique. Carrière[modifier | modifier le code] Sa carrière scientifique ne dura qu'un peu plus de dix ans : elle débute en 1849, lorsqu'il commence sa thèse doctorale, et se termine prématurément au début des années 1860, avec la rédaction de ses derniers articles.
Après avoir soutenu sa thèse d'habilitation en 1854, Riemann prend du repos à Quickborn où il vit toujours avec ses parents, son frère et certaines de ses sœurs. Ken Ono - The Riemann Hypothesis (March 14, 2018) Visualizing the Riemann zeta function and analytic continuation. Riemann's paradox: pi = infinity minus infinity. Biographie de Bernhard Riemann. Bernhard Riemann est né le 17 septembre 1826 à Hanovre.

Son père est pasteur luthérien, et il reçoit à cet égard une éducation rigoureuse et très respectueuse de la famille. Au lycée, il est un élève appliqué et studieux, mais son perfectionnisme excessif l'empêche parfois de rendre ses devoirs en temps voulu. Il est déjà victime de ses problèmes d'expression écrite et orale qui pèseront plus tard sur son activité de recherche, et feront qu'il ne sera pas reconnu, du temps de son vivant, à sa juste valeur. Le père de Riemann consent à ce qu'il aille étudier la théologie à l'université de Göttingen.
Mais Riemann se passionne pour les mathématiques, et avec l'autorisation de son père, il s'inscrit à la faculté de philosophie. Dans la foulée, Riemann prépare son habilitation pour devenir PrivatDozent. Riemann, une hypothèse de premier plan. Dixième volet de la collection « Génies des mathématiques », Bernhard Riemann, dont la contribution influença jusqu’au développement de la cosmologie.
Le Monde | 23.05.2018 à 11h13 • Mis à jour le 23.05.2018 à 15h28 | Par Patrick Popescu-Pampu (Professeur de mathématiques au Laboratoire Paul-Painlevé de l’université de Lille, spécialiste de théorie des singularités) Collection « Génies des mathématiques ». Lorsqu’il s’éteignit à l’âge de 40 ans, en 1866, le mathématicien allemand Bernhard Riemann avait publié seulement six articles. Son œuvre complète, qui les rassemble au côté de textes posthumes, ne totalise même pas 500 pages. Cela semble bien peu, comparé aux dizaines de milliers de pages d’écrits mathématiques d’Euler ou Cauchy. Plusieurs de ces notions remontent aux Eléments d’Euclide. Hypothèse fascinante Y a-t-il un lien entre le plan et les nombres premiers ?
Bernhard Riemann. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Fils de pasteur, voué de par la volonté paternelle à des études théologiques, le jeune Bernhard entre à l'université de Göttingen (1846) afin étudier la philosophie malgré son attrait et ses brillantes capacités pour les mathématiques.

Sa rencontre avec Gauss, mathématicien et astronome réputé, sera déterminante : il sera mathématicien. Gauss, alors âgé de 74 ans, dirigea sa thèse (1851) sur les fonctions d'une variable complexe en la célèbre université de Göttingen. Riemann fut lui-même professeur à Göttingen, succédant à ce dernier en 1859 (Dirichlet avait lui-même succédé à Gauss quatre ans plus tôt).
Riemann mourut prématurément à peine âgé de 40 ans, atteint de tuberculose à Selesca (lac Majeur, Italie) où il se soignait. » Briot , Bouquet , Laurent. Hypothèse de Riemann. Fonctions spéciales La fonction zêta joue un rôle important en recherches mathématiques.

Elle constitue un premier lien entre arithmétique et analyse. Elle a été utilisée par Euler, Dirichlet, Tchebychev et Riemann pour étudier la distribution des nombres premiers. La fonction zêta de Riemann et les fonctions L de Dirichlet sont des outils analytiques puissants pour étudier la répartition des nombres premiers. Il semble que ces fonctions soient aussi révélatrices des propriétés les plus cachées de la théorie des nombres. Elles sont loin d'être bien comprises! En 1737 Leonhard Euler (1707-1783) étudie la fonction zêta et découvre l'identité d'Euler entre les nombres premiers et les nombres entiers. En 1859 Georg Riemann (1826-1866) émet son hypothèse. En 1900 David Hilbert (1862-1943) place l'hypothèse de Riemann parmi les grands défis mathématiques du XXe siècle (n°8).
L'approximation de Riemann par les rectangles. Définition et convergence pour une série de Riemann.