

- Matemáticas - G · Polígonos regulares [Construcción] Publicado en 01.- Geometría plana En esta construcción puedes estudiar los polígonos regulares de 3 a 20 lados.Si mueves los deslizadores [ radio ] y [ lados] obtines los datos de cada uno de los polígonos regulares.Observa que cuanto mayor número de lados el área del polígono se acerca al área del círculoObserva que cuanto mayor número de lados el perímetro del polígono se acerca a la longitud de la circunferencia circunscrita.
![- Matemáticas - G · Polígonos regulares [Construcción]](http://cdn.pearltrees.com/s/pic/th/matematicas-construccion-218835587)
Trazados Geométricos. Cicloides. Trazados Geométricos. Hilo y Papel….Geometria (HILORAMAS) Tarea : usar la mínima cantidad de puntos para crear un patrón.
Este mètodo de trabajo se relaciona con los hilogramas “El hilorama es una técnica que se caracteriza por la utilización de hilos de colores, cuerdas o alambres tensados que se enrollan alrededor de un conjunto de clavos para formar figuras geométricas, abstractas u otros tipos de representaciones. Este procedimiento se suele llevar a cabo sobre una base de madera pintada o tapizada, y con él se puede reproducir cualquier idea imaginable. Generalmente, aunque las figuras están formadas por líneas rectas, los diferentes ángulos y posiciones en el que los hilos se cruzan pueden dar la apariencia de las Curvas de Bézier.
Otras formas de este arte de cuerda incluyen el estilo Spirelli, utilizado normalmente para la realización de tarjetas y álbumes de recortes, entre otras cosas. Sin embargo en este caso hacemos uso de papel y hojas agujereadas, el proceso es sencillo y se puede trabajar en todos los niveles.
Geometric Definitions. Torneo Geodin. ¿En que consiste el Torneo GEODIN?
Torneo Geodin quiere decir: "Torneo de Geometría Dinámica" Se trata de una competencia por equipos para estudiantes de primaria y secundaria. Consiste en resolver problemas de geometría en equipo usando algún software de computadora, que permite la exploración de los enunciados de una forma dinámica. Por ejemplo, modificar una figura al mover un punto sin que se alteren las relaciones geométricas determinadas. Esto permite permite realizar observaciones mediante experimentación y formular conjeturas que luego se tendrán que investigar. Los problemas van desde los más clásicos que se puedan formular de la geometría sintética hasta la preparación de animaciones o simulaciones en las que se apliquen conceptos geométricos.
¿Quiénes participan? Pueden participar todos los estudiantes de niveles primaria y secundaria, en tres niveles de competencia ¿Cuándo son las pruebas? El desarrollo del Torneo consta de dos instancias: ¡Qué bueno! Me encanta esta actividad y las cosas que logran hacer los estudiantes!… Debora Pereiro - Debora Pereiro a partagé une publication. Xeometría plana. Icosaedro. * Inscrición nos outros poliedros regulares No tetraedro catro caras están centradas coas do poliedro circunscrito.

As aristas do icosaedro, prolongadas, cortan os vértices e as seccións áureas das aristas do tetraedro. Nas caras do hexaedro sitúanse seis aristas centradas que son sección áurea das do cubo. No Octaedro cada vértice sitúase na sección áurea dunha arista. No Dodecaedro cada vértice está no centro dunha cara. Os poliedros son duais. Polyèdre chanfreiné. POLYÈDRE TRONQUÉ Truncated polyhedron, abgestumpftes Polyeder Un polyèdre est dit être obtenu par troncature d'un polyèdre de départ s'il est obtenu en ôtant de ce polyèdre (plein) l'intersection avec un demi-espace.

Lorsque la troncature fait disparaître un sommet et des portions d'arêtes aboutissant à ce sommet, on parle de troncature de sommet, détaillée sur cette page. Lorsque la troncature fait disparaître une arête et des portions d'arêtes aboutissant aux extrémités de cette arête, on parle de troncature d'arête. Pour les polyèdres réguliers on distingue 4 types de troncatures conduisant à des polyèdres ayant encore certaines régularités : Octaèdre. Octaèdre. Árbol de Pitágoras. Flexstick- Geodésicas: Juego de construcción. Mapping Our Tiles. Mapping Our Tiles. El icosaedro y su volumen. Un icosaedro es un sólido platónico.
Sus caras son triángulos equiláteros, al igual que el tetraedro y el octaedro. Ya hemos visto varias propiedades del icosaedro y muchas maneras de construirlo. Tiene una belleza especial y, por otro lado, es muy sencillo de construir. Por ejemplo, esta lámpara icosaédrica hecha con cartulina y gomas elásticas: El icosaedro está relacionado con el pentágono y la proporción áurea. Además hemos visto una construcción muy bonita que muestra que los 12 vértices del icosaedro están en tres rectángulos áureos perpendiculares dos a dos. En esta página vamos a calcular el volumen del icosaedro.
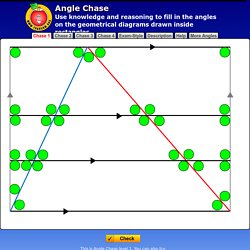
Parece una tarea complicada pero no lo es si sabemos mirar en su interior y aplicamos dos herramientas básicas: 1) El cálculo del volumen de una pirámide pues podemos imaginarnos el icosaedro formado por pirámides cuya base es una cara que es un triángulo equilátero. 2) Necesitamos saber la altura de esas pirámides, es decir la distancia de una cara al centro del poliedro. Pagina nueva 1. TESSELLATION KIT. Angle Chase. Description of Levels Close Level 1 - 31 angles to be found in a diagram with one set of parallel lines Level 2 - 42 angles to be found in a diagram with three sets of parallel lines Level 3 - 69 angles to be found in a fiendishly complex diagram Level 4 - Impossible unless you know the circle angle theorems Answers to this exercise are available lower down this page when you are logged in to your Transum account.
Kite Maths. Introduction Explore Geometry With Kites!

Can you make a kite shape from a single A4 size sheet of paper using only three folds? Click Here to find out how. Will your kite tessellate? Can you put a number of kites together to make a symmetric design? Can you write a procedure in Logo to draw a kite .... what designs can you make with your Logo kites? What is a kite? Areas of Composite Shapes. ÍNDICE.