

Intégration (mathématiques) En mathématiques, l'intégration est le fait de calculer une intégrale.
C'est aussi une des deux branches du calcul infinitésimal, appelée également calcul intégral, l'autre étant le calcul différentiel. Les différents domaines dans lesquels peuvent se rencontrer des intégrales ont conduit à donner des définitions différentes de l'intégrale permettant d'en calculer pour des fonctions de moins en moins régulières. On rencontre ainsi les intégrales dites de Riemann, de Lebesgue ou de Kurzweil-Henstock. Mais toutes ces définitions coïncident dans le cas des fonctions continues. Le symbole mathématique représentant l'intégration, le « S long » : , est appelé signe somme, signe d'intégration, signe intégral ou intégrateur ; il a été introduit par Leibniz pour noter l'intégrale. L'intégrale : introduction. Calcul d'intégrales : la primitive. Calcul d'intégrales : exemples. Calcul intégral : une petite mise au point. Intégrale de Riemann.
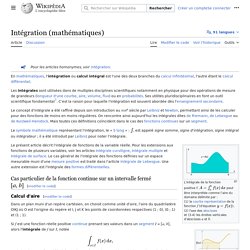
ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges On sait depuis Mercator et Leibniz, que si f est une fonction positive et supposée continue sur un intervalle [a,b], l'intégrale de f sur cet intervalle évalue l'aire sous sa courbe représentative dans un repère du plan.

S'inspirant de l'intégrale de Cauchy, basée sur cette même conception géométrique mise en place en 1821-1823 pour les fonctions continues, Riemann élargit le concept d'intégrale à des fonctions numériques non nécessairement continues mais bornées sur l'intervalle d'étude [a,b] et partout définies sur [a,b] sauf éventuellement en un nombre fini ou dénombrable de points isolés. Les fonctions en escalier : Étant donné un intervalle [a,b] de R, on appelle subdivision de cet intervalle une suite finie (xi) de points de [a,b] : a = xo < x1< x2 < ... < xi < ... < xn= b On appelle pas de la subdivision le plus grand des écarts xi+1- xi. Intégrale de Riemann 1/4 : construction du concept. Introduction à la théorie de la mesure - Lebesgue # 1. Intégrale de Lebesgue. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges L'intégrale de Lebesgue demande une longue introduction théorique relative à la théorie de la mesure (»Jordan , Borel) et apparaît très abstraite.

Construite dans le cas de fonctions numériques, l'intégrale de Lebesgue se situe aujourd'hui dans le cadre de fonctions définies dans un espace topologique localement compact (tout point admet un voisinage compact) à valeurs dans un espace vectoriel réel. Son développement dépasse largement le cadre de cette chronologie. On peut cependant tenter d'en donner un aperçu de la façon suivante en précisant quelques éléments de vocabulaire : Historiquement, avec Riemann principalement, la notion d'intégrale est directement au calcul d'aires : aire "sous" la courbe dans le cas d'une fonction numérique positive.
Soit f une fonction numérique continue de support compact [a,b]. ! » Lusin. PolyIntL3. CompilationLsma320MathChimie2012a15. MA202 Integration. Intégration par changement de variable : l'aire du cercle. Intégrales. Motivation Tout comme nous avons réussi à donner une interprétation graphique à la fonction dérivée (pente de la tangente), nous cherchons ici à donner une interprétation graphique à la notion de primitive.

Cela ne peut se faire de façon satisfaisante qu'au moyen de la notion de 'surface' ou "d'aire" d'une partie du plan. Cela pose d'entrée certains problèmes théoriques du type: "Quelles sont les parties du plan, susceptibles de se voir attribuer une aire? La croyance 'naïve' que toute partie est 'mesurable' se heurte très vite à des difficultés théoriques qui ne sont pas forcément liées à la notion de dimension. On rencontre les mêmes problèmes avec la longueur des courbes et la mesure des volumes dans l'espace. Galerie des portraits Nous suivrons ici les traces de Bernhard Riemann qui a poursuivi le travail de Cauchy dans cette direction et dont la pensée se résume simplement.
Intégration par parties: Principe. Miguel Rodrigues - Comment mesurer la taille d'une fonction ? Intégration. L'intégrale de Riemann complétée est une version améliorée de l'intégrale de Riemann, aussi élémentaire mais bien plus puissante : elle contient l'intégrale de Lebesgue, toutes les intégrales "impropres", elle intègre toutes les dérivées; tous les bons théorèmes (convergence monotone, convergence dominée, Fubini, changement de variable, lien avec les primitives, etc.) s'y appliquent et se démontrent facilement : toutes les preuves sont du niveau des deux premières années de la Licence actuelle.

Ch int. Méthodes d'intégration. PolyUF1 4a. CoursIntegration 2014. 11k. Integration. Ma222_C1.pdf. Integration memo. Leçon Intégration - aires et volumes - Cours maths Terminale. 41 Intégrales : calcul de volume. Calcul d'un volume par intégration séquence 1. Thomaths 4 - Intégrale Curviligne. Thomaths 8 - Intégrales multiples et Formes différentielles. Cours311 2. Licence 2 (Analyse) Séance du 18 mars Fin cours intégrales généralisées et début correction TD3. 4 3 Partie 1. 4 3 Partie 2.
ISf. Produit de convolution. Integration. Surfaces paramétrées et intégrales des surfaces. Intégrales multiples. Intégration aires et volumes. Week by week description. Les différents types de convergence - Les Amphis de France 5. En poursuivant votre navigation, vous acceptez le dépôt de cookies destinés à mesurer la fréquentation du site et pour vous proposer des services adaptés à l’utilisation du site OK | En savoir plus Canal-U Mon compte Accueil > VidéoLes Amphis de France 5 > Mathématiques > Mathématiques - Licence > Les différents types de convergence Les différents types de convergence Volume 90% Press shift question mark to access a list of keyboard shortcuts Raccourci Clavier Play/PauseEspace Augmenter le Volume↑ Diminuer le Volume↓
Les théorèmes de convergence monotone et de convergence dominée de Lebesgue - Les Amphis de France 5. En poursuivant votre navigation, vous acceptez le dépôt de cookies destinés à mesurer la fréquentation du site et pour vous proposer des services adaptés à l’utilisation du site OK | En savoir plus Canal-U Mon compte.
MesureIntegration. Doss 2010 integration probabilites. Introduction à la théorie des distributions. 2015 2016 MACS2 Distributions. Jean Michel Bony Cours d'analyse. Théorie des distributions et analyse de Fourier Ellipses(2001) Théorie ergodique. Théorie de la mesure, ensemble mesurable. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges à 28 ans, dans ses Leçons sur la théorie des fonctions (»ref. 1), Borel, après des considérations préliminaires relatives (Ch. 1 à 3) : aux ensembles infinis, la non dénombrabilité de l'intervalle [0,1] de la droite réelle, la puissance du continu; aux nombres algébriques et transcendants et l'approximation des nombres irrationnels (en particulier au moyen de développements en fraction continue); aux ensembles dérivés et parfaits selon Cantor et relativement parfait selon Jordan (ensembles contenant leur dérivé, ne différant que d'une partie dénombrable); définit la mesure de sous-ensembles de l'intervalle [0,1] de R (Ch. 4, page 46 du livre, page 60 du fichier pdf).

Borel, Émile Félix. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges » Source portrait : avec l'aimable autorisation du Portail de la ville de Saint-Affrique en Aveyron où l'on trouvera une biographie plus complète en cliquant sur l'image.

Éléments biographique : Ibid, + CDSB + Académie des sciences. Né à Saint-Affrique (Aveyron), major de Polytechnique et de l'École Normale Supérieure à 18 ans, sa thèse Sur quelques points de la théorie des fonctions fut dirigée par Darboux (1893). Le concept d'ensemble mesurable, initié par Jordan, sera magistralement développé par Borel (Leçons sur la théorie des fonctions, 1898, »réf.1) et deviendra le fondement de l'analyse mathématique moderne sur lequel s'appuiera Lebesgue pour la mise en place de sa théorie de l'intégrale.
[UT#4] Introduction aux intégrales impropres. Intro cours distribution MACS2. Introduction à la théorie des distributions. [GS#1] Théorie des distributions - Une introduction. Mesure (et théorie de Lebesgue)