

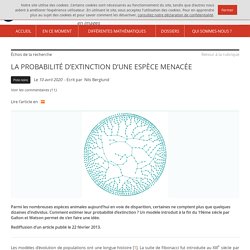
Intro proba 1. Intro proba 2. Intro proba 3. Les probabilités ont la cote ! L’univers Ω renferme ici toute une population, matérialisée par les nombreux points comme autant d’individus la composant, malades ou non, réactifs ou pas.
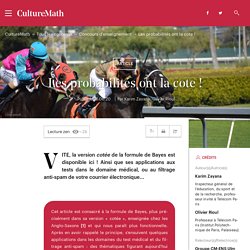
C’est une immense urne dans laquelle on pioche. Par commodité, les catégories qu’elle abrite ont été regroupées sur le dessin, plutôt que dispersées. On jauge ainsi mieux leurs poids relatifs, mais il est convenu qu’un individu sera tiré au sort, à l’aveugle. Les contours de M et de t ne s’épousant pas, ils délimitent quatre régions : les zones externe et interne pour les vrais positifs VP (le sous-ensemble M∩t) et les vrais négatifs VN (correspondant à ¯M∩¯t), et, comme un flou aux interstices, les faux positifs FP (correspondant à ¯M∩t) et les faux négatifs FN (correspondant à M∩¯t).
Ces deux dernières franges trahissent les imperfections du test. Selon son paramétrage, un test peut gagner sur l’un des deux flancs FP ou FN, mais perd automatiquement sur l’autre. Schématiquement, on pourrait distinguer deux situations : 4.5. 4.6. Livres de Probabilités.
PolyProbas. Aléatoire: Introduction aux Probabilités (École Polytechnique) Formulaire de Mathématiques : Mémento sur les probabilités. Propriétés élémentaires On a les propriétés élémentaires suivantes : Probabilité d'une réunion si les événements sont 2 à 2 incompatibles : sinon, on applique la formule du crible : Probabilité d'une intersection si les événements sont indépendants : sinon, on applique la formule des probabilités composées : Soient A1,..., Am m événements tels que .
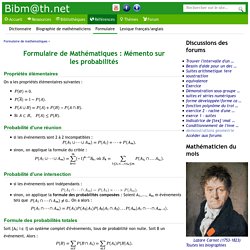
Formule des probabilités totales.
1. Probabilités et variables aléatoires. Introduction aux loix à densité: avec des entiers. OC stat5. OC stat6. Bernoulli Binomiale. Loi binomiale. 2. La Loi Normale. Courbe de Gauss. #4 LOI NORMALE ou LOI DE GAUSS. Statistiques. Chapitre 14 Espaces probabilisés finis. MQD 2 : Variable Aléatoire ? Chapitre 18 Variables aléatoires. Chapitre 22 Couples de variables aléatoires. Ch06Probabilitesconditionnelles papier. Exercice sur les probabilités conditionnelles. Les probabilités conditionnelles et l'indépendance de deux événements (31 mars) - Vidéo Spécialités. Probabilités conditionnelles : de Bayes à Monty Hall. Formule de Bayes et applications (mêmes philosophiques) Hors-Série "Les maths au quotidien" : la paradoxe des anniversaires.
Paradoxe de Monty Hall.
Lois des grands nombres. SC TRIBUS. Théorèmes limites. Quelques demonstrations. Calcul Proba Blaise Pascal HISTOIRE DES MATHS. La vallee poussin analyse. Bibliothèque Tangente HS 17 Hasard Et Probabilités [ HQ] : Free Download, Borrow, and Streaming. Genèse loi Normale. Va reelles. Variable aléatoire continue. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Avec l'apparition de la théorie de la mesure (initiée par Borel), une théorie moderne, voire abstraite, des probabilités s'est développée dans la première moitié du 20è siècle.

Une probabilité sur un ensemble (espace probabilisé) apparaît alors comme une mesure définie dans cet ensemble, et à des fins pratiques portant sur l'usage de l'intégration au sens de cette mesure (fonctions de répartition, densité de probabilité), il est alors fait usage de variables aléatoires absolument continues pour signifier que leurs fonctions de répartition est absolument continue. L'exposé ci-dessous se restreint au cadre "élémentaire" de l'intégrale de Cauchy équivalente à celle de Riemann pour les fonctions continues. Pour un aspect plus théorique, on pourra consulter les liens indiqués in fine (réf. 6 à 10).
Convergences. Cours proba. Cours chap 4. Variable aléatoire. Partie 1. Variable aléatoire. Partie 2. VARIABLE ALÉATOIRE POUR TOUS. VARIABLE ALÉATOIRE DISCRÈTE ET LOI DE PROBABILITÉ. LOI BINOMIALE. Loi de Poisson. LOI DE POISSON EN DCG UE 11. Approximation d'une loi binomiale par une loi de Poisson. VARIANCE D'UNE SOMME DE VARIABLES ALÉATOIRES.
ESPÉRANCE DU PRODUIT DE DEUX VARIABLES ALÉATOIRES INDÉPENDANTES. OPÉRATIONS SUR LES VARIABLES ALÉATOIRES. DCG. DSCG. MASTER. OPÉRATIONS SUR LES VARIABLES ALÉATOIRES PAR L'EXEMPLE EN DCG. OPÉRATIONS SUR LES VARIABLES ALÉATOIRES. DCG UE 11. VARIABLES ALÉATOIRE. CHANGEMENT DE VARIABLE. VARIABLE ALÉATOIRE CONTINUE ET LOI UNIFORME. VARIABLE ALÉATOIRE CONTINUE. LOI NORMALE. APPROXIMATION D'UNE LOI BINOMIALE PAR UNE LOI NORMALE. TEST DU KHI DEUX. Chapitres 8 et 14, probabilités. c1. c2. Densité de probabilité et distance entre deux points. Cproba. Ma121_Cours_1819_CHAP1.pdf. Ma121_Cours_1819_CHAP2.pdf. Cours mktro. Fascicule2 proba 1ere filigranee. Matrices aléatoires. ProbaAvr14.pdf. Alea2014Pouyanne. LES PAPAS Promenades Aléatoires en Paysage Aléatoire.
Les modèles présentés ici sont des modèles probabilistes.
Il sera donc utile de se rappeler qu’une probabilité mesure la chance qu’a un événement de se produire. La probabilité qu’a un événement de se produire est un nombre compris entre (=0%) et (=100%). signifie que l’événement ne se produit jamais. signifie que l’événement se produit toujours. Précisions pour les lecteurs Précisions pour les lecteurs plus avancés dans la théorie des probabilités : on aurait dû ajouter ici le mot « presque » et écrire « presque jamais » au lieu de « jamais » et « presque toujours » au lieu de « toujours ». Marches aléatoires (MA) en dimensions 1 et 2 Considérons un marcheur se déplaçant au hasard sur des sites placés sur une droite et numérotés par .
S’il obtient « 1 ou 2 », il va se placer sur le site situé à droite de sa position, s’il obtient « 3 ou 4 », il va se placer sur le site situé à gauche de sa position, s’il obtient « 5 ou 6 », il ne bouge pas. Ce modèle est une marche aléatoire en dimension 1. Faculté de médecine Sorbonne Université - Biostat. Licence 3 Maths - Intégration et Probabilités. Loading [MathJax]/jax/element/mml/jax.js.
Intro proba 1. Cours de Probabilités n°2 (Fac) Cours de Probabilités n°1 (Fac) Prbdeug2. Cours proba as. Ens Proba stochastiques en temps discret. LA PROBABILITÉ D’EXTINCTION D’UNE ESPÈCE MENACÉE. Les modèles d’évolution de populations ont une longue histoire [1].
La suite de Fibonacci fut introduite au XIII siècle par Léonard de Pise pour décrire la croissance d’une population de lapins. Le modèle le plus connu d’évolution de populations est sans doute celui de Malthus, proposé au début du XIX siècle. Supposons que chaque année, des individus de la population donnent naissance à un enfant, et que meurent. L’augmentation nette sera donc de , ce qui conduit à une croissance exponentielle, comme pour les intérêts composés d’un compte d’épargne [2]. Le modèle de Malthus peut être affiné de diverses manières, par exemple en faisant dépendre le taux de croissance de l’effectif de la population pour tenir compte de la limitation des ressources, ce qui conduit au modèle logistique. Ici, il sera question d’un modèle probabiliste, introduit en 1874 par Francis Galton et Henry William Watson pour décrire l’extinction des noms de famille [GW]. Comment trouver la probabilité d’extinction. Semmelweis. Semmelweis. SHM - 18/12/2015 - Mathématiques et jeux : histoires croisées - Tristan Cazenave.
696 Texte de l'article 2680 1 10 20181106. LES URNES DE POLYA 6. Jean Michel et le théorème de Polya - Math&Magique #6. Michel Henry article pour Mathematice. Proba 06 HenryV C. 06 HenryV C. Extraits textes proba. Deux (deux ?) minutes pour... les nombres de Catalan. Deux (deux ?) minutes pour... Newroz. Desolneux Agnès - "Buffon et le hasard en géométrie" - 2017.
Estimation de pi par le lanceur de fléchettes aveugle. Estimation de pi par les aiguilles de Buffon.