

List of compositions by Wolfgang Amadeus Mozart. This is a selective list of the works of Wolfgang Amadeus Mozart, listed by genre.
The Köchel catalogue contains a complete, chronologically ordered, list. W. A. Mozart Symphony no. 1 in E flat Major - Molto Allegro. Wolfgang Amadeus Mozart. He composed over 600 works, many acknowledged as pinnacles of symphonic, concertante, chamber, operatic, and choral music.
He is among the most enduringly popular of classical composers, and his influence on subsequent Western art music is profound; Beethoven composed his own early works in the shadow of Mozart, and Joseph Haydn wrote that "posterity will not see such a talent again in 100 years. "[3] Early life Family and childhood.
Off-color humor. Toilet humor, or scatological humor, is a type of off-color humor dealing with defecation, urination, and flatulence, and to a lesser extent vomiting and other body functions.
It sees substantial crossover with sexual humor, such as penis jokes. Toilet humor is popular among a wide range of ages, but is especially popular with children and teenagers, for whom cultural taboos related to acknowledgement of waste excretion still have a degree of novelty. The humor comes from the rejection of such taboos, and is a part of modern culture.[1] Examples can also be found in earlier literature, including The Canterbury Tales by Geoffrey Chaucer. Song[edit] How Did the Universe Begin: Hot Big Bang or Slow Thaw? - Communications and Marketing - Heidelberg University. Press Release No. 38/2014 25 February 2014 Heidelberg physicist develops a new theoretical model in which the Big Bang stretches into the infinite past ESA and the Planck Collaboration (Copyright)

1401.5313v1. Scalar field. A scalar field such as temperature or pressure, where intensity of the field is graphically represented by different hues of color.
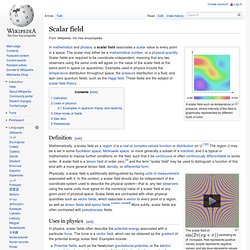
Definition[edit] The scalar field of oscillating as increases. Red represents positive values, purple represents negative values, and sky blue represents values close to zero. Scalar (mathematics) A scalar product operation (not to be confused with scalar multiplication) may be defined on a vector space, allowing two vectors to be multiplied to produce a scalar.
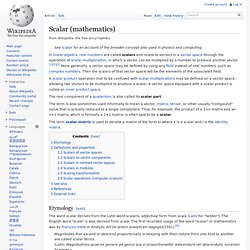
A vector space equipped with a scalar product is called an inner product space. The real component of a quaternion is also called its scalar part. The term scalar matrix is used to denote a matrix of the form kI where k is a scalar and I is the identity matrix. The word scalar derives from the Latin word scalaris, adjectival form from scala (Latin for "ladder"). The English word "scale" is also derived from scala. Magnitudes that ascend or descend proportionally in keeping with their nature from one kind to another are called scalar terms. (Latin: Magnitudines quae ex genere ad genus sua vi proportionaliter adscendunt vel descendunt, vocentur Scalares.) According to a citation in the Oxford English Dictionary the first recorded usage of the term in English was by W. Yields. Quaternion. Graphical representation of quaternion units product as 90°-rotation in 4D-space, ij = k, ji = −k, ij = −ji History[edit] Quaternion plaque on Brougham (Broom) Bridge, Dublin, which says: Here as he walked by on the 16th of October 1843 Sir William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplicationi2 = j2 = k2 = ijk = −1 & cut it on a stone of this bridge Quaternion algebra was introduced by Hamilton in 1843.[7] Important precursors to this work included Euler's four-square identity (1748) and Olinde Rodrigues' parameterization of general rotations by four parameters (1840), but neither of these writers treated the four-parameter rotations as an algebra.[8][9] Carl Friedrich Gauss had also discovered quaternions in 1819, but this work was not published until 1900.[10][11] i2 = j2 = k2 = ijk = −1, into the stone of Brougham Bridge as he paused on it.
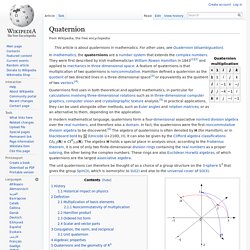
On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Quaternion. Related Topics: Euler's Equation Quaternion is a geometrical operator to represent the relationship (relative length and relative orientation) between two vectors in 3D space.

William Hamilton invented Quaternion and completed the calculus of Quaternions to generalize complex numbers in 4 dimension (one real part and 3 imaginary numbers). Commutative property. Common uses[edit] Propositional logic[edit] Rule of replacement[edit] In standard truth-functional propositional logic, commutation,[1][2] or commutativity[3] refer to two valid rules of replacement.
The rules allow one to transpose propositional variables within logical expressions in logical proofs. The rules are: and where " Commutative, Associative and Distributive Laws. Wow!

What a mouthful of words! But the ideas are simple. Commutative Laws The "Commutative Laws" say we can swap numbers over and still get the same answer ... ... when we add: Example: ... or when we multiply: Isomorphism. The group of fifth roots of unity under multiplication is isomorphic to the group of rotations of the pentagon under composition. In mathematics, an isomorphism, from the Greek: ἴσος isos "equal", and μορφή morphe "shape", is a homomorphism (or more generally a morphism) that admits an inverse. [note 1] Two mathematical objects are isomorphic if an isomorphism exists between them. An automorphism is an isomorphism whose source and target coincide.
The interest of isomorphisms lies in the fact that two isomorphic objects cannot be distinguished by using only the properties used to define morphisms; thus isomorphic objects may be considered the same as long as one considers only these properties and their consequences. Morphism. In category theory, morphism is a broadly similar idea, but somewhat more abstract: the mathematical objects involved need not be sets, and the relationship between them may be something more general than a map. The study of morphisms and of the structures (called objects) over which they are defined, is central to category theory. Much of the terminology of morphisms, as well as the intuition underlying them, comes from concrete categories, where the objects are simply sets with some additional structure, and morphisms are structure-preserving functions.
In category theory, morphisms are sometimes also called arrows. Definition[edit] There are two operations which are defined on every morphism, the domain (or source) and the codomain (or target). If a morphism f has domain X and codomain Y, we write f : X → Y. Category theory. A category with objects X, Y, Z and morphisms f, g, g ∘ f, and three identity morphisms (not shown) 1X, 1Y and 1Z.
Several terms used in category theory, including the term "morphism", differ from their uses within mathematics itself. In category theory, a "morphism" obeys a set of conditions specific to category theory itself. Thus, care must be taken to understand the context in which statements are made. Differentiable function. A differentiable function Differentiable functions can be locally approximated by linear functions.
Vertical tangent. Vertical tangent on the function ƒ(x) at x=c. Limit definition[edit] A function ƒ has a vertical tangent at x = a if the difference quotient used to define the derivative has infinite limit: The first case corresponds to an upward-sloping vertical tangent, and the second case to a downward-sloping vertical tangent. Lines. Slow, cold start to universe suggested. The universe may have emerged not with a hot Big Bang but with a long, cold slog, a physicist proposes in a paper posted online January 21 at arXiv.org. Over the last half-century, most cosmologists have come to agree that all matter initially exploded from a single point. Cosmologist claims Universe may not be expanding. The conventional model of cosmology is that most galaxies recede from one another as space itself inflates like the surface of a balloon — which would explain why other galaxies appear redshifted from our own galaxy's point of view.
Blurring and Unblurring. Spatial frequencies.