

Surface. Index de courbes & fonctions remarquables. Voulez-vous tracer une courbe y = f(x) "on line" ?

Site de G. Valance, professeur de mathématiques. Télécharger un logiciel de tracés de courbes cartésiennes, paramétrique ou polaires : logiciels de Denis Monasse; rubrique Logiciels Courbe2. » Le cas cartésien y = f(x) sera obtenu en choisissant paramétrique en fournissant x = t et y = f(t). Les pseudo-ronds. Ma preuve préférée - AuDiMath. Le triangle de Reuleaux. Vous-êtes vous déjà demandé pourquoi les bouches d’égout sont rondes?
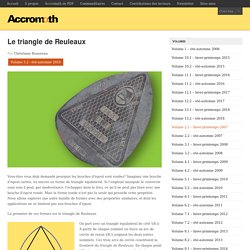
Imaginez une bouche d’égout carrée, ou encore en forme de triangle équilatéral. Si l’employé manipule le couvercle sans soin il peut, par inadvertance, l’échapper dans le trou, ce qu’il ne peut pas faire avec une bouche d’égout ronde. Mais la forme ronde n’est pas la seule qui possède cette propriété. Nous allons explorer une autre famille de formes avec des propriétés similaires, et dont les applications ne se limitent pas aux bouches d’égout. La première de ces formes est le triangle de Reuleaux. On part avec un triangle équilatéral de côté \(R.\) À partir de chaque sommet on trace un arc de cercle de rayon \(R,\) joignant les deux autres sommets.
C’est pour cela qu’on dit que le triangle de Reuleaux a une largeur constante. Mais cela suffit-il à assurer que le triangle de Reuleaux, lorsqu’on le manipule dans l’espace, ne puisse passer au travers d’un trou horizontal d’un rayon \(r < R \! Nous allons voir que oui. Virer sans déraper. Découvrez la clothoïde, aussi appelée spirale de Cornu, la courbe idéale pour éviter les dérapages… Notre intuition nous joue des tours Si on vous demandait de concevoir un tracé pour une voie ferrée reliant deux villes, il y a fort à parier que vous choisiriez de faire un tracé aussi droit que possible et, s’il devait y avoir des tournants, ceux-ci seraient des arcs de cercle, en évitant bien sûr de tracer des tournants trop serrés.
Pour un tracé de route, vous auriez sans doute une approche semblable. Un trajet difficile Est-ce bien ainsi que sont dessinées les vraies voies de chemin de fer et, en particulier, est-ce que les tournants sont bien des arcs de cercle? La courbure On peut tracer un cercle tangent à une courbe en un point P si la courbe est suffisamment régulière en ce point. Cercle osculateur de la courbe au point P La courbure en P est l’inverse du rayon du cercle osculateur, aussi appelé rayon de courbure. Accélération et courbure. Les coniques, une grande famille. Pourquoi met-on dans la même famille des courbes aussi différentes que les ellipses, les paraboles et les hyperboles?
Une première réponse est que ce sont des courbes obtenues comme section d’un cône par un plan. Mais les liens familiaux entre ces courbes sont bien plus forts que cela. Par exemple, toutes ces courbes sont solutions du problème de Kepler : si une planète a une vitesse suffisante, alors elle parcourra plutôt une hyperbole ou encore une parabole avec le Soleil à un foyer. Mais encore… Un argument en apparence farfelu pour lier les différentes coniques serait qu’une parabole est une ellipse qui accroche l’infini, et qu’une hyperbole est une ellipse qui a dépassé l’infini, si bien qu’un morceau est passé de l’autre côté… Essayons de faire un dessin en nous inspirant d’un modèle. Prenons maintenant une ellipse de foyers en F1=(0,0)F1=(0,0) et F2=(b,0)F2=(b,0) où b>0.b>0. Continuons à étirer notre ellipse. En fait, cet argument n’est pas si farfelu. L’équation du second degré : illustration. S e9rie 3 5 Paraboles.
S e9rie 5 6 Quelques belles courbes. Réfléchir sur une parabole. La cycloide. Pourquoi y a-t-il un coeur dans mon bol ? Mathématiques de la tasse de thé. Les phénomènes optiques fascinaient déjà les philosophes de l’Antiquité.

Leur étude est le domaine le plus ancien des sciences physiques. Certains chercheurs en ont fait leur tasse de thé. Lorsque la lumière du Soleil se réfléchit sur le bord d’une tasse de thé, elle forme à la surface du liquide une courbe. Quelle est cette courbe et pourquoi en est-il ainsi ? On sait que les rayons lumineux sont réfléchis de telle sorte que l’angle de réflexion est égal à l’angle d’incidence formé avec la normale à la courbe.
La tasse agit comme un miroir cylindrique. Une courbe formée par la réflexion des rayons lumineux sur une surface ou par la réfraction des rayons lumineux traversant un milieu transparent est appelée caustique qui vient du latin « causticus » et du grec « kaustikos » qui signifie « qui brûle ». Lorsque les rayons lumineux sont issus d’une source à une distance infinie, les rayons lumineux sont parallèles, on a une caustique au Soleil. Néphroïde et tasse de thé Caustique au flambeau. Surfaces minimales. Les bulles de savon.