

[QP#2] Structures algrébriques. Structures algébriques usuelles. INTRODUCTION À L'ALGÈBRE.
Courses – François Bergeron, Mathématiques, UQAM. Accueil. Maths. Deux (deux ?) minutes pour Futurama. Structures algébriques. Structures algébriques Mickaël Launay et Maths Adultes. Cours Structures Algébriques : Groupes Anneaux Corps. Histoire de la théorie des groupes — Wikipédia. Early 19th century[edit] The earliest study of groups as such probably goes back to the work of Lagrange in the late 18th century.
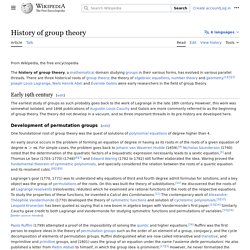
However, this work was somewhat isolated, and 1846 publications of Augustin Louis Cauchy and Galois are more commonly referred to as the beginning of group theory. The theory did not develop in a vacuum, and so three important threads in its pre-history are developed here. Development of permutation groups[edit] One foundational root of group theory was the quest of solutions of polynomial equations of degree higher than 4. An early source occurs in the problem of forming an equation of degree m having as its roots m of the roots of a given equation of degree. Structure de groupe. Groupe (mathématiques) En mathématiques, un groupe est une des structures algébriques fondamentales de l'algèbre générale. C'est un ensemble muni d'une loi de composition interne associative admettant un élément neutre et, pour chaque élément de l'ensemble, un élément symétrique. La structure de groupe est commune à de nombreux ensembles de nombres — par exemple les nombres entiers relatifs, munis de la loi d'addition.
Mais cette structure se retrouve aussi dans de nombreux autres domaines, notamment en algèbre, ce qui en fait une notion centrale des mathématiques modernes. Théorie des groupes. Un article de Wikipédia, l'encyclopédie libre.
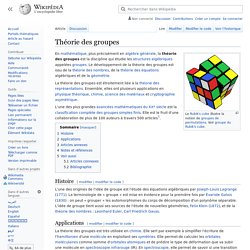
La théorie des groupes est étroitement liée à la théorie des représentations. Ensemble, elles ont plusieurs applications en physique théorique, chimie, science des matériaux et cryptographie asymétrique. Introduction à la théorie des Groupes 2021 (François Bergeron) Cours: Théorie des groupes – François Bergeron, Mathématiques, UQAM. 1) Syllabus, session hiver 20212) Notes de cours: Introduction à la théorie des groupes, (Version 4 octobre 2021, avec de multiples liens dynamiques et illustrations.) 3) Outils pertinents Notes et liens pour: Latex: le principal outil pour l’écriture des mathématiques.Outils de calcul formel: Un logiciel libre spécialisé pour les groupes: Group ExplorerSage: un logiciel libre très général (en cours de construction par une large communauté internationale), qui est parfois un peu plus difficile d’utilisation.
Il inclut des outils pour les groupes. Résumé de cours sur les groupes. THÉORÈME DE LAGRANGE & ORDRE D'UN ÉLÉMENT DANS UN GROUPE. Sous-groupes de R. L'alternative dense/monogène par Caroline. Théorie des anneaux - MacTutor Histoire des mathématiques. Any book on Abstract Algebra will contain the definition of a ring.

It will define a ring to be a set with two operations, called addition and multiplication, satisfying a collection of axioms. These axioms require addition to satisfy the axioms for an abelian group while multiplication is associative and the two operations are connected by the distributive laws. A ring is therefore a setting for generalising integer arithmetic. Familiar examples of rings such as the real numbers, the complex numbers, the rational numbers, the integers, the even integers, 2 × 2 real matrices, the integers modulo m for a fixed integer m, will almost certainly be given in the Abstract Algebra book as will many beautiful theorems on rings but what will be missing are the reasons systems satisfying these particular axioms have been singled out for such intensive study.
What motivated this abstract definition of a ring? The equation xn+yn=zn has no solution for positive integers x,y,z when n>2. Théorie des anneaux. En mathématiques, la théorie des anneaux porte sur l'étude de structures algébriques qui imitent et étendent les entiers relatifs, appelées anneaux.
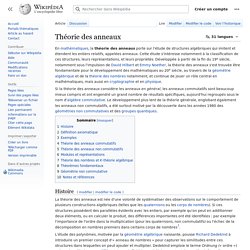
Cette étude s'intéresse notamment à la classification de ces structures, leurs représentations, et leurs propriétés. Développée à partir de la fin du 19e siècle, notamment sous l'impulsion de David Hilbert et Emmy Noether, la théorie des anneaux s'est trouvée être fondamentale pour le développement des mathématiques au 20e siècle, au travers de la géométrie algébrique et de la théorie des nombres notamment, et continue de jouer un rôle central en mathématiques, mais aussi en cryptographie et en physique. Si la théorie des anneaux considère les anneaux en général, les anneaux commutatifs sont beaucoup mieux compris et ont engendré un grand nombre de résultats spécifiques, aujourd'hui regroupés sous le nom d'algèbre commutative. Histoire[modifier | modifier le code] Définition axiomatique[modifier | modifier le code] tel que.
Théorie des Anneaux (François Bergeron) Arithmétique modulaire. En mathématiques et plus précisément en théorie algébrique des nombres, l’arithmétique modulaire est un ensemble de méthodes permettant la résolution de problèmes sur les nombres entiers.
Ces méthodes dérivent de l’étude du reste obtenu par une division euclidienne. L'idée de base de l'arithmétique modulaire est de travailler non sur les nombres eux-mêmes, mais sur les restes de leur division par quelque chose. Quand on fait par exemple une preuve par neuf à l'école primaire, on effectue un peu d'arithmétique modulaire sans le savoir : le diviseur est alors le nombre 9.
Si ses origines remontent à l’Antiquité, les historiens associent généralement sa naissance à l’année 1801, date de la publication du livre Disquisitiones arithmeticae[1] de Carl Friedrich Gauss. Sa nouvelle approche permet d’élucider de célèbres conjectures[2] et simplifie les démonstrations d’importants résultats[3] par une plus grande abstraction. NQRC. Présentation et construction de l'anneau des polynômes à coefficients dans un corps.
Arithmétique dans K[X]
Livres d'Algèbre. ALGÈBRE DE BOOLE. PROPRIÉTÉS. Introduction à l'algèbre booléenne. Cours2007Lsma101. Cours2010Lsma211. Cours2006Msma110. CDD 2 J.Robinet la genèse du calcul algébrique. Ecriture symbolique de l' Algèbre élémentaire. ALGÈBRE 1 ECOLE NORMALE SUPÉRIEURE. ALGÈBRE 2 ÉCOLE NORMALE SUPÉRIEURE 2012–2013. Cours d'algèbre et matrices pour les agrégatifs de l'ENS Lyon session 2020. Cette page regroupe la liste des cours et exercices de révisions d'algèbre donnés à l'ENS Lyon en 2019-2020 dans le cadre de la préparation à l'agrégation.

Si vous consultez occasionnellement, ou régulièrement, ces documents, je vous invite à m'informer par email à l'adresse benoit.loisel[at]ens-lyon.fr : de l'utilité que présentent pour vous ces documents (en tant qu'enseignant pour préparer vos cours, en tant qu'étudiant lors de votre préparation, etc...) ; des différentes erreurs (mathématiques, fautes de frappe, d'orthographe, de grammaire, de syntaxe) que vous auriez constatées afin que je les corrige ; de toute suggestion d'amélioration sur le fond comme sur la forme ; des exemples, applications, exercices que vous auriez aimé voir apparaître dans le cours ou les fiches d'exercices ; de toute autre information qui vous semblerait pertinente.
Cours d'algèbre pour les agrégatifs de l'ENS Lyon session 2019. Cette page regroupe la liste des cours et exercices de révisions d'algèbre donnés à l'ENS Lyon en 2018-2019 dans le cadre de la préparation à l'agrégation.

Si vous consultez occasionnellement, ou régulièrement, ces documents, je vous invite à m'informer par email à l'adresse benoit.loisel[at]ens-lyon.fr : de l'utilité que présentent pour vous ces documents (en tant qu'enseignant pour préparer vos cours, en tant qu'étudiant lors de votre préparation, etc...) ; des différentes erreurs (mathématiques, fautes de frappe, d'orthographe, de grammaire, de syntaxe) que vous auriez constatées afin que je les corrige ; de toute suggestion d'amélioration sur le fond comme sur la forme ; des exemples, applications, exercices que vous auriez aimé voir apparaître dans le cours ou les fiches d'exercices ; de toute autre information qui vous semblerait pertinente. Rennes. Pour chercher et approfondir - A propos de l’antisymétrie.
Groupes et dénombrements. Deux (deux ?) minutes pour John Conway. UN CONCEPT MATHÉMATIQUE, TROIS NOTIONS : LES GROUPES AU XIXE SIÈCLE CHEZ GALOIS, CAYLEY, DEDEKIND. LA TICMATÉMA OU LA MATHÉMATIQUE DU VERLAN. Un exemple pour commencer Voici un tableau de 3 lignes et 3 colonnes.

Amusons-nous à permuter ses éléments en faisant glisser les lignes ou les colonnes. Par exemple, notons l’opération qui consiste à faire glisser la deuxième ligne vers la droite et à ramener le dernier élément en première position. Le tableau suivant montre le résultat de cette opération. Alors que le tableau ci-dessous correspond au glissement d’une unité vers le bas de la première colonne, notons cette opération. Sous-groupe normal. Un article de Wikipédia, l'encyclopédie libre. Définition[modifier | modifier le code] On dit qu'un sous-groupe d'un groupe est normal (ou distingué ou invariant) dans. Catégorie:Action de groupes.
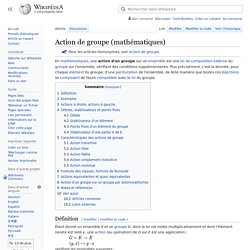
Action de groupe (mathématiques) , une action (ou opération) de G sur E est une application :
Groupe dérivé. Un article de Wikipédia, l'encyclopédie libre. Le procédé d'abélianisation permet souvent de prouver que deux groupes ne sont pas isomorphes. Il intervient aussi en géométrie. Commutateurs[modifier | modifier le code] Liste des petits groupes. Un article de Wikipédia, l'encyclopédie libre. Terminologie et notations[modifier | modifier le code] Zn : le groupe cyclique d'ordre n (parfois noté Cn, il est isomorphe à Z/nZ).D2n : le groupe diédral d'ordre 2n.Sn : le groupe symétrique de degré n, contenant les n!
Permutations de n objets.An : le groupe alterné de degré n, contenant les n! Quelques propriétés de certains groupes finis. Thm Chevalley sur les invariants d'un groupe fini. Théorème de Feit-Thompson. Un article de Wikipédia, l'encyclopédie libre. Historique[modifier | modifier le code] Le théorème lui-même et bon nombre de techniques que Feit et Thompson inauguraient dans leur démonstration jouèrent un rôle essentiel dans la classification des groupes simples finis. La démonstration originale de Feit et Thompson, longue de plus de deux cent cinquante pages, a été simplifiée dans certains détails, mais elle n'a pas été considérablement raccourcie et sa structure générale n'a pas été modifiée. 1OS Groupes. Groupes. Groupes. Anneaux. Idéal. En mathématiques, et plus particulièrement en algèbre, un idéal est un sous-ensemble remarquable d'un anneau : c'est un sous-groupe du groupe additif de l'anneau et qui est de plus stable par multiplication par les éléments de l'anneau.
À certains égards, les idéaux s'apparentent donc aux sous-espaces vectoriels — qui sont des sous-groupes additifs stables par une multiplication externe ; à d'autres égards, ils se comportent comme les sous-groupes distingués — ce sont des sous-groupes additifs à partir desquels on peut construire une structure d'anneau quotient.
En algèbre commutative, deux types d'idéaux sont omniprésents : les idéaux maximaux et, sans doute encore davantage, les idéaux premiers. Quelque idéaux particuliers. Ce site utilise des cookies pour faciliter votre navigation, obtenir des statistiques de visite, et afficher des publicités personnalisées. L3AlgChap3. ATG05ch3. Conséquences algébriques, appartenance aux idéaux et bases de Gröbner. Corps. Structures algébriques 1 : L.C.I. et Groupes. Savant Mélange : Claire Voisin - La notion de groupe : de la géométrie à l'algèbre. SOUS-GROUPES DISTINGUÉS. GROUPE QUOTIENT. ACTION DE GROUPES : DÉFINITIONS ET EXEMPLES. ACTION DE GROUPES 2 : ORBITES ET STABILISATEURS.
Jesua Epequin. Relation d'équivalence, ensembles quotients. Cours MA610. Algebre commutative. MOOC ENS MATHÉMATIQUES ► Introduction à la théorie de Galois. Cours de Théorie de Galois (ens) Tresse (mathématiques) Accueil. Algèbre et Arithmétique. Livre algebre 1. Monoïde. Préambule[modifier | modifier le code] ALGEBRE GROUPES ET ANNEAUX 1 MAFIADOC. Structures algebriques I. Groupes Finis par Jean-Pierre Serre. M1Alg Groupes. Groupes2. Action de groupe (mathématiques) , une action (ou opération) de G sur E est une application : vérifiant les propriétés suivantes : Neverendingbooks. Abeliens2. RappelCorps finis.
M1Alg Modules1. M1Alg Modules2. Algebre. Cours galois 2012. Exogalois. Promenade en théorie de Galois DEA.
Algèbre Géométrique et Informatique Graphique Laurent Fuchs. Implantation des opérateurs de l’algèbre géométrique par arbres binaires récursifs Stéphane Breuils, Vincent Nozick et Laurent Fuchs. Bernard Le Stum - Perfectoïdes.