

Le Jeu de la Vie — Science étonnante #49. Deux (deux ?) minutes pour John Conway. Deux (deux ?) minutes pour la suite de Conway. Une énigme de 50 ans résolue : le nœud de Conway n'est pas bordant - Micmaths. Le jeu de la vie de ConWay : excursion dans des mondes en damiers. Le jeu de la vie de Conway John von Neumann, mathématicien de génie (un des principaux artisans de la réalisation des ordinateurs), se posa il y a une quarantaine d'années la question de l'autoreproduction des machines.

Il créa sur papier un AUTOMATE CELLULAIRE. Ce dernier est constitué d'un damier sur lequel des pions vivent et meurent selon des règles logiques dépendant de leur voisinage. La théorie des automates cellulaires s'est ensuite rapidement développée et suscita un engouement considérable. Le mathématicien américain John Conway a alors imaginé vers 1970 un jeu, appelé "Jeu de la vie" qui met en scèce des cellules susceptibles de se reproduire, de disparaître ou de survivre lorsqu'elles obéissent à des règles quelquefois appelées 'génétiques'. Ces cellules sont représentées ici par des cases sur un quadrillage.
John Horton Conway. Pour les articles homonymes, voir Conway.
John Horton Conway en 2005. John Horton Conway, né le 26 décembre 1937 à Liverpool, est un mathématicien britannique. Extrêmement prolifique, il s'est penché sur les théories des groupes finis, des nœuds, des nombres, des jeux et du codage. Il est professeur émérite de mathématiques à l'université de Princeton. Biographie[modifier | modifier le code] Il obtient son doctorat en 1964, puis un poste à l'université de Cambridge. En 1981, il devient membre de la Royal Society. Conway quitte Cambridge en 1986 pour prendre en charge la chaire John von Neumann de mathématiques à l'université de Princeton. En 2014, il accorde une série d'entretiens filmés au réalisateur Brady Haran (en) pour la chaîne YouTube Numberphile dédiée aux mathématiques. Réalisations[modifier | modifier le code] Théorie des jeux combinatoires[modifier | modifier le code] Géométrie[modifier | modifier le code] Au milieu des années 1960, avec Michael J.
Le cercle de Conway. John Horton Conway. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Élève brillant, John Conway se passionna dès son enfance pour le calcul et la magie des nombres, en un mot : l'arithmétique.

Étudiant à Cambridge, il se spécialisa en théorie des nombres sous la houlette de Davenport qui dirigea sa thèse et fut maître de conférence à l'université de Cambridge (1964) puis professeur (1983). Conway enseigna ensuite à l'université de Princeton. Sémillant pédagogue et vulgarisateur des mathématiques, Conway a publié -souvent en collaboration avec son complice Richard K. Guy, professeur à Calgary, Canada- de nombreux livres destinés à tous les publics. Cherchant à résoudre un difficile problème dans un groupe de symétries d'un espace abstrait, Conway se trouve confronté aux groupes sporadiques et découvre (1968) l'un des trois qui porte désormais son nom. Nombre de chiffres dans la suite de Conway - Maths Otak'
25 avril 2011 1 25 /04 /avril /2011 12:00 Précédemment : Voici les 12 premiers termes de la suite de Conway : On peut émettre la conjecture suivante : Le nombre de chiffre ne diminue jamais quand on passe au terme suivant.
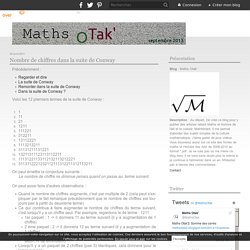
On peut aussi faire d'autres observations : Quand le nombre de chiffres augmente, c'est par multiple de 2 (cela peut s'expliquer par le fait remarqué précédemment que le nombre de chiffres est toujours pair à partir du deuxième terme) Ce qui contribue à faire augmenter le nombre de chiffres du terme suivant, c'est lorsqu'il y a un chiffre seul. Donc deux nombres consécutifs (et non 3) identiques n'ont pas d'influence sur le nombre de chiffre du terme qui arrive juste après Lorsqu'il y a un paquet de 3 chiffres : cela contribue à une diminution du nombre de chiffres 333 donnera 33 222 donnera 32 111 donnera 31 Les seuls chiffres apparaissant dans la suite de Conway semblent être 1,2 et 3. Démonstration :Je vais essayer de procéder à une peuve par récurence. Life, Death and the Monster - Numberphile. Does John Conway hate his Game of Life? The Brain of John Conway (and his Amazing Tongue) - Numberphile.