

Embedding _(mathematics meaning) Googol. The term was coined in 1938[1] by 9-year-old Milton Sirotta, nephew of American mathematician Edward Kasner.
Kasner popularized the concept in his 1940 book Mathematics and the Imagination. Other names for googol include ten duotrigintillion on the short scale, ten thousand sexdecillion on the long scale, or ten sexdecilliard on the Peletier long scale. A googol has no particular significance in mathematics, but is useful when comparing with other very large quantities such as the number of subatomic particles in the visible universe or the number of hypothetical possibilities in a chess game. Edward Kasner used it to illustrate the difference between an unimaginably large number and infinity, and in this role it is sometimes used in teaching mathematics.
A googol is approximately 70! See also[edit] Googol. Da Wikipedia, l'enciclopedia libera.
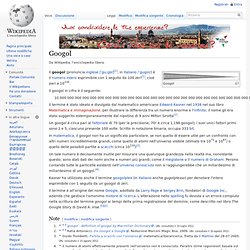
Googol Il googol (pronuncia inglese [ˈɡuːɡɒl][1], in italiano /ˈgugol/) è il numero intero esprimibile con 1 seguito da 100 zeri[1], cioè pari a 10100. Il googol in cifre è il seguente: In matematica, il googol non ha un significato particolare, se non quello di essere utile per un confronto con altri numeri incredibilmente grandi, come quello di atomi nell'universo visibile (stimato tra 1072 e 1087) o quello delle possibili partite a scacchi (circa 10120)[3]. Un tale numero è decisamente inutile per misurare una qualunque grandezza nella realtà ma, nonostante questo, sono stati dati dei nomi anche a numeri più grandi, come il megistone o il numero di Graham. Kasner ha utilizzato anche il termine googolplex (in italiano anche gugolplesso) per denotare l'intero esprimibile con 1 seguito da un googol di zeri. Note[modifica | modifica sorgente] ^ a b googol - definition of googol by Macmillan Dictionary.
Voci correlate[modifica | modifica sorgente] Googolplex. Number ten to the power of a googol A googolplex is the number 10googol, or equivalently, 10(10100).
Written out in ordinary decimal notation, it is 1 followed by 10100 zeroes; that is, a 1 followed by a googol zeroes. History[edit] In 1920, Edward Kasner's nine-year-old nephew, Milton Sirotta, coined the term googol, which is 10100, and then proposed the further term googolplex to be "one, followed by writing zeroes until you get tired".[1] Kasner decided to adopt a more formal definition because "different people get tired at different times and it would never do to have Carnera a better mathematician than Dr. Einstein, simply because he had more endurance and could write for longer".[2] It thus became standardized to 10(10100). Rompicapo. Algebra di Boole. Da Wikipedia, l'enciclopedia libera.
In matematica, informatica ed elettronica, l'algebra di Boole, anche detta algebra booleana o reticolo booleano, è un'algebra astratta che opera essenzialmente con i soli valori di verità 0 e 1. In una formulazione più generale, l'algebra booleana si fonda su un insieme K che non comprende solo i valori 0 e 1; tuttavia questa struttura algebrica nasce per elaborare matematicamente espressioni nell'ambito della logica proposizionale Definizione formale[modifica | modifica sorgente] Si vuole introdurre l'algebra di Boole considerandola come reticolo.
Si parla di algebra di Boole in riferimento a un insieme K sul quale sono definite le operazioni di somma logica (+, OR) e prodotto logico (*,AND), cioè una tripla (K,+,*), che costituisce un reticolo in cui sono inoltre soddisfatte la proprietà distributiva, l'esistenza del minimo e del massimo e l'esistenza del complemento. Nel dettaglio si ha un'algebra di Boole quando su Commutativa Associativa Idempotenza Se e. Apprendere l' informatica. Logica proposizionale. Da Wikipedia, l'enciclopedia libera.
La logica proposizionale (o enunciativa) è un linguaggio formale con una semplice struttura sintattica, basata fondamentalmente su proposizioni elementari (atomi) e su connettivi logici di tipo vero-funzionale, che restituiscono il valore di verità di una proposizione in base al valore di verità delle proposizioni connesse (solitamente noti come AND, OR, NOT...). La semantica della logica proposizionale definisce il significato dei simboli e di qualsiasi proposizione che rispetti le regole sintattiche del linguaggio, basandosi sui valori di verità associati agli atomi. Data una interpretazione (o modello) di una proposizione (in generale di un insieme di proposizioni), e cioè una associazione tra le proposizioni elementari e le realtà rappresentate, possiamo generare un insieme infinito di proposizioni con significato definito che riguardino quella realtà.
Sintassi[modifica | modifica sorgente] Alfabeto[modifica | modifica sorgente] Inclusione. Da Wikipedia, l'enciclopedia libera.
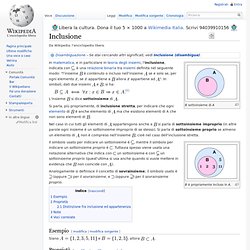
B sottoinsieme di A In matematica, e in particolare in teoria degli insiemi, l'inclusione, indicata con è contenuto o incluso nell'insieme se e solo se, per ogni elemento , se appartiene a allora appartiene ad ". E. Appartenenza. Da Wikipedia, l'enciclopedia libera.
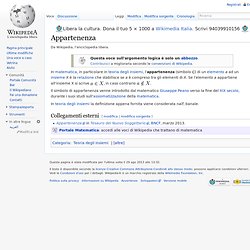
In matematica, in particolare in teoria degli insiemi, l'appartenenza (simbolo , in caso contrario. Quantificatore esistenziale (simbolo) Da Wikipedia, l'enciclopedia libera.
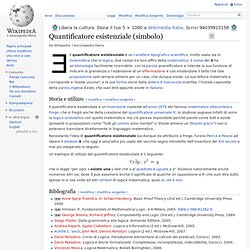
Nonostante l'idea di quantificatore esistenziale sia dunque da attribuire a Frege, furono Peirce e Peano ad ideare il simbolo ∃, che oggi è senz'altro più usato del vecchio segno introdotto dall'inventore del XIX secolo e mai più adoperato in seguito. Un esempio di utilizzo del quantificatore esistenziale è il seguente: (EN) Anne Sjerp Troelstra, H. Schwichtenberg: Basic Proof Theory (2nd ed.). Cambridge University Press, 2000.