

GAMIFICATION URAS. App per prof #51 GEOBOARD (Geometria interattiva) Geometria ed arte: il quadrato - Didatticarte. Cos’avrà mai il quadrato di tanto accattivante?
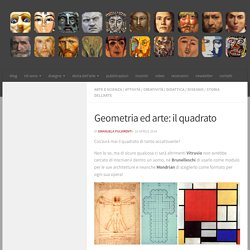
Non lo so, ma di sicuro qualcosa ci sarà altrimenti Vitruvio non avrebbe cercato di inscrivervi dentro un uomo, nè Brunelleschi di usarlo come modulo per le sue architetture e neanche Mondrian di sceglierlo come formato per ogni sua opera! Tanto per cominciare il quadrato è il più regolare tra i quadrilateri: unico poligono che abbia contemporaneamente le caratteristiche del rombo e del rettangolo: quattro lati uguali e perpendicolari. Sempre restando all’ambito scientifico si può estrarre la radice quadrata di un numero o farne il quadrato: si può quindi ricondurre alle proprietà di questa figura piana alcuni procedimenti matematici.
Per questo il quadrato è una figura che esprime perfezione numerica, razionalità, essenzialità. La perfetta regolarità geometrica del quadrato è stata sfruttata sin dai tempi più antichi per strutture murarie o rivestimenti modulari. Ma il quadrato può diventare anche qualcosa di molto più consistente. Il geopiano da costruire con gli alunni - EmmaMetodo. Abbiamo già parlato dell’utilità del geopiano in molte attività di geometria, sia nella primaria che nella secondaria di primo grado; è possibile farne costruire uno individuale a ciascun alunno e, con le dimensioni adeguate, si potrà tenere nel quadernone.
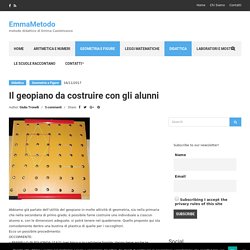
Quello proposto qui sta comodamente dentro una bustina di plastica di quelle per i raccoglitori. Ecco un possibile procedimento: OCCORRENTE: – PANNELLO IN POLIONDA 21X21 (nei brico o in cartolerie fornite. Vanno bene anche le vecchie cartelline di tecnologia e arte) – 49 fermacampioni – Un “dorsetto” – Un foglio a quadretti da 1 cm, di forma quadrata 20×20 – Una matita dura ben temperata Sul foglio quadrato si tracciano i punti dove si andrà a bucare: a un cm dal bordo e ogni tre cm (si ottengono sette file da sette, tot 49 punti) Si fissa con un po’ di scotch il quadrato di carta al centro del pannello di polionda e si procede a bucare con la matita.
Poi si rimuove il foglio a quadretti. Giulia Tronelli View all posts. Osmosi delle Idee » Impara il Teorema di Pitagora giocando. Un semplice gioco di insegna a trovare la misura dell’ipotenusa di un triangolo rettangolo.
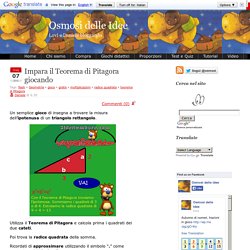
Utilizza il Teorema di Pitagora e calcola prima i quadrati dei due cateti. Poi trova la radice quadrata della somma. Ricordati di approssimare utilizzando il simbolo “.” come separatore dei decimali. Disegnare una piramide con SketchUp. Vediamo come disegnare una piramide a base quadrata utilizzando l’ottimo software gratuito SketchUp.
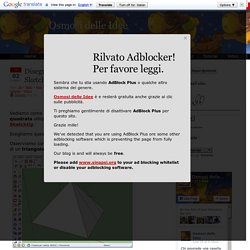
Scegliamo queste misure: lato di base = 6, altezza = 4. Osserviamo come l’apotema e l’altezza facciano parte di un triangolo rettangolo. Aspettato qualche momento che si carichi il filmato e poi usate le frecce verdi per andare avanti o indietro nel tutorial. Articoli che ti possono interessare Volume della piramide con SketchUp Vediamo come calcolare l'area totale e il volume della piramide utilizzando SketchUp. Sono molti giorni che non aggiorniamo il Blog. Esercitati con perimetri e aree. Ripassiamo insieme le formule che ci permettono di calcolare perimetri e aree delle principali figure geometriche piane.
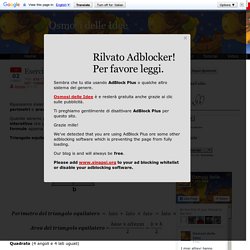
Quando saremo preparati, potremo utilizzare lo strumento interattivo che permette di verificare la comprensione delle formule appena viste. Triangolo equilatero (lati uguali) Quadrato (4 angoli e 4 lati uguali) Rettangolo (4 angoli uguali e lati uguali a coppie) Trapezio (2 lati paralleli) Rombo (4 lati uguali) Romboide (lati e angoli uguali a coppie) Cerchio Ed infine ecco come verificare la propria preparazione, risolvendo i quesiti (con dati numerici sempre nuovi) proposti in questo interattivo Flash.
Articoli che ti possono interessare Dimostrazione geometria piana Dato il trapezio in figura, dimostrare che: DC=AD+BC e l'angolo DOC =90° Dimostrazione 1) Sappiamo, per la nota proprietà, che i segmenti di tangente DT=AD e TC=BC quindi sommando membro a membro...leggi... Questo gioco interattivo ti chiede di trovare la frazione equivalente. Riconosci e usa le coordinate cartesiane. Abbiamo già pubblicato molti articoli con giochi e interattivi dedicati alle coordinate cartesiane.
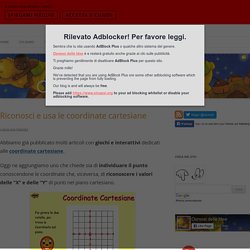
Oggi ne aggiungiamo uno che chiede sia di individuare il punto conoscendone le coordinate che, viceversa, di riconoscere i valori delle “X” e delle “Y” di punti nel piano cartesiano. Nel primo caso dovrete far girare le due rotelline colorate per sorteggiare una coppia di valori, a questo punto individuate il punto corrispondente cliccando nella griglia numerata. Nel secondo esercizio vi comparirà un pallino verde e sarete voi a scrivere i valori esatti delle coordinate cartesiane. Buon Divertimento! Schermo intero p.s. MzswOzEzNDQzMTs2MTQxNTs1NzMzOTsxNDE5NDM7MDsxNDg1MDEzOTM3MDAwOzE5OC4yNy44MS44MTsyYmM5NjdkMThmZGIyMjQwMmYwZjQ0MzkwNGFjZjVmYzsxMTMxNzc7QWRmb3JtUk9OX0FURl83Mjh4OTBfY2FsbGJhY2tVUkw7TEVBREVSQk9BUkRfNzI4WDkwO1JFRElSRUNUO2Q0MWQ4Y2Q5OGYwMGIyMDRlOTgwMDk5OGVjZjg0MjdlOw==
Ritratti ispirati ai graffiti di Barry McGee! Ispirati alle opere di Barry McGee, questi ritratti sono realizzati a collage con carte e cartoncini colorati.
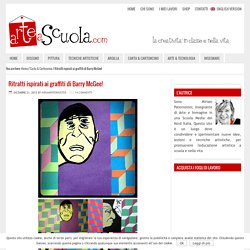
Abbiamo realizzati alcuni ritratti e li abbiamo combinati con superfici in stile “optical art”. I ritratti sono disegnati con pennarelli neri indelebili su cartoncini colorati, con qualche segno bianco disegnato con il “bianchetto”. La cosa più divertente è stata convincere gli alunni che i ritratti potevano essere anche molto brutti e non necessariamente somiglianti ai volti delle fotografie, pieni di rughe e con strane espressioni, nello stile dei graffiti di Barry McGee! Punto retta semiretta segmento.