

Le cinquième postulat – Mathématiques et Antiquité. Images des mathématiques. Les ouvrages d’Euclide Euclide est pour nous le nom de la personne à laquelle sont attribués des ouvrages mathématiques écrits en grec ancien, lesquels nous ont été transmis par des manuscrits qui ne remontent pas plus haut que le IXe siècle.
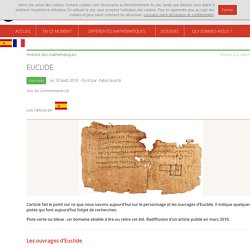
Cette affirmation, quoique passablement contournée, peut paraître une lapalissade, mais les réserves qu’elle formule de façon implicite n’ont jamais été monnaie courante parmi les historiens des mathématiques. Nous allons d’abord examiner les ouvrages géométriques qu’on attribue à Euclide, pour nous tourner ensuite sur les réserves qu’on entend aujourd’hui formulées au sujet du personnage lui-même. Dans un troisième temps, on introduira quelques pistes récentes de recherche sur les ouvrages attribués à Euclide. Euclide était, dès l’antiquité, désigné comme « l’homme des Éléments », selon le titre de son traité le plus connu. Une première partie (livres I-IV) expose bien les fondements de la géométrie plane et certaines de ses applications. Th or me de Pythagore selon Euclide. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Le célèbre théorème de Pythagore affirme que dans un triangle ABC rectangle en A (donc d'hypoténuse BC) : Pythagore apporta une preuve de "son théorème", mais voici comment Euclide le démontre dans ses Eléments (premier Livre, proposition 47) : Les triangles FGB et GBC ont même aire : ils ont un côté commun [BG] et une même hauteur relative à ce côté : FG.

D'autre part les triangles GBC et ABD sont isométriques car ils ont un angle de même mesure (90° + ^B) et les côtés de cet angle de même mesure : [BG] et [BC] d'une part, [BA] et [BD] d'autre part). Enfin, l'aire de ABD est la moitié de BD x DK, aire du rectangle BHKD. Résumons : aire FGBA = 2 x aire FGB = 2 x aire GBC = 2 x aire ABD = aire BHKD On raisonnerait de même afin de prouver que l'aire de ACJL est celle de HCEK. BC2 = AB2+ AC2 et B'C2 = AB'2+ AC2,
Géométrie euclidienne élémentaire. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges A l'origine, la géométrie est la mesure de la Terre : en grec, gê = terre et metron = mesure.

En premier lieu, Euclide définit les objets usuels de la géométrie plane : point : ce dont la partie est nulle; ligne (finie) : longueur sans largeur dont les extrémités sont des points; droite : ligne qui est également (de manière égale) placée entre ses points; droites (distinctes) parallèles d'un même plan : droites qui, prolongées indéfiniment d'un côté ou de l'autre, ne se rencontrent pas. » Euclide ne définit pas le segment par un terme spécifique : il parle de droite finie (limitée de part et d'autre). L'AXIOMATIQUE - Les Éléments d'Euclide.
EUCLIDE. Naissance: vers 325 av.
J. -C., Grèce - Mort : vers 265 av. J. -C., Alexandrie. Sommaire. Euclide, personnage mystérieux.Les Eléments, approche historique et historicité.Les Eléments, un texte apocryphe.La première oeuvre imprimée.Vers un souci de rigueur historique : Le codex Vaticanus.Les Eléments.Description de l'ouvrage.Le premier Livre.Définitions.DEMANDES ou POSTULATS.Le 5ème Postulat d'EUCLIDE et les géométries non euclidiennes.Notions communes.3b5. 1. La personnalité d'Euclide nous est quasiment inconnue. Proclus de Lycie, dit « le Diadoque » (littéralement, "celui par qui le sceptre est transmis"), vécut au 5ème siècle, sans doute de 412 à 485.
Qu'« Euclide n'est pas beaucoup plus jeune que les mathématiciens du 4ème siècle avant J. Euclide le père de la géometrie. Biographie de Euclide d'Alexandrie. Si l'on devait se contenter de rédiger une notice biographique de la vie d'Euclide, alors elle serait très courte : on ne sait rien, ou presque, de celui que l'on peut considérer comme le plus grand enseignant de mathématiques de l'histoire.

Tout juste pense-t-on qu'il étudia à l'école des successeurs de Platon à Athènes, avant de s'établir à Alexandrie, sous l'invitation de Ptolémée I. Mais comme ces suppositions reposent sur des écrits de Proclus qui datent de 9 siècles après Euclide, on conçoit qu'elles sont peu fiables! Ce que l'on connait bien d'Euclide, ce sont les ouvrages qui nous sont parvenus signés de son nom, parmi lesquels Données, et surtout les 13 volumes des Éléments. Du reste, on ne sait pas trop quel est le rapport exact entre Euclide et les connaissances qu'il expose. Il semble bien qu'aucun des résultats des Eléments ne soit dû à Euclide, et que son oeuvre consiste en une remise à plat de différentes notions exhibées par des mathématiciens divers.