

Prime Integer Observatory. This application illustrates the notion of an integer? S factors, and of the related property of integers called primeness, or primality. An integer is called prime if it is the product of only one distinct pair of integers. freeware by Atomic Concepts Software This application illustrates the notion of an integer? S factors, and of the related property of integers called primeness, or primality. Mathematics , math , factor , factorization , integer , Prime , factors Program Release Date: Program Release Status: New Release Languages: English Operating Systems: Win98 , WinME , WinNT 3.x , WinNT 4.x , WinXP , Windows2000 , Windows2003 , Windows Vista Starter , Windows Vista Home Basic , Windows Vista Home Premium , Windows Vista Business , Windows Vista Enterprise , Windows Vista Ultimate Program Install Support: No Install Support.
Home. The Prime Page's Links++: visualization/via_images. Ulam spiral. Do you see any pattern in this graph?
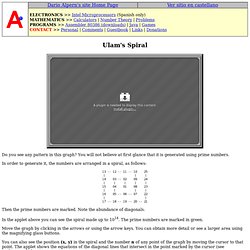
You will not believe at first glance that it is generated using prime numbers. In order to generate it, the numbers are arranged in a spiral, as follows: Then the prime numbers are marked. Note the abundance of diagonals. In the applet above you can see the spiral made up to 1014. Move the graph by clicking in the arrows or using the arrow keys. You can also see the position (x, y) in the spiral and the number n of any point of the graph by moving the cursor to that point. Move the center by typing a new number (up to 14 digits) in the left input box and press the return key. Change the starting number in the center of the spiral by typing a new number (up to 14 digits) in the right input box and press the return key.
The formula that gives the numbers in the diagonal lines can be expressed using quadratic polynomials. When the quadratic polynomial cannot be factorized, then its diagonal will contain primes. A visual Sieve for Prime Numbers. Primenumbers. Radiant Prime. That is all I require: Building Numbers. Caution: Distraction ahead.
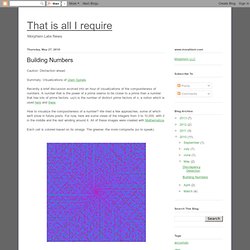
Summary: Visualizations of Ulam Spirals. Recently a brief discussion evolved into an hour of visualizations of the compositeness of numbers. A number that is the power of a prime seems to be closer to a prime than a number that has lots of prime factors. ω(n) is the number of distinct prime factors of n, a notion which is used here and there. How to visualize the compositeness of a number? We tried a few approaches, some of which we'll show in future posts. Each cell is colored based on its omega. A variation, this time showing the structure of each number: Each number is represented by a square that depicts the number's prime factorization. Color is given by the size (so to speak) of the largest prime in the factorization.
But we didn't like those as much. Here are some closer views of the 2D representations. If there's any interest, we can make our PDF versions available. A wall-sized print would be interesting. Frequency of Primes. Frequency of Primes Tags: prime , primes , visualization Categories: Color Theory , Data Visualization , Education , Featured , Programming Project Summary How often do prime numbers occur within a list of integers?
Is there any pattern? Several Pratt students study a 48" x 96" print of one prime number study. Developing a Color System Looking at a matrix of integers in which the prime numbers are highlighted, the gap in between any two primes forms a block of space. As the intervals get larger, the hue of the color transitions from blue to purple to red to green. Prime Factorization Graph. Prime number. Prime Sieve. Graph of cos(n'th prime number).gif (GIF Image, 4096x4096 pixels) Sqrt(2) vs. Prime Numbers. Prime Integer Observatory: Visualization of integer factorizations as a scrollable table. Primal Chaos. The image shows a random multiple of 6 at "6k".
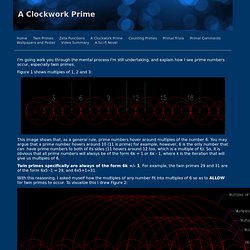
In order to have twin primes we cannot have any circle intersecting adjacently to 6k (obviously). Let's see how this happens: Please note that the reason I'm only using prime numbers for this is because we only need prime numbers. For example, the 9 is not needed because it is a multiple of 3 (3 is prime and can only fall on 6k). Same with 15, 21, 27 and so on (which are also multiples of 3). -Multiples of 3 can only fall on 6k. -Multiples of 5 can fall on 6k, 6k-2, 6k-3.