

9411216.pdf. Co.combinatorics - Tiling A Rectangle With A Hint of Magic. Here's a a famous problem: There are a number of proofs of this result (14 proofs in this particular paper).
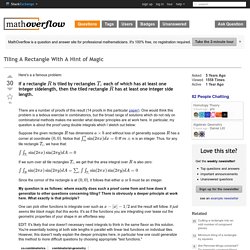
One would think this problem is a tedious exercise in combinatorics, but the broad range of solutions which do not rely on combinatorial methods makes me wonder what deeper principles are at work here. In particular, my question is about the proof using double integrals which I sketch out below: Suppose the given rectangle has dimensions and without loss of generality suppose has a corner at coordinate . Notice that iff is an integer. If we sum over all tile rectangles , we get that the area integral over is also zero: Since the cornor of the rectangle is at , it follows that either or must be an integer. My question is as follows: where exactly does such a proof come from and how does it generalize to other questions concerning tiling? One can pick other functions to integrate over such as and the result will follow. Tilings. 82_04_tiling.pdf. Easier Fibonacci Number puzzles. All these puzzles except one (which??)

Have the Fibonacci numbers as their answers. So now you have the puzzle and the answer - so what's left? Just the explanation of why the Fibonacci numbers are the answer - that's the real puzzle!! Puzzles on this page have fairly straight-forward and simple explanations as to why their solution involves the Fibonacci numbers;. Puzzles on the next page are harder to explain but they still have the Fibonacci Numbers as their solutions. 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ..More.. Fibonacci numbers and Brick Wall Patterns If we want to build a brick wall out of the usual size of brick which has a length twice as long as its height, and if our wall is to be two units tall, we can make our wall in a number of patterns, depending on how long we want it: There's just one wall pattern which is 1 unit wide - made by putting the brick on its end.
Penrose tiling. A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles.
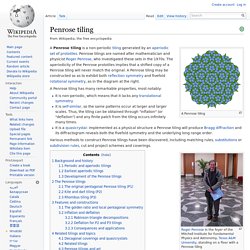
Penrose tilings are named after mathematician and physicist Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right. A Penrose tiling has many remarkable properties, most notably: It is non-periodic, which means that it lacks any translational symmetry.It is self-similar, so the same patterns occur at larger and larger scales. Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions or subdivision rules, cut and project schemes and coverings. Background and history[edit] Periodic and aperiodic tilings[edit] Figure 1.
Earliest aperiodic tilings[edit] Robinson's six prototiles Figure 2. Notes[edit] Packing problems. This article is about geometric packing problems.
For numerical packing problems, see Knapsack problem. Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap. In a packing problem, you are given: 'containers' (usually a single two- or three-dimensional convex region, or an infinite space)A set of 'objects' some or all of which must be packed into one or more containers. Usually the packing must be without overlaps between goods and other goods or the container walls.
Packing infinite space[edit] . . Fast Optimizing Rectangle Packing Algorithm for Building CSS Sprites. Introduction This article describes a fast algorithm to pack a series of rectangles of varying widths and heights into a single enclosing rectangle, with no overlap and in a way that minimizes the amount of wasted space in the enclosing rectangle.
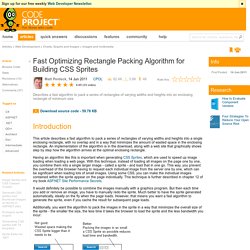
An implementation of the algorithm is in the download, along with a web site that graphically shows step by step how the algorithm arrives at the optimal enclosing rectangle. Having an algorithm like this is important when generating CSS Sprites, which are used to speed up image loading when loading a web page. With this technique, instead of loading all images on the page one by one, you combine them into a single larger image - called a sprite - and load that in one go. This way, you prevent the overhead of the browser having to request each individual image from the server one by one, which can be significant when loading lots of small images.
It would definitely be possible to combine the images manually with a graphics program. Contents.