

GeoGebra. Radiante. Da Wikipedia, l'enciclopedia libera.
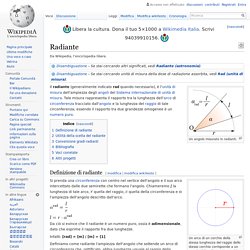
Un angolo misurato in radianti. Definizione di radiante[modifica | modifica wikitesto] Un arco di un cerchio della stessa lunghezza del raggio dello stesso cerchio corrisponde a un angolo di 1 radiante. Un cerchio intero corrisponde a un angolo di 2π radianti. Alcuni angoli misurati in radianti Si prenda una circonferenza con centro nel vertice dell'angolo e il suo arco intercettato dalle due semirette che formano l'angolo. La lunghezza di tale arco, quella del raggio, quella della circonferenza e l'ampiezza dell'angolo descritto dall'arco. Da ciò si evince che il radiante è un numero puro, ossia è adimensionale, dato che esprime il rapporto fra due lunghezze. Infatti: [rad] = [m] / [m] = [1]. Definiamo come radiante l'ampiezza dell'angolo che sottende un arco di circonferenza che, rettificato, abbia lunghezza uguale al raggio della circonferenza stessa. Essendo la lunghezza della circonferenza pari a e il raggio lungo , l'angolo di un cerchio equivale a ovvero.
Trucchetti Matematica. Logica. Apprendere la matematica - corsi. Matematici & Storia della Matematica. Analisi matematica. Matematica, sub-folder. Umorismo matematico. Wiki, matematica & logica. BASE Cinque - Appunti di Matematica ricreativa. Matematicamente.it. Math.it - didattica e divulgazione della matematica. Paradosso dell'area scomparsa - Missing square puzzle. Il paradosso di Achille e la tartaruga rivisitato - Riflessioni sulle Scienze di Alberto Viotto. Di Alberto Viotto indice articoli Il paradosso di Achille e la tartaruga rivisitato.
Ottobre 2008 Zenone di Elea La soluzione classica La visione della meccanica quantistica L’indeterminazione Quando Achille sta per raggiungere la tartaruga Zenone aveva ragione Zenone di Elea Tutti i lettori avranno certamente sentito parlare del paradosso di “Achille e la tartaruga”, proposto attorno al 500 avanti Cristo dal filosofo greco Zenone di Elea. Il velocissimo Achille ed una tartaruga si sfidano ad una gara di corsa. La soluzione classica La soluzione più comune di questo paradosso analizza la somma degli infiniti intervalli temporali che abbiamo considerato. Da un punto di vista matematico questa somma di infiniti termini converge (è sempre minore di uno) ed il suo limite è uno.
Questa spiegazione lascia però in qualche modo insoddisfatti. Quando Achille sta per raggiungere la tartaruga Che cosa succede, però, quando Achille sta per raggiungere la tartaruga? Alberto Viotto. Paradosso di Achille di Zenone - Approfondimenti. Giochi matematici. Quando Achille si trova in Ao la tartaruga è in To.
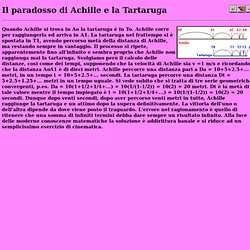
Achille corre per raggiungerla ed arriva in A1. La tartaruga nel frattempo si è spostata in T1, avendo percorso metà della distanza di Achille, ma restando sempre in vantaggio. Il processo si ripete, apparentemente fino all'infinito e sembra proprio che Achille non raggiunga mai la tartaruga. Svolgiamo però il calcolo delle distanze, cosi come dei tempi, supponendo che la velocità di Achille sia v =1 m/s e ricordando che la distanza AoA1 è di dieci metri. Achille percorre una distanza pari a Da = 10+5+2.5+... metri, in un tempo t = 10+5+2.5+... secondi. Mathematical Software. Wolfram MathWorld: The Web's Most Extensive Mathematics Resource. Wolfram Alpha. Da Wikipedia, l'enciclopedia libera.
Il titolo di questa voce non è corretto per via delle caratteristiche del software MediaWiki. Il titolo corretto è Wolfram|Alpha. Wolfram|Alpha è un motore computazionale di conoscenza[1] che interpreta le parole chiave inserite dall'utente e propone direttamente una risposta invece che offrire una lista di collegamenti ad altri siti web. L'autore di questo strumento, attivato il 18 maggio 2009, è lo scienziato e matematico britannico Stephen Wolfram[2], conosciuto per aver sviluppato il software Mathematica. Wolfram|Alpha consiste di oltre 5 milioni di righe di codice simbolico di alto livello Mathematica, 50.000 algoritmi, è installato su supercomputer cluster, fa uso estensivo della tecnologia parallela e grid.
Esempi di utilizzo[modifica | modifica sorgente] Matematica[modifica | modifica sorgente] Biologia[modifica | modifica sorgente] Bioinformatica[modifica | modifica sorgente] Software di matematica simili a wolfram alpha - Leggi argomento. Mmm...no, mi spiace A parte Derive (peggio) e Wolfram Alpha (meglio, ma...) non conosco programmi che mostrino passaggio per passaggio lo svolgimento dell'esercizio.
Però, se me lo permetti, ti vorrei dare un consiglio Personalmente ho "abbandonato" i software da circa un'annetto, poco prima di dare Analisi I, essendomi reso conto della loro "stupidità", nonchè della mia nell'affidarmi a loro...ormai li uso pochissimo, quasi a mo' di calcolatrice, specie quando devo fare noiosissimi conti negli esercizi di Fisica Mi spiego. Prendiamo Wolfram Alpha ad esempio; se quello che cerchi è lo svolgimento passo passo d'un esercizio, affidarsi a questo programma, secondo me, non è l'ideale. 9 limiti su 10 li risolve con De L'Hopital! Se sono degli esercizi svolti che cerchi, in rete ce ne sono a bizzeffe, e personalmente ti consiglio di preferire questi ai software.
Notte Giuseppe. Math Fonts. Hyperlink. Matematica & Logica. Hyperlink. Mathematics.