

Simulation du Grand Oral du Bac - Spécialité Maths - LLCE. L'histoire d'Alan Turing ou presque... Enigma (machine) Enigma, une machine de chiffrement électromécanique à cylindres ; la version ci-dessus est un modèle militaire suisse, avec une console de lecture supplémentaire.
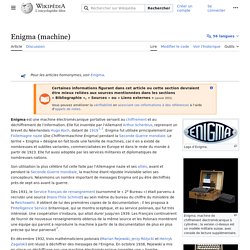
Enigma est une machine électromécanique portative servant au chiffrement et au déchiffrement de l'information. Elle fut inventée par l'Allemand Arthur Scherbius, reprenant un brevet du Néerlandais Hugo Koch, datant de 1919[1],[2]. Enigma fut utilisée principalement par les Allemands (Die Chiffriermaschine Enigma) pendant la Seconde Guerre mondiale.
Le terme Enigma désigne en fait toute une famille de machines, car il en a existé de nombreuses et subtiles variantes, commercialisées en Europe et dans le reste du monde à partir de 1923. Elle fut aussi adoptée par les services militaires et diplomatiques de nombreuses nations. Son utilisation la plus célèbre fut celle faite par l'Allemagne nazie et ses alliés, avant et pendant la Seconde Guerre mondiale, la machine étant réputée inviolable selon ses concepteurs. Le réflecteur, et et. Alan Turing - Enigma, ordinateur et pomme empoisonnée - LPPV.05 - e-penser. Diapos turing brest. Cryptanalyse d'Enigma. Avant le début de la guerre, le mathématicien polonais Marian Rejewski élabore la première cryptanalyse, fondée sur une redondance : le mode de chiffrement de la clef choisie par le chiffreur était répété dans le préambule du message.
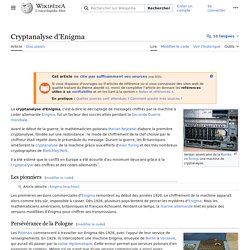
Durant la guerre, les Britanniques améliorent la cryptanalyse de la machine grâce aux efforts d'Alan Turing et des très nombreux cryptographes de Bletchley Park. Il a été estimé que le conflit en Europe a été écourté d'au minimum deux ans grâce à la cryptanalyse des chiffres et des codes allemands[1]. Les pionniers[modifier | modifier le code] Persévérance de la Pologne[modifier | modifier le code] Machine exposée à Varsovie, Pologne Les Polonais commencent à travailler sur Enigma dès 1928, avec l'appui de leur service de renseignements. Marian Rejewski, mathématicien polonais de 27 ans, découvre alors un moyen mathématique de retrouver ces deux paramètres essentiels. Les chaînes[modifier | modifier le code] Le nombre de chaînes possibles est 105 456. TPEenigma. La partie des petits scientifiques - enigma-tique. En quoi les Mathématiques ont-elles été essentielles dans le fonctionnement d'Enigma ?

I. Descriptif Le principe de fonctionnement : En appuyant sur une touche (A), le courant passe par les 3 rotors, arrive au réflecteur qui le renvoie dans les rotors et envoie le signal crypté (C). LA MACHINE ENIGMA. Importance historique « Les mathématiciens ont gagné la guerre !
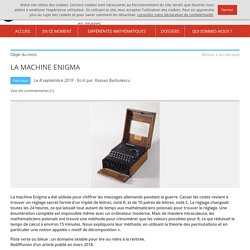
» - résonne une voix au début du film « Un homme d’exception ». Cette phrase peut surprendre car les codes secrets ne sont pas restés dans la mémoire collective à cause du caractère secret de ces travaux, classés secret défense jusqu’en 1995. Conçue par l’ingénieur Arthur Scherbius en 1923, la machine Enigma a été commercialisée à toute personne qui voulait garder la confidentialité de ses communications, par exemple aux sociétés industrielles. Après un échec commercial cuisant, Scherbius a décidé en 1926 de vendre la machine à l’armée allemande, sans anticiper qu’elle allait servir aux nazis. Grâce aux informations procurées par les services secrets Français en 1931, trois mathématiciens polonais, Marian Rejewski, Jerzy Różycki et Henryk Zygalski, ont réussi l’exploit de casser les codes d’Enigma.
Les mathématiques pendant la seconde guerre mondiale. Été 1940.
La guerre semble avoir choisi son camp. La Pologne, la France ont capitulé. La Grande-Bretagne résiste, mais elle dépend, pour la moitié à peu près de son approvisionnement en matières premières, des importations maritimes. Or, dans les mers, les sous-marins allemands, les redoutables U-Boot, font régner la terreur, coulant de nombreux navires. Ils attaquent de nuit, en meutes.
#43 - Pêche miraculeuse d'une machine ENIGMA. L'histoire d'Alan Turing ou presque... Fonctionnement – Réplique Enigma. Dans la partie histoire, nous avons vu qu’un chiffrage par substitution n’est pas suffisamment sur.

Si la quantité de texte intercepté est assez important le code est facilement cassable. Hors-série 2 (Conférence Alkindi ft. Razvan Barbulescu) Cryptographie - partie 1 : chiffrement de César. Cryptographie - partie 2 : chiffrement de Vigenère. Cryptographie - partie 3 : la machine Enigma et les clés secrètes. COMMENT LES MATHÉMATIQUES ONT INVESTI LA CRYPTOLOGIE (1) La cryptologie – du grec, Kryptos, caché – associe deux domaines : la cryptographie, qui élabore ces procédures, et la cryptanalyse, qui travaille au contraire à les déjouer [1].

Longtemps fondée sur une analyse quantitative et qualitative du langage écrit, elle s’est progressivement imprégnée de mathématiques jusqu’à modifier sa nature et ses pratiques, surtout depuis que la mécanisation a décuplé les potentialités des procédures de chiffrement, et bloqué du même coup les possibilités d’un décryptement manuel. Cette première partie concerne la période où les outils principaux de chiffrement et de décryptement venaient de l’analyse du langage. Néanmoins, depuis les érudits arabes, des mathématiques furent localement introduites pour le décryptement, mais les différentes techniques envisagées ont lentement évolué, en raison du secret entourant ces pratiques. COMMENT LES MATHÉMATIQUES ONT INVESTI LA CRYPTOLOGIE (2) Les desiderata de Kerckhoffs Au-delà des premiers rapprochements avec les mathématiques, c’est la naissance du télégraphe qui transforme radicalement la portée du secret.

Après une démonstration d’une transmission Paris-Lille en moins de six heures, la Convention adopte dès 1793 le télégraphe optique des frères Chappe. LYC70. Alan Turing, un grand décodeur. Machine de Turing expérimentale. Probléme de la décision : Son remarquable article à On Computable Numbers, with an Application to the Entscheidungsproblem à (1936), répond à un problème posé par Hilbert dans les théories axiomatiques, le problème de la décision (Entscheidungsproblem) : est-il possible de trouver une méthode "effectivement calculable" pour décider si une proposition est démontrable ou non.
Pour montrer que cela n'est pas possible, il faut caractériser ce qu'est un procédé effectivement calculable.Turing le fait en imaginant, non une machine matérielle, mais un "être calculant", qui peut être indifféremment un appareil logique trés simple ou un humain bien discipliné appliquant des régles comme le faisaient les employés des bureaux de calcul à l'époque. Histoire de l'informatique. Criptografía - Máquina Enigma, funcionamiento detallado. Gambling with Secrets: Part 1/8 (What is Cryptography?) The Enigma Code. Flaw in the Enigma Code - Numberphile. Machine de Turing, l'ancêtre de l'ordinateur par Thierry Delattre lors des journées JAIME 2021. LA MACHINE DE TURING. Un épisode de la série les 5 minutes Lebesgue Le 29 août 2021 - Ecrit par Collectif Les 5 minutes Lebesgue S’abonner aux 5 minutes Lebesgue : Les 5 minutes Lebesgue sont une série vidéo proposée par le Centre Henri Lebesgue.
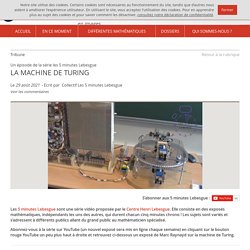
Elle consiste en des exposés mathématiques, indépendants les uns des autres, qui durent chacun cinq minutes chrono ! Les sujets sont variés et s’adressent à différents publics allant du grand public au mathématicien spécialisé. LA MACHINE DE TURING (1) Alan Turing a publié en 1936 un article intitulé « On computable numbers, with an application to the Entscheidungsproblem ».
Il y décrit un dispositif que l’on appelle « la machine de Turing », et que l’on peut représenter par le schéma suivant : La machine est composée de : un ruban infini comportant des cases dans lesquelles sont écrits des symboles une tête de lecture/écriture qui peut : lire le symbole écrit dans la case au-dessus ;écrire ou non un autre symbole dans cette case ;se déplacer d’une case à gauche ou à droite ;changer d’état ; LA MACHINE DE TURING (2) Dans l’article « La machine de Turing (1) », nous avons vu la description générale du système et comment les lignes des tables des transitions représentent les étapes de l’exécution d’un algorithme. Nous avons appliqué cela aux positionnements de la tête de lecture/écriture et aux traitements de base des chaînes de caractères. Si nous voulons nous placer sur un plan plus général et théorique, nous dirons que notre machine de Turing est constituée de : Ces six points constituent la base à retenir pour la suite de ces articles.
Pour commencer, nous allons voir une méthode pour représenter graphiquement les tables des transitions sous la forme de diagrammes. Les schémas visuels permettent souvent de mieux comprendre l’enchaînement des étapes dans le déroulement d’un processus. La machine de Turing : tout ne se calcule pas ! Machine de Turing. Vue d’artiste d’une machine de Turing : un ruban infini muni d'une tête de lecture/écriture. La machine dispose également d'une table de transition, non représentée sur l'image. En informatique théorique, une machine de Turing est un modèle abstrait du fonctionnement des appareils mécaniques de calcul, tel un ordinateur. Ce modèle a été imaginé par Alan Turing en 1936, en vue de donner une définition précise au concept d’algorithme ou de « procédure mécanique ». Il est toujours largement utilisé en informatique théorique, en particulier dans les domaines de la complexité algorithmique et de la calculabilité.
À l'origine, le concept de machine de Turing, inventé avant l'ordinateur, était censé représenter une personne virtuelle exécutant une procédure bien définie, en changeant le contenu des cases d'un ruban infini, en choisissant ce contenu parmi un ensemble fini de symboles. Définition[modifier | modifier le code] Un ruban infini divisé en cases consécutives. Où : , alors elle écrit. Machines de Turing. A Turing Machine Overview. Alan Turing, vous avez dit calculs, par Marie Claude Gaudel - Replay du 17/02/2020.
Cryptographie.