

Histoire de la trigonométrie. Histoire de la Trigonométrie. VERY HARD South Korean Geometry Problem (CSAT Exam) Trucs mnémotechniques en trigonométrie. Les moyens mnémotechniques pour mémoriser plus facilement les formules de sinus, cosinus et tangente en trigonométrie ne manquent pas !
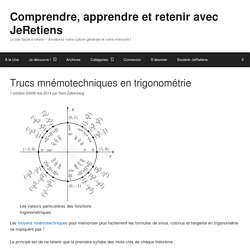
Le principe est de ne retenir que la première syllabe des mots-clés de chaque théorème : Cosinus = côté Adjacent sur l’Hypoténuse » devient cosadjip ou “CAHier” Sinus = côté Opposé sur l’Hypoténuse » devient sinopip ou “SOHo” Tangente = côté Opposé sur côté Adjacent » devient tangopaj ou “TOAst” Identité trigonométrique. Une identité trigonométrique est une relation impliquant des fonctions trigonométriques, vérifiée pour toutes les valeurs possibles des variables intervenant dans la relation.
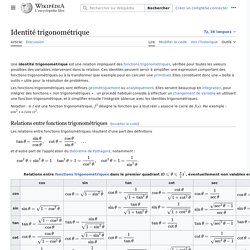
Ces identités peuvent servir à simplifier une expression comportant des fonctions trigonométriques ou à la transformer (par exemple pour en calculer une primitive). Elles constituent donc une « boîte à outils » utile pour la résolution de problèmes. Notation : si ƒ est une fonction trigonométrique, ƒ2 désigne la fonction qui à tout réel x associe le carré de ƒ(x). Les algorithmes cachés dans les calculatrices : TRIGONOMETRIE. Les formules de trigonométrie, facile! La trigonométrie, c’est l’une des bases fondamentales qu’il faut maîtriser en maths, elle est partout !
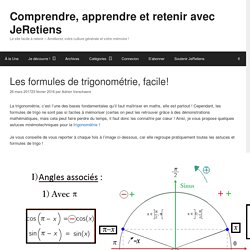
Cependant, les formules de trigo ne sont pas si faciles à mémoriser (certes on peut les retrouver grâce à des démonstrations mathématiques, mais cela peut faire perdre du temps, il faut donc les connaître par cœur ! Ainsi, je vous propose quelques astuces mnémotechniques pour la trigonométrie ! Je vous conseille de vous reporter à chaque fois à l’image ci-dessous, car elle regroupe pratiquement toutes les astuces et formules de trigo !
I) Angles associés : 1) Pour déterminer les angles associés à π, il faut toujours avoir le cercle trigonométrique en tête (en le reproduisant plusieurs fois, il est vite mémorisé), ensuite il faut considérer que l’axe des abscisses correspond au cosinus et que l’axe des ordonnées correspond au sinus. II) Formules de base : De même, pour sinus qui est égal au côté opposé sur l’Hypoténuse, on a : “sinopip” Math.ing : les angles et leur mesure. Trigonométrie. (trigonométrie) La géométrie est la discipline mathématique ayant pour objet l'étude rigoureuse des espaces et des formes.

(Larousse) Dernière mise à jour de ce chapitre: 2017-12-31 17:59:07 | {oUUID 1.786} Version: 3.2 Révision 11 | Avancement: ~100% vues depuis le 2012-01-01: 62'472 La trigonométrie fait partie intégrante de la science de la géométrie. 1C Theme 7. 2C Theme 11. GEOGEBRA in html-Daniel MENTRARD. BOB. Souris Lilliputienne. Cours trigonometrie.
Le radian. Radian Roger Cotes. Sinus alpha plus béta. La loi des sinus. Preuve de la loi des Cosinus. Al Kashi) Histoire de la Trigonométrie. Activités autour de la trigonométrie. UN GRAND REMERCIEMENT AUX WEBMASTERS DES SITES SUIVANTS POUR LEURS INFORMATIONS ET LEURS IMAGES « LIBRES » sans brevet : Merci aux enseignants de l’académie de Clermont-Ferrand pour leur excellente banque de données mise à la disposition des enseignants, tout particulièrement pour l’article sur la trigonométrie de Jean Philippe Darras. Merci à Daniel Joly pour son bel article sur les ondes radio et pour l’autorisation de publier une image de son site. Un grand merci à Wikimedia Commons pour toutes ces images libres qui m’ont permis de réaliser le diaporama sur l’histoire de la trigonométrie.
Merci à Wikipédia pour l’histoire des mathématiciens arabes. Merci au webmaster de Chronomath pour son excellent site. 1. Activité de découverte 2. Cette figure permet de faire apparaître la courbe sinusoïdale à partir d’un cercle : Créé avec GeoGebra 3. JPEG et DCT. Bloc initial de pixelsBloc reconstitué Cliquez sur les images de base pour les sélectionner, et observez l'évolution du bloc reconstitué.

Comparez le bloc reconstitué quand toutes les images de base sont sélectionnées, et lorsque on retire celles en bas à droite. Trigo sans pleurs. 13 Legrand exo. Formulaire trigo.
[UT#43] □ Le formulaire de trigonométrie. Formulaire de trigonométrie hyperbolique. Cours [Trigonométrie circulaire - Trigonométrie hyperbolique] Free Math Worksheets (pdfs) with answer keys on Algebra I, Geometry, Trigonometry, Algebra II, and Calculus. Trigonométrie sphérique. Triangle sphérique[modifier | modifier le code] La somme des angles d'un triangle sphérique peut varier entre 180 et 540° (entre π et 3π radians)[a],[1].
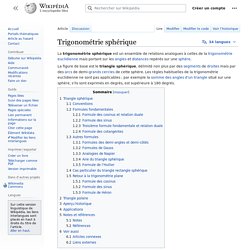
Formules fondamentales[modifier | modifier le code] Triangle sphérique avec ses grands cercles et ses angles au centre (l’angle a s’identifie à BC si on suppose le rayon égal à 1) Conventions[modifier | modifier le code] On considère trois points A, B et C sur une sphère comme représentés par la figure ci-contre, ainsi que les arcs de grands cercles qui les relient. ) l'angle du triangle au sommet A, et de façon analogue pour les autres sommets.
. , etc. Spherical trigonometry. The origins of spherical trigonometry in Greek mathematics and the major developments in Islamic mathematics are discussed fully in History of trigonometry and Mathematics in medieval Islam.
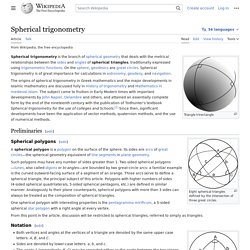
The subject came to fruition in Early Modern times with important developments by John Napier, Delambre and others, and attained an essentially complete form by the end of the nineteenth century with the publication of Todhunter's textbook Spherical trigonometry for the use of colleges and Schools.[1] Since then, significant developments have been the application of vector methods, and the use of numerical methods. Preliminaries[edit] Eight spherical triangles defined by the intersection of three great circles.
Formulaire de trigonométrie sphérique. When teaching precalc helps me invent integral magic. Fonction secante & cosécante. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Les fonctions sécante (sec) et cosécante (cosec ou csc) ont été initiées par Abu l'Wafa.

Leurs appellations sont dues à Frénicle de Bessy et les notations actuelles à Oughtred. I - Fonction sécante Nom de la fonction : sécante, abrégé en sec : sec(x) = 1/cos(x). C'est une fonction transcendante. Autres thèmes de Trigonométrie. Trigonométrie circulaire - Trigonométrie hyperbolique. Fonction hyperbolique. Une demi-droite passant par l'origine intersecte l'hyperbole d'équation x2 – y2 = 1 au point (cosh a, sinh a), où a est le double de l'aire algébrique de la surface délimitée par la demi-droite, l'hyperbole et l'axe des x.
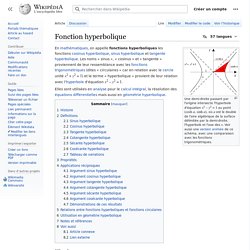
Voir aussi une version animée de ce schéma, avec une comparaison avec les fonctions trigonométriques. Histoire[modifier | modifier le code] Hyperbole Trigonométrique. Détermination de la fonction réciproque du cosinus hyperbolique ARGCH et sa dérivée ARGCH' Détermination de la fonction réciproque de la tangente hyperbolique ARGTH et sa dérivée ARGTH' Détermination de la fonction réciproque du sinus hyperbolique ARGSH et sa dérivée ARGSH' Incollable sur les primitives (à la québécoise) Pourquoi c'est rond ? Brachistochrone et chaînette.